Что такое основание куба? Это плоская фигура, которая образует его нижнюю часть, а точнее — одну из его шести граней. Как можно догадаться, основание куба является плоским и прямоугольным. Это означает, что у всех четырех сторон основания прямые углы. Куб — одно из самых простых геометрических тел, который имеет множество интересных свойств и применений. Например, куб может быть использован для построения трехмерного графика или сравнения объемов различных объектов. Давайте рассмотрим подробнее основание куба и его особенности.
Определение куба
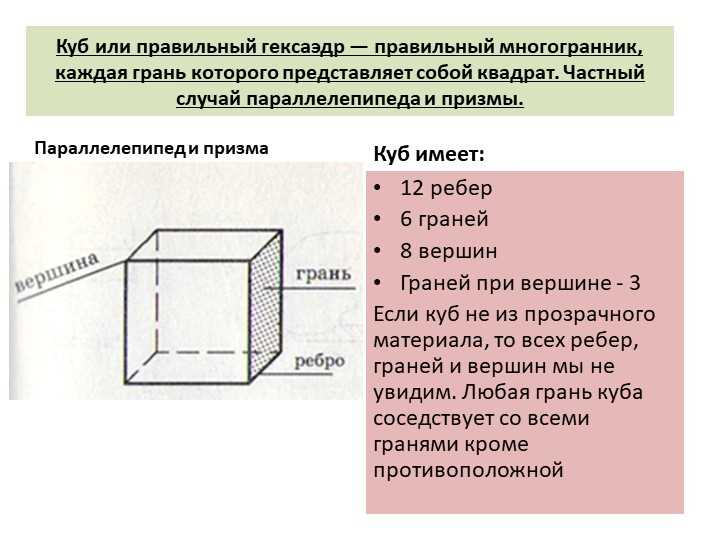
Вообрази себе куб. Ты думаешь, что это всего лишь некий трёхмерный квадрат? Но нет, куб — это куда больше, это маленький мир в трёх измерениях. Необыкновенная симметрия и точность, способные окутать тебя, как волшебная пелена. Ребра куба суть отрезки, соединяющие две вершины, а чудесные грани — это шесть квадратов.
Ты знаешь, что куб имеет несколько осей симметрии? Представь себе, что если ты перевернешь его по некоторым из этих осей, получится то же самое изображение. Потрясающе, не правда ли? Куб — это такая удивительная и хитрая фигура, которая сама строит перед тобой забавные загадки и головоломки.
У куба есть еще кучка замечательных свойств. К примеру, все его грани и ребра равны между собой. А это означает, что куб имеет равные стороны, а значит, и равные углы! Магия, не так ли?
А знаешь ли ты, сколько вершин имеет куб? Аж восемь! И каждая из них является центром кубической симметрии. Представь, как легко можно к этим точкам прикасаться, и каждая даст радужный ответ на твою нежную просьбу.
Но знаешь, что самое интересное? А то, что куб — это всего лишь начало! Вселенная геометрии заполняется множеством других фигур, у которых есть свои уникальные свойства и тайны. И каждая из них может стать твоим верным спутником в путешествии по бесконечному пространству мира математики.
Геометрическое определение
Представьте себе ящик. Давайте назовем его «Кубик». У этого ящика будет дно, верхняя крышка и четыре стенки со всех сторон. Если мы посмотрим сверху на «Кубик», мы увидим квадратное основание. Оно служит базой для всей структуры, дает ей устойчивость и определяет ее форму.
Основание куба является его самой важной частью. Оно определяет не только его форму, но и его свойства. Квадратное основание является источником силы для всех остальных сторон куба. Основание обеспечивает кубу жизненную поддержку и дает ему базу, на которой он может стоять прямо и устоять перед любыми внешними воздействиями.
Итак, геометрическое определение основания куба — это квадратная плоскость, которая служит базой для всей структуры куба. Оно определяет его форму, дает ему устойчивость и является источником силы для остальных его сторон.
Алгебраическое определение
Алгебраическое определение позволяет нам увидеть связь между основанием и кубическим значением. Если мы знаем значение куба, то можем найти его основание, и наоборот.
Например, если дано уравнение a^3 = 64, мы можем найти основание куба, возводя в третью степень обе стороны уравнения. В этом случае основание куба равно 4, потому что 4^3 = 64.
Алгебраическое определение также помогает нам понять, что основание куба может быть как положительным, так и отрицательным числом. Например, a^3 = -27. В этом случае основание куба равно -3, так как (-3)^3 = -27.
Также помните, что основание куба может быть рациональным или иррациональным числом. Например, a^3 = 8. В этом случае основание куба равно 2, так как 2^3 = 8. Однако существуют иррациональные основания куба, например, a^3 = 27. В этом случае основание куба равно кубическому корню из 27, что равно примерно 3, как и предыдущий пример.
Итак, алгебраическое определение позволяет нам легко находить значение основания куба, если дано его кубическое значение, а также понимать различные типы основания — положительные, отрицательные, рациональные и иррациональные числа.
Свойства куба
1. Все стороны куба равны между собой. Это означает, что каждая сторона куба имеет одинаковую длину. Благодаря этому свойству куб имеет симметричную форму и кажется идеально сбалансированным.
2. Все углы куба прямые. Угол — это точка пересечения двух сторон. В случае куба все углы равны 90 градусам, что делает его особенно удобным для строительства и дизайна.
3. Все ребра куба параллельны и перпендикулярны граням. Ребро — это отрезок, который соединяет две вершины куба. Все ребра куба параллельны друг другу и перпендикулярны граням, что делает его геометрически стабильным и прочным.
4. Объем куба вычисляется по формуле V = a^3, где а — длина стороны куба. Вычисление объема куба — это очень полезное свойство, особенно при работе с геометрическими задачами и инженерными расчетами.
5. Площадь поверхности куба вычисляется по формуле S = 6a^2, где а — длина стороны куба. Площадь поверхности куба — это сумма площадей всех его граней. Это свойство позволяет определить, сколько материала потребуется для покрытия поверхности куба, например, в строительстве.
Все эти свойства делают куб интересным и важным геометрическим телом. Он часто используется в архитектуре, дизайне и инженерии.
Стороны и углы куба
Возьмем куб и посмотрим на него внимательно. У него есть шесть сторон: лицевая, задняя, верхняя, нижняя, левая и правая. Все они равны и представляют собой квадраты. Куб также имеет восемь углов, все они прямые.
Когда мы говорим о сторонах куба, мы можем обратиться к ним как к «граням». Грани куба — это его стороны. И все они имеют одинаковую форму — квадратную. Каждый угол, где встречаются две грани, называется вершиной. Куб имеет восемь вершин.
Теперь давайте представим, что ваши друзья хотят построить куб из геометрических блоков. Они выбрали задачу и готовы приступить к работе. Вам нужно объяснить им, что стороны и углы куба являются одинаковыми и прямыми. Это позволит им точно измерить и сконструировать каждую часть куба.
Представьте, что вы стоите рядом с кубом и рассматриваете его. Вы видите, что каждая сторона имеет одинаковую длину и все углы прямые. Здесь нет никаких кривых линий или остроугольных углов. Все части куба прямые и ровные. Это делает куб стабильным и устойчивым.
Так как стороны и углы куба одинаковые, вы можете использовать их, чтобы найти его объем и площадь. Объем куба — это количество пространства, занимаемого им, и он равен длине одной стороны, возведенной в куб. Площадь одной стороны куба вычисляется путем возведения ее длины в квадрат.
Вот какие удивительные свойства имеют стороны и углы куба. Они делают куб уникальным геометрическим телом, подводящим нас к пониманию форм и пространства. Их равномерность и прямые углы делают куб одним из самых простых тел для изучения и понимания в математике и геометрии.
Диагонали куба

Первое, что хотелось бы отметить, это то, что диагонали куба равны между собой. Давайте представим, что у нас есть куб, и мы проводим диагонали от одной вершины к другой. Обратите внимание, что эти две диагонали имеют одинаковую длину. Это означает, что если одна диагональ равна d, то и вторая диагональ также будет равна d.
Одно из интересных свойств диагоналей куба связано с их взаимосвязью с сторонами куба. Диагональ куба будет равна противоположной стороне куба, умноженной на корень квадратный из двух. Другими словами, если сторона куба равна a, то диагональ будет равна a√2. Это можно записать математическим выражением: d = a√2.
А что происходит с площадями граней куба? Когда мы взглянем на диагонали, мы увидим, что они делят грани куба на две равные части. Таким образом, площадь каждой грани будет равна половине площади соответствующей грани. Это означает, что площадь каждой грани куба равна половине площади одной диагонали, умноженной на корень квадратный из двух: S = (1/2) * a^2 * √2.
И наконец, что происходит с объемом куба? Объем куба можно вычислить, зная длину его стороны. Он равен стороне, возведенной в куб: V = a^3. Но мы также можем выразить объем куба через диагональ и площадь грани. Обратите внимание, что объем куба равен произведению длины любой из его диагоналей на площадь грани, деленное на корень квадратный из двух. Это дает нам формулу: V = (a * S) / √2.
Вы обратили внимание на то, как все эти свойства диагоналей куба связаны друг с другом? Уже заинтересовался? Тогда давайте продолжим изучать математические аспекты куба и его диагоналей.
- Диагонали куба равны между собой. Это значит, что диагональ, соединяющая противоположные вершины куба, имеет такую же длину, как и другая диагональ.
- Диагональ куба равна противоположной стороне, умноженной на корень квадратный из двух. Если сторона куба равна a, то диагональ будет равна a√2.
- Площадь каждой грани куба равна половине площади соответствующей диагонали. Это означает, что площадь каждой грани куба равна половине площади одной диагонали, умноженной на корень квадратный из двух: S = (1/2) * a^2 * √2.
- Объем куба можно выразить через длину стороны, диагональ и площадь грани. Объем куба равен произведению длины диагонали на площадь грани, деленное на корень квадратный из двух: V = (a * S) / √2.
Я надеюсь, что эти интересные свойства диагоналей куба заинтриговали вас и вдохновили изучать больше о геометрии! Вопрос для вас: какая из этих формул вас больше всего удивила? Расскажите нам в комментариях ниже!
Основание куба: определение и свойства
Основание куба является плоской фигурой, образованной четырьмя одинаковыми отрезками. В кубе все основания параллельны друг другу и перпендикулярны боковым граням.
Свойства основания куба:
- Все стороны основания куба равны между собой.
- Углы между сторонами основания прямые.
- Все основания куба параллельны друг другу.
- Основания куба перпендикулярны боковым граням.
Основание куба играет важную роль в определении других характеристик куба, таких как объем и площадь поверхности. Площадь основания куба вычисляется как квадрат длины стороны основания, а объем куба вычисляется как куб длины стороны основания.