Когда мы говорим о треугольниках, одна из важных характеристик, на которую мы обращаем внимание, это основание. Основание треугольника — это одна из его сторон, на которую опирается треугольник. Оно играет важную роль в определении типа треугольника и позволяет нам проводить различные геометрические операции.
Основание треугольника имеет несколько свойств. Во-первых, оно является наибольшей стороной треугольника в случае прямоугольного треугольника. Во-вторых, оно определяет высоту треугольника — линию, проведенную из вершины треугольника к основанию, перпендикулярно основанию. Также, основание является базой для вычисления площади треугольника по формуле “половина площади основания на высоту”.
Давайте рассмотрим несколько примеров для более ясного представления о базах треугольников. Например, треугольник со сторонами 5, 7 и 10. Здесь сторона 10 будет основанием треугольника. У другого треугольника со сторонами 3, 4 и 5 основание будет равно 4.
Определение треугольника
Главное свойство треугольника заключается в том, что сумма длин любых двух его сторон всегда больше, чем длина третьей стороны. Это неравенство называется неравенством треугольника и является основным свойством, отличающим треугольник от других фигур. Благодаря этому свойству треугольник может быть натянут на раму или повернут в разных равноконтурных фигурах.
Треугольник можно классифицировать по различным критериям, включая углы и стороны. Углы могут быть острыми (меньше 90 градусов), тупыми (больше 90 градусов) или прямыми (равны 90 градусам). Стороны могут быть равными или неравными, а углы могут быть равными или разными. Существует шесть особых типов треугольников, которые имеют определенные свойства и характеристики.
- Равносторонний треугольник: все стороны равны друг другу.
- Равнобедренный треугольник: две стороны равны друг другу.
- Прямоугольный треугольник: один угол равен 90 градусов.
- Остроугольный треугольник: все углы острые (меньше 90 градусов).
- Тупоугольный треугольник: один угол тупой (больше 90 градусов).
- Разносторонний треугольник: все стороны и углы разные.
Знание основных свойств и типов треугольников является необходимым для решения геометрических задач и проведения различных измерений на плоскости. Понимание треугольников помогает нам лучше понять и воздействовать на окружающий мир, точно описывать формы и находить решения для разнообразных практических задач.
Стороны треугольника
Каждая сторона треугольника представляет собой отрезок, соединяющий две вершины треугольника. А вот что интересно, стороны треугольника могут быть разной длины! Одна сторона может быть короткой, а другая — длинной. Эта разнообразие дает треугольнику его особый вид и уникальные свойства.
По длине стороны треугольников разделяются на три типа:
- Равносторонний треугольник: все три стороны равны друг другу.
- Равнобедренный треугольник: две стороны равны, а третья сторона отличается.
- Разносторонний треугольник: все три стороны имеют разную длину.
Теперь давай поговорим о важном вопросе: зачем нам вообще нужны стороны треугольника? Ответ прост: они помогают нам решать геометрические задачи! Стороны треугольника вместе с его углами образуют основу для вычислений, определения периметра и площади треугольника, а также для нахождения других интересных закономерностей.
Запомни, что стороны треугольника играют важную роль в геометрии и помогают нам лучше понять мир вокруг нас. И не забывай обращать внимание на их длину и отношения между ними! Теперь ты готов исследовать разнообразные треугольники и находить удивительные свойства, скрытые в их сторонах.
Углы треугольника
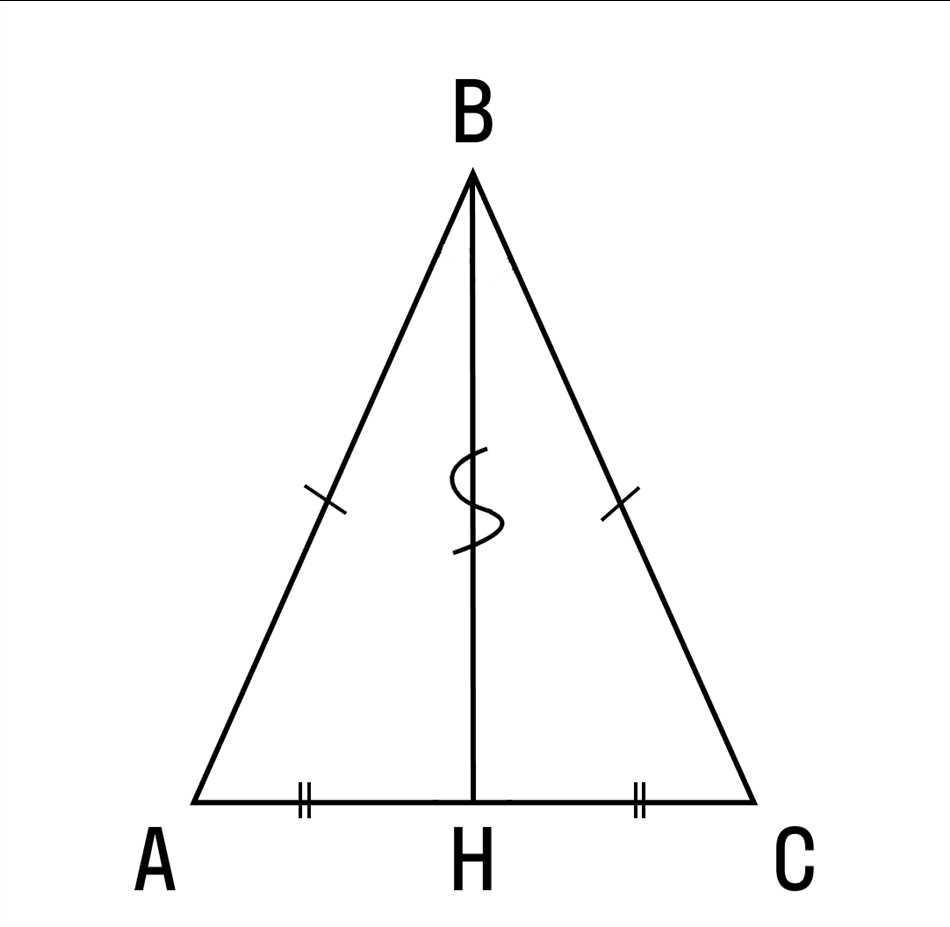
Определение углов треугольника
В треугольнике углы определяются тремя вершинами этой фигуры. Каждая вершина треугольника соединена двумя сторонами, и угол образуется между этими сторонами. Треугольник имеет три угла, поэтому он называется трехугольником.
Сумма углов треугольника
Одно из важнейших свойств углов треугольника – это то, что сумма всех трех углов равна 180 градусам. Это правило называется «сумма углов треугольника». Независимо от вида и размеров треугольника, сумма его углов всегда будет равна 180 градусам. Это очень полезное знание, которое может помочь нам в решении различных задач, связанных с треугольниками.
Виды углов треугольника
Углы треугольника могут быть различных видов в зависимости от их величины. Различают следующие виды углов треугольника:
- Острый угол: угол, меньший 90 градусов;
- Прямой угол: угол, равный 90 градусам;
- Тупой угол: угол, больший 90 градусов, но меньше 180 градусов.
Заключение
Углы треугольника — это важный аспект геометрии, который помогает нам анализировать и понимать свойства треугольников. Зная определение углов треугольника и их сумму, мы можем рассчитывать на успешное решение задач, связанных с треугольниками. Будьте внимательны и упражняйтесь в решении геометрических задач, чтобы стать настоящими экспертами в геометрии!
Основание треугольника
Основание треугольника играет важную роль в его свойствах и определениях. Например, мы можем разделить треугольник на две равные части по прямой, проходящей через середину основания. Эта прямая называется медианой треугольника и всегда проходит через середину основания. Кроме того, перпендикуляр, опущенный на основание треугольника из его вершины, является высотой треугольника. Высота всегда перпендикулярна к основанию и проходит через его середину.
Основание треугольника также используется для определения его типа. Если все три стороны треугольника равны, то его основание будет являться его единственной стороной, а треугольник будет равносторонним. В этом случае, основание и высота треугольника будут совпадать.
Кроме равносторонних треугольников, есть также равнобедренные треугольники. В равнобедренном треугольнике две стороны равны между собой, а основание и высота также равны. Однако, основание равнобедренного треугольника не является его единственной стороной, поскольку третья сторона отличается от них.
Основание треугольника может быть и прямоугольным. В прямоугольном треугольнике, один из его углов равен 90 градусам. В этом случае, основание является гипотенузой треугольника, а его стороны перпендикулярны к основанию.
Как видно из всех этих примеров, основание треугольника является одним из главных составляющих его свойств и характеристик. Оно определяет медианы, высоты, типы и другие аспекты треугольника. Поэтому важно хорошо понять и знать основание треугольника, чтобы лучше разбираться в его геометрических свойствах и использовать их в различных задачах и ситуациях.
Свойства оставшихся сторон и углов
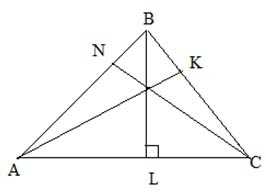
Первое свойство, о котором я хотел бы сказать, – это то, что сумма длин двух любых сторон треугольника всегда больше, чем длина третьей стороны. Это свойство называется неравенством треугольника. Но почему это так? Давайте вместе разберемся.
Представьте, что у нас есть треугольник со сторонами a, b и c. Согласно неравенству треугольника, сумма длин сторон a и b всегда больше длины стороны c. Это можно понять так: если бы сумма длин сторон a и b была равна длине стороны c, то все три стороны были бы вытянуты на одну прямую и треугольник получился бы вырожденным – ведь у него не было бы площади. Поэтому неравенство треугольника всегда выполняется.
Кроме того, есть еще одно важное свойство треугольника – сумма углов треугольника всегда равна 180 градусам. Но почему так происходит? Чтобы это понять, давайте рассмотрим треугольник более внимательно.
В треугольнике у нас есть три угла – A, B и C. Если мы продолжим стороны A и C, они встретятся в точке D, и получится новый угол E. Аналогично, если мы продолжим стороны B и C, они встретятся в точке F, и получится угол G. Таким образом, у нас получится четырехугольник ACFG.
Заметим, что в этом четырехугольнике уголы A, B, C, E, F и G образуют окружность, поэтому их сумма равна 360 градусов. Но у нас есть две пары вертикально противоположных углов AFG и CEF, которые равны друг другу. Исходя из этого, сумма углов треугольника ABC равна половине суммы углов окружности, то есть 180 градусам.
И наконец, не забудьте, что в треугольнике может быть один прямой угол, два острых угла или два тупых угла. Все эти комбинации возможны, если сумма углов треугольника равна 180 градусам, и каждый угол находится в определенном диапазоне значений. Например, если один угол треугольника равен 90 градусам, то два оставшихся угла должны быть острыми, и их сумма будет меньше 90 градусов.
Так что следующий раз, когда вы будете работать с треугольниками, не забудьте об этих свойствах. Они помогут вам лучше понять и использовать геометрию треугольников в различных задачах. Удачи!
Основание треугольника: определение, свойства и примеры
Некоторые свойства основания треугольника:
- Основание треугольника является одной из его сторон.
- Длина основания может быть различной для разных треугольников.
- Основание треугольника может быть горизонтальной или вертикальной стороной.
- Если треугольник равнобедренный, то его основание будет стороной, не являющейся равными боковыми сторонами.
- В прямоугольном треугольнике основание является наибольшей стороной и противоположно прямому углу.
Примеры треугольников с указанием их оснований:
- Равнобедренный треугольник ABC, где AB = AC. Основание — сторона BC.
- Разносторонний треугольник XYZ. Основание — сторона YZ.
- Прямоугольный треугольник PQR с прямым углом в точке Q. Основание — сторона PQ.
Понимание основания треугольника и его свойств помогает в решении геометрических задач и вычислении параметров треугольника.