Основные понятия и свойства окружности

Уверен, что ты уже хоть раз в жизни слышал о «окружности». Окружность – это не просто фигура в геометрии, это также ключевой элемент, который находит применение во многих областях науки и техники.

Это захватывающее понятие имеет свои особенности и интересные свойства. Давай же разберемся в его определении, а также рассмотрим основные понятия, связанные с окружностью, чтобы ты мог легко разобраться в этой теме и применить ее в своей жизни и работе.

Что такое окружность?

Одной из первых вещей, которую мы узнаем о окружности, это ее радиус. Радиус — это расстояние от центра окружности до любой точки на ней. Когда мы говорим о радиусе, мы часто используем букву «r» для его обозначения.

Как и любая другая фигура, окружность имеет свои уникальные свойства. Например, длина окружности может быть рассчитана с использованием формулы πD, где D — это диаметр окружности (диаметр — это двукратное расстояние от одной точки на окружности до противоположной точки). Другое важное свойство окружности — ее площадь, которая может быть рассчитана с использованием формулы πr², где r — радиус окружности. И пусть никто вам не говорит, что формулы скучны и ненужные. Знание этих формул поможет вам решить множество геометрических задач и применить их в реальной жизни, ведь окружности не только красивы сами по себе, они также имеют практическое значение.

Но окружность — это не только числа и формулы. Она также имеет символическое значение и используется в различных культурах и религиях. Многие видят в окружности символ бесконечности, совершенства и вечности. Окружность также может представлять гармонию и единство, так как все точки на ней находятся на одинаковом расстоянии от центра.

Так что, давайте восхитимся и изучим окружность и ее свойства. Она не только поможет нам лучше понять мир вокруг нас, но и может стать источником вдохновения и красоты в нашей жизни.

Главные элементы окружности

Центр окружности

Один из главных элементов окружности — это ее центр. Это точка, от которой все остальные точки на окружности находятся на одинаковом расстоянии. Центр окружности обычно обозначается буквой O и может быть любой точкой на плоскости.

Радиус окружности

Радиус окружности — это расстояние от центра окружности до любой точки на ней. Обозначается буквой r. Радиус — это ключевой элемент окружности, так как он определяет ее размер. Он может быть разной длины в разных окружностях.

Диаметр окружности

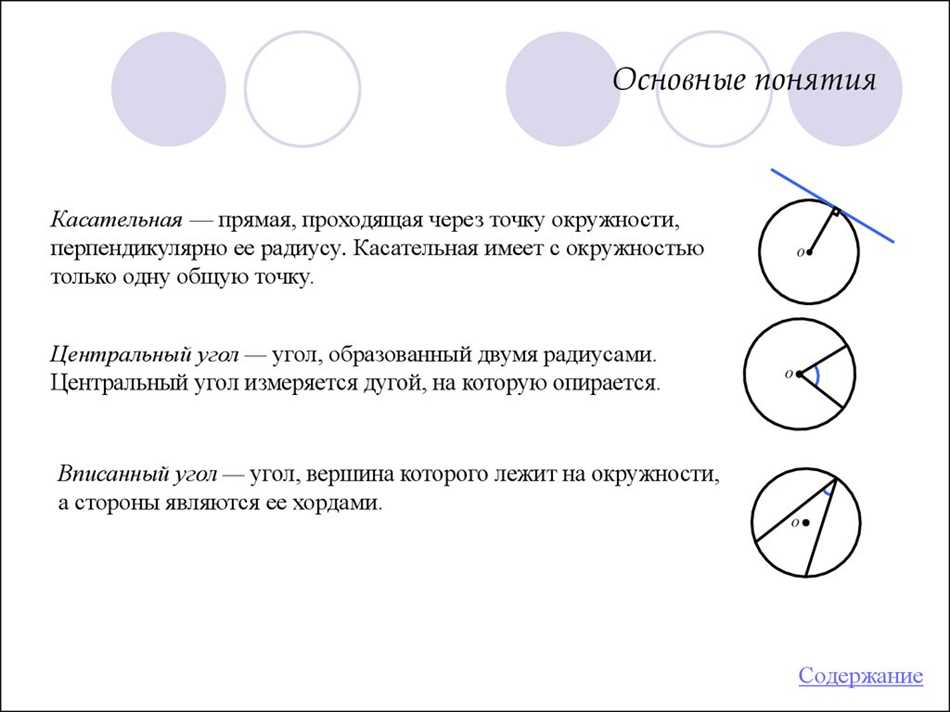
Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр обозначается буквой d и является удвоением радиуса (d = 2r). Диаметр — это еще один важный элемент окружности, который также определяет ее размер.

Хорда окружности

Хорда — это отрезок, соединяющий две точки на окружности. Хорда может быть любой длины и может быть как диаметром окружности, так и меньше диаметра. Хорда — это важный элемент окружности, который играет важную роль в ее свойствах.

Дуга окружности

Дуга — это часть окружности, которая между двумя точками на ее окружности. Дуга — это еще один интересный элемент окружности, который можно изучать и измерять. Дуга может быть дугой диаметра, дугой хорды или любой другой дугой, в зависимости от ее положения и размера.

Эти главные элементы окружности — центр, радиус, диаметр, хорда и дуга — помогают нам разобраться в ее основных свойствах и использовать их в математике, геометрии и других областях нашей жизни. Зная эти элементы, мы можем строить и анализировать окружности, решать задачи и находить интересные связи между ними. Теперь давайте зададим себе вопрос: «Каким образом мы можем использовать знания об окружности в нашем повседневной жизни?»

Основные формулы и свойства окружности

Окружность и ее радиус

Радиус — это отрезок, соединяющий центр окружности с любой из ее точек. Он является основным элементом окружности и обозначается символом «r». Радиус определяет размер окружности и является половиной диаметра.

Длина окружности (L) может быть вычислена с использованием формулы:

L = 2πr

где «π» — это математическая константа, примерно равная 3.14159. Для лучшей точности, значение «π» можно округлить до большего количества десятичных знаков.

Окружность и ее диаметр

Диаметр — это отрезок, проходящий через центр окружности и соединяющий две противоположные точки на ее границе. Диаметр обозначается символом «d» и является двукратным радиуса.

Формула для вычисления длины окружности также может быть записана через диаметр:

L = πd

Площадь окружности

Площадь окружности (S) может быть вычислена по формуле:

S = πr²

где «r» — это радиус окружности. Площадь окружности является мерой ее поверхности и выражает, какая площадь может быть занимаема окружностью.

Углы на окружности и дуги

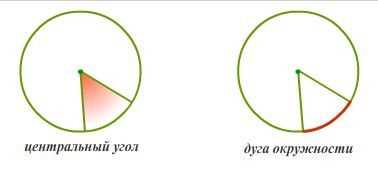
Если мы проведем отрезок, соединяющий две точки на окружности, называемые концевыми точками, то это создает дугу окружности. Угол между двумя радиусами, проведенными к концевым точкам дуги, называется центральным углом.

Если мы проведем отрезок, соединяющий центр окружности с точкой на дуге, это будет называться радиусом дуги. Радиус дуги также является радиусом окружности.

Теорема о центральном угле

Теорема о центральном угле утверждает, что центральный угол, образованный на окружности, равен углу, образованному любым радиусом, проведенным к концевым точкам дуги.

Это свойство позволяет нам вычислять неизвестные углы на окружности и использовать их в решении геометрических задач.

Теорема касательных

Теорема касательных утверждает, что линия, касающаяся окружности в единственной точке, перпендикулярна радиусу, проведенному в этой точке. Это свойство касательной позволяет нам решать задачи, связанные с построением касательной к окружности в заданной точке.

Дуги и длина дуги

Дуга — это часть окружности между двумя ее точками. Длина дуги (l) может быть вычислена с использованием формулы:

l = rθ

где «r» — это радиус окружности, а «θ» — это центральный угол, измеряемый в радианах.

Зная длину дуги, мы можем определить периметр (P) сектора окружности с помощью формулы:

P = l + 2r

Основные формулы и свойства окружности — это важные инструменты, которые помогают нам исследовать, решать задачи и понимать геометрические отношения вокруг нас. При решении задач с окружностями, нам необходимо использовать эти формулы и свойства, чтобы получить правильные ответы и лучше понять окружающий нас мир.

Примеры задач, связанных с окружностью

Ниже приведены несколько примеров задач, которые можно решить, используя свойства окружности:

1. Задача о нахождении длины окружности:

   Пусть дана окружность с радиусом r. Чтобы найти длину окружности, можно использовать формулу:

   Длина окружности = 2πr

   Например, если радиус окружности равен 5 см, то длина окружности будет равна 10π см (или примерно 31,42 см).

2. Задача о нахождении площади круга:

   Площадь круга можно найти, зная радиус r. Формула для вычисления площади круга:

   Площадь круга = πr²

   Например, если радиус круга равен 3 м, то площадь круга будет равна 9π м² (или примерно 28,27 м²).

3. Задача о построении касательной:

   Дана окружность с центром O и радиусом r. Чтобы построить касательную к окружности в заданной точке P на окружности, можно использовать следующий алгоритм:

   • 1. Провести прямую, проходящую через центр окружности O и точку P. Эта прямая будет перпендикулярна касательной.
   • 2. Создать небольшую дугу на окружности, используя точку P и радиус r.
   • 3. Найти середину этой дуги и обозначить ее как точку A.
   • 4. Провести прямую, проходящую через точки O и A. Эта прямая будет касательной к окружности в точке P.

4. Задача о построении окружности через три заданные точки:

   Даны три точки A, B и C. Чтобы построить окружность, проходящую через эти три точки, можно использовать следующий алгоритм:

   • 1. Найти середины отрезков AB и BC и обозначить их как точки M и N соответственно.
   • 2. Провести перпендикуляры к отрезкам AB и BC из точек M и N соответственно.
   • 3. На пересечении этих перпендикуляров будет находиться центр окружности.
   • 4. Используя полученный центр и любую из трех исходных точек, построить окружность.

5. Задача о вычислении радиуса окружности, определенной тремя заданными точками:

   Даны три точки A, B и C на окружности с центром O. Чтобы найти радиус окружности, можно использовать следующий алгоритм:

   • 1. Найти середины отрезков AB, AC и BC и обозначить их как точки M, N и P соответственно.
   • 2. Вычислить длины отрезков AM, AN и AP.
   • 3. Найти полупериметр треугольника, образованного точками A, B и C, используя формулу:
     Полупериметр = (AB + AC + BC) / 2
   • 4. Вычислить радиус окружности, используя формулу для радиуса описанной окружности треугольника:
     Радиус = sqrt((Полупериметр — AB) * (Полупериметр — AC) * (Полупериметр — BC) / Полупериметр)

Приведенные примеры задач показывают только небольшую часть возможностей использования окружности в решении различных задач. Окружность – универсальная фигура, обладающая множеством свойств и применений. Изучение основных понятий окружности и решение задач, связанных с ней, помогает развивать абстрактное мышление, логику и пространственное воображение.

Окружность и ее свойства: основные понятия

Окружность имеет несколько важных свойств:

• Радиус — это расстояние от центра окружности до любой точки на окружности. Обозначается символом r.
• Диаметр — это отрезок, который соединяет две точки на окружности и проходит через ее центр. Диаметр равен удвоенному значению радиуса: d = 2r.
• Окружность делится на две части, называемые сектором и дугой. Сектор — это фигура, ограниченная двумя радиусами и дугой окружности, а дуга — это часть окружности между двумя точками.
• Длина окружности — это периметр окружности, то есть сумма длин всех дуг окружности. Длина окружности зависит только от ее радиуса и вычисляется по формуле: l = 2πr, где π (пи) — математическая константа, примерное значение которой равно 3.14159.

Также существуют другие важные понятия, связанные с окружностью, такие как хорда, касательная, секущая и радиус-вектор, но они выходят за рамки данного краткого описания основных понятий.