Особенности современной математики: открытия, тенденции, приложения

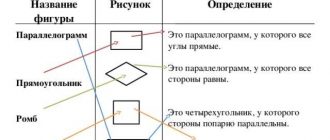
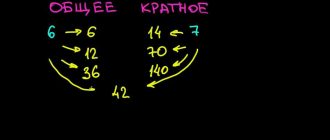
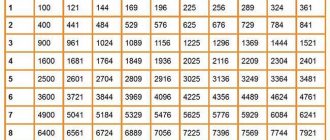
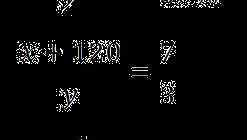Современная математика – это раздел науки, который занимается изучением формальной логики, чисел, структур, пространств и математических моделей. В отличие от классической математики, современная математика активно использует компьютерные технологии. В современной математике появились новые разделы, такие как теория вероятности, теория графов, математическая статистика и дискретная математика. Современные математические методы и инструменты широко применяются в различных областях, включая физику, экономику, биологию и компьютерные науки.

Развитие новых методов решения задач

Одним из основных факторов, способствующих развитию новых методов, является компьютерное моделирование. С помощью компьютерных программ и алгоритмов математики могут решить задачи, которые ранее считались неразрешимыми. Например, в современной криптографии, где задачей является нахождение простых чисел больших размеров, математики используют вычислительные методы для поиска новых чисел и проверки их простоты. Благодаря этому, сейчас мы имеем более надежные системы шифрования и защиты данных.

Еще одним важным аспектом развития новых методов является использование методов и инструментов других научных дисциплин. Например, математики часто используют методы статистики и вероятности для решения задач, связанных с прогнозированием и анализом данных. Также они активно используют техники оптимизации, которые разрабатываются в области исследования операций и линейного программирования. Это позволяет им решать задачи более эффективно и находить оптимальные решения.

Важно отметить, что развитие новых методов решения задач невозможно без сотрудничества и обмена идеями между математиками со всего мира. Международные конференции, научные журналы и форумы играют важную роль в обмене знаниями и опытом. Именно благодаря такому сотрудничеству, новые методы решения задач разрабатываются и совершенствуются.

В окончании, современная математика развивается и открывает новые горизонты в решении задач. Благодаря компьютерному моделированию, использованию методов других научных дисциплин и сотрудничеству между математиками, мы получаем новые инструменты, которые помогают нам решать сложные проблемы и находить оптимальные решения.

Использование вычислительной техники в математике

Современная математика неразрывно связана с использованием вычислительной техники. Компьютеры и программы позволяют математикам ускорять и упрощать решение сложных математических задач, а также проводить большие и долгие вычисления за короткое время.

Одним из главных преимуществ использования вычислительной техники в математике является возможность работы с большими объемами данных. Математические модели и задачи становятся все более сложными, и обработка такого количества информации уже невозможна без помощи компьютеров. Вычислительные мощности современных компьютеров позволяют математикам решать задачи, которые раньше занимали бы невообразимое количество времени.

Один из ярких примеров использования вычислительной техники в математике — это компьютерные эксперименты. Математики могут создавать модели и симуляции, чтобы исследовать поведение сложных систем или проверить гипотезы. Например, при исследовании динамики популяции могут быть созданы модели, которые учитывают множество факторов, таких как рождаемость, смертность, миграция и взаимодействие среди особей. С помощью компьютерных симуляций можно оценить влияние каждого фактора на популяцию и предсказать ее будущее состояние.

Вычислительная техника также является неотъемлемой частью математических исследований. Математики используют программы для символьных и численных вычислений, графической визуализации результатов и создания математических моделей. Программы, такие как MATLAB и Mathematica, обладают мощными возможностями и являются незаменимым инструментом для исследования и решения математических задач.

Однако, несмотря на все преимущества использования вычислительной техники в математике, она не является панацеей для всех проблем. Важно помнить, что программы и компьютеры выполняют только то, что им было сказано, и не всегда учитывают все возможные варианты. Поэтому важно быть критическим и внимательным при использовании вычислительной техники, чтобы получить надежные и точные результаты.

Роль компьютерных программ в современной математике

Современная математика переживает настоящую революцию благодаря развитию компьютерных технологий. Компьютерные программы играют важную роль в работе математиков, помогая им решать сложные задачи и делать новые открытия. В этом тексте я расскажу о том, как компьютерные программы изменяют мир математики и почему они стали неотъемлемой частью ее развития.

1. Вычисления и численное моделирование

Одно из главных преимуществ компьютерных программ в математике заключается в их способности выполнять сложные вычисления и проводить численное моделирование. Когда математические задачи становятся настолько сложными, что решить их аналитически невозможно или экономически нецелесообразно, компьютерные программы приходят на помощь. Они позволяют математикам находить численные значения функций, решать интегралы и дифференциальные уравнения, а также проводить сложные математические моделирования.

Используя компьютерные программы, математики могут анализировать большие объемы данных, делать предсказания и оценивать вероятности, что помогает им принимать более обоснованные решения в различных областях, включая физику, экономику, биологию и информатику. Компьютерные программы стали незаменимым инструментом для решения практических задач и улучшения нашего понимания мира.

2. Визуализация и взаимодействие

Компьютерные программы также сильно помогают математикам визуализировать сложные математические объекты и представлять их в понятной форме. Благодаря программам для визуализации, математики могут увидеть трехмерные графики, динамику функций, сложные геометрические формы и многое другое. Это помогает им лучше понять структуру задачи и найти новые способы ее решения.

Кроме того, компьютерные программы предоставляют математикам возможность взаимодействия с математическими объектами. Например, с помощью интерактивных программ, математики могут изменять параметры функций и наблюдать, как меняется их поведение. Это позволяет им экспериментировать, строить гипотезы и проверять их на практике.

3. Коллаборация и обмен результатами

Интернет и компьютерные программы также дали возможность математикам со всего мира сотрудничать, обмениваться результатами и проводить совместные исследования. Благодаря платформам для совместной работы над математическими задачами, математики могут обмениваться идеями, комментировать результаты и работать над проектами вместе, несмотря на то, что они находятся в разных странах и даже на разных континентах.

Этот новый уровень коллаборации и обмена информацией способствует быстрым и значимым открытиям, помогает математикам из разных областей объединять свои силы и решать комплексные задачи. Также это дает возможность молодым математикам внести свой вклад и получить обратную связь и поддержку от опытных специалистов.

Компьютерные программы действительно изменили мир математики, открыв новые горизонты и ускорив развитие этой науки. Они помогают математикам решать сложные задачи, визуализировать результаты и обмениваться информацией. Если вы интересуетесь математикой, лучше всего начать знакомство с этой наукой с освоения программирования и работы с компьютерными программами. С ними мир математики становится доступным и захватывающим для всех!

Математические модели и их применение

Математическая модель представляет собой упрощенное описание реального мира, основанное на математических законах и принципах. Она позволяет с помощью математических выражений и уравнений описывать и предсказывать поведение объектов и систем. Математические модели используются во многих областях, таких как физика, экономика, биология, компьютерные науки и т.д. Они помогают ученым и исследователям лучше понять сложные явления и процессы, а также принимать важные решения.

Использование математических моделей имеет множество преимуществ. Во-первых, они позволяют проводить виртуальные эксперименты, что снижает риски и затраты на реальные исследования. Также математические модели позволяют предсказывать и анализировать различные сценарии развития событий, что помогает принимать эффективные решения и планировать будущее.

Применение математических моделей находит свое применение во многих областях жизни. Например, в экономике они применяются для моделирования рынков, предсказания тенденций и принятия инвестиционных решений. В медицине математические модели используются для прогнозирования распространения заболеваний и разработки эффективных стратегий лечения.

Кроме того, математические модели важны в сфере технологий. Например, в автомобильной промышленности они используются для моделирования процессов, связанных с разработкой и тестированием новых моделей автомобилей. В аэрокосмической отрасли математические модели позволяют прогнозировать и анализировать поведение космических аппаратов и спутников.

В заключении можно сказать, что математические модели играют важную роль в современном мире. Они помогают нам лучше понимать и контролировать различные процессы, а также принимать правильные решения. Поэтому развитие математической науки и применение ее моделей является ключевым фактором для прогресса и развития общества.

Интердисциплинарный характер математики

Интердисциплинарность математики становится особенно явной в современном научном и технологическом прогрессе. Применение математических методов и моделей в различных областях знаний позволяет ученым получать новые уникальные результаты и решать сложные задачи.

Например, в биологии математические модели могут быть использованы для изучения протекания биохимических реакций или взаимодействия генов. Математика помогает понять сложные процессы, которые трудно изучать экспериментально.

В экономике математическое моделирование используется для анализа рынков, прогнозирования цен и принятия решений в условиях неопределенности. Математика становится неотъемлемой частью финансового мира и биржевой торговли.

Но не только прикладные науки нуждаются в математике. Сама математика постоянно развивается благодаря комбинированию и взаимодействию различных интеллектуальных дисциплин. Интердисциплинарный подход позволяет создавать новые математические теории и методы, которые впоследствии могут быть применены в других областях.

Так, компьютерные науки и информатика тесно связаны с математикой. Математические алгоритмы стали основой для разработки программного обеспечения и искусственного интеллекта. Интердисциплинарность позволяет совмещать знания и методы разных наук для достижения новых высот.

В конечном итоге, интердисциплинарный характер математики открывает перед нами огромные возможности для решения самых сложных проблем. Он позволяет ученым взглянуть на проблему с разных сторон и применить разнообразные инструменты и подходы. Математика становится единственным языком и связующим звеном между различными науками.

Развитие математической логики

Представьте, что вы находитесь в игре экономического симулятора, где вам предстоит принимать сложные решения, основанные на математических расчетах. Может быть, это принятие решений о том, как распределить ресурсы между производственными отделами, или о том, когда лучше продать акции на фондовом рынке. Все это требует от вас точной логики и способности анализировать сложные проблемы. И именно здесь развитие математической логики становится крайне важным.

Одной из ключевых фигур в развитии математической логики был английский математик Джордж Буль. В 19 веке он разработал свою алгебру логики, которая стала основой для современного формализма в логике. Он доказал, что рассуждения можно представить в виде алгебраических выражений, что открыло новые горизонты для математической логики.

С развитием математической логики появились различные системы символов и правил, которые помогают формализовать и структурировать наше мышление. Примером такой системы является математическая нотация, которая позволяет нам записывать и оперировать числами, переменными и операторами. Благодаря этим символам и правилам мы можем строить доказательства и находить решения для сложных математических задач.

Современная математическая логика продолжает развиваться и применяться во многих областях знания. Она играет ключевую роль в искусственном интеллекте, где формальные системы и правила логики используются для создания умных алгоритмов и систем. Кроме того, математическая логика помогает нам анализировать и доказывать свойства математических объектов, таких как группы, поля и топологии.

Таким образом, развитие математической логики и ее применение в различных областях знания демонстрируют, насколько важной она является для нашего современного общества. Без математической логики мы не смогли бы решать сложные проблемы и принимать рациональные решения. Поэтому, развивайте свои навыки математической логики и открывайте новые возможности для себя!

Особенности современной математики

Абстрактность и формализм

Одной из основных особенностей современной математики является ее абстрактность. Математические объекты и концепции моделируются в абстрактных терминах, которые не всегда имеют прямое отражение в реальном мире. Это позволяет математикам решать задачи не только в традиционных областях, но и в новых сферах, таких как криптография или искусственный интеллект.

Еще одним аспектом абстрактности современной математики является формализм. Формализм состоит в том, что математические теоремы и доказательства записываются с помощью формальных символов и правил логики. Такой подход позволяет устанавливать точные и строгие определения, а также проводить доказательства с необходимой ясностью и точностью.

Интердисциплинарность

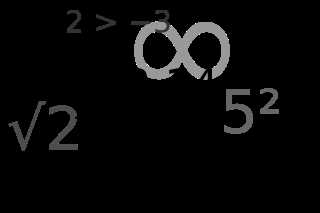
Современная математика является очень интердисциплинарной наукой. Она активно взаимодействует с другими областями знания, такими как физика, компьютерные науки, экономика и т.д. Математические методы и концепции используются для решения сложных проблем в этих областях и дают новые возможности для исследования.

Компьютерное моделирование

Современная математика активно использует компьютерное моделирование для анализа и решения сложных задач. Компьютерные программы позволяют выполнять вычисления, которые раньше были невозможны или чрезвычайно сложны. Благодаря компьютерному моделированию математики могут быстро и наглядно получать результаты и проверять свои гипотезы.

Открытие новых областей и проблем

Современная математика продолжает открывать новые области и проблемы для исследования. В процессе решения одних задач появляются новые вопросы, которые требуют дальнейшего исследования. Иногда новые области математики возникают из-за потребностей и вызовов других наук, а иногда они появляются из чисто теоретических соображений.

Таким образом, современная математика отличается абстрактностью и формализмом, она является интердисциплинарной наукой, активно использует компьютерное моделирование и открывает новые области и проблемы для исследования.