Остаток при делении: определение, примеры и особенности

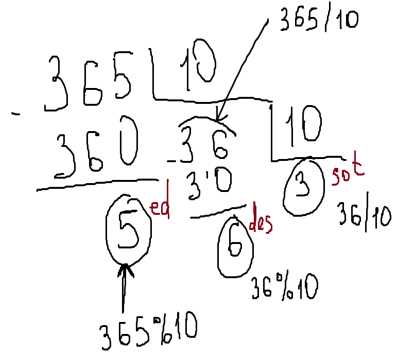
Когда мы делим одно число на другое, возникает понятие «остаток». Но что это значит? Остаток при делении — это число, которое остается после того, как одно число делится на другое без остатка. Иными словами, это «лишние» единицы, которые не могут быть равномерно разделены. Для лучшего понимания, рассмотрим пример: если мы разделим 10 на 3, то останется остаток равный 1. Это значит, что 3 уместится в 10 три раза, а 1 останется «лишним». Остаток при делении играет важную роль в математике и может использоваться для различных вычислений и задач.

Описание остатка при делении

Остаток при делении является важным понятием в математике и используется в различных областях. Например, в программировании остаток при делении используется для определения четности или нечетности числа, а также для вычисления периодичности или повторяемости числовых последовательностей.

Когда мы делаем деление, мы получаем два значения: частное и остаток. Частное — это результат деления, а остаток — это число, которое остается после вычитания числа, полученного из первого значения, из второго значения. Например, если мы разделим число 17 на число 5, частное будет равно 3, а остаток — 2. Это означает, что 17 можно разделить на 5 три раза с остатком 2.

Остаток при делении может быть положительным или отрицательным числом, в зависимости от знаков делимого и делителя. Если делимое отрицательное, а делитель положительное или наоборот, остаток будет отрицательным числом. Например, если мы разделим число -15 на число 4, остаток будет равен -3.

Также стоит обратить внимание на особенность остатка при делении отрицательных чисел. В математике, остаток при делении отрицательных чисел может быть отрицательным или положительным, в зависимости от выбранной системы деления. Например, в системе деления по модулю (обозначается символом %), остатки от деления отрицательных чисел всегда положительны, а в некоторых других системах, остаток может быть и отрицательным числом.

Основные термины и определения

В этом разделе мы рассмотрим основные термины и определения, связанные с остатком при делении. Если вы только начинаете изучать эту тему или нуждаетесь в напоминании, то этот раздел поможет вам разобраться.

Делитель

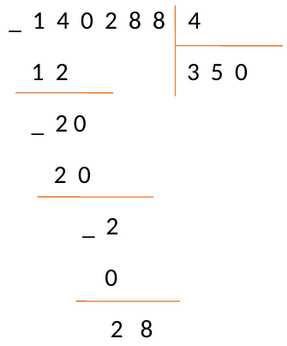
Делитель — это число, на которое делимое делится без остатка. Например, если у нас есть число 10 и мы делим его на 2, делитель будет равен 2.

Делимое

Делимое — это число, которое мы делим на делитель. В нашем предыдущем примере делимое равно 10.

Остаток

Остаток — это число, которое остается после выполнения деления на делитель. Когда мы делим 10 на 2, остаток будет равен 0, потому что 10 делится на 2 без остатка.

Частное

Частное — это результат деления делимого на делитель. В нашем примере, частное будет равно 5, потому что 10 делится на 2 без остатка.

Остаток при делении

Остаток при делении — это остаток, который остается после выполнения деления. Он обозначается символом «%». Например, если мы хотим найти остаток при делении 10 на 3, мы пишем «10 % 3». Ответ будет равен 1, потому что 10 делится на 3 с остатком 1.

Деление нацело

Деление нацело — это деление без остатка. Когда деление не имеет остатка, мы говорим, что оно выполнено нацело. Например, деление 10 на 2 выполнено нацело, потому что оно дает частное 5 и остаток 0.

Неполное деление

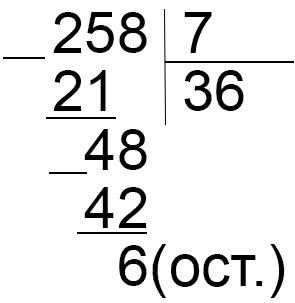
Неполное деление — это деление, которое имеет остаток. Если частное не является целым числом, то это неполное деление. Например, когда мы делим 10 на 3, частное равно 3.3 (примерное значение) и остаток равен 1.

У всех этих терминов есть свои определения и понятия. Понимание и использование этих терминов поможет вам в решении задач и понимании математических концепций.

Как найти остаток при делении?

Остаток при делении можно найти с помощью простых математических операций. Если задача звучит так: «Найдите остаток при делении 15 на 4», то мы можем разделить 15 на 4 и узнать, какое число получится без остатка.

• 4 / 15 = 3 (остаток 3)

В этом примере остаток равен 3. Это значит, что 15 разделить на 4 можно 3 раза без остатка, а оставшийся остаток составляет 3.

Иногда остаток при делении может быть равным 0, что означает, что деление выполняется без остатка. Например, при делении 8 на 2, получаем следующий результат:

• 2 / 8 = 4 (остаток 0)

В этом случае остаток равен 0, так как 8 делится на 2 без остатка.

Можно использовать различные методы для нахождения остатка при делении, включая деление в столбик и использование алгоритма евклида. Какой метод выбрать, зависит от задачи и предпочтений.

Остатки при делении широко используются в математике, арифметике, информатике и других дисциплинах. Они могут быть полезными для решения различных задач, таких как проверка делимости, вычисление площади или нахождение наименьшего общего кратного.

Так что не стесняйтесь использовать остатки при делении в своих математических и арифметических задачах. Они могут помочь вам получить точные и полезные ответы, и даже открыть новые пути для решения сложных задач.

Практические примеры

Погрузимся в мир практических примеров, чтобы лучше понять, как работает остаток при делении. Давайте представим, что у вас есть 10 пирожных, которые нужно разделить поровну между 3 гостями. Как распределить пирожные так, чтобы каждый гость получил одинаковое количество?

Один из путей решить эту задачу — использовать деление с остатком. Вы можете разделить 10 пирожных на 3, и у вас получится 3 целых пирожных для каждого гостя. Но что делать с оставшимся пирожным?

Здесь мы сталкиваемся с понятием остатка при делении. В данном случае, остаток будет равен 1, так как после деления 10 на 3, остается 1 пирожное, которое не может быть равномерно распределено между гостями. Таким образом, вы можете дать каждому гостю по 3 пирожных и оставить последнее пирожное себе.

Теперь представьте, что у вас есть 15 конфет, и вы хотите разделить их между 4 детьми. Как быть в этом случае?

Если вы попробуете решить эту задачу с помощью деления с остатком, то увидите, что каждый ребенок получит по 3 конфеты, а останется 3 конфеты, которые нельзя равномерно распределить между детьми.

В этом случае возникает вопрос: как правильно распределить оставшиеся конфеты? Возможно, вы решите отдать одну конфету каждому из детей и оставить 2 конфеты себе. Или же можно дать все оставшиеся конфеты одному ребенку, чтобы он смог насладиться большим количеством сладостей.

Все эти примеры демонстрируют, что остаток при делении используется для определения того, что остается после равномерного распределения. В жизни у нас часто возникают ситуации, когда нужно разделить что-то на равные части, и остаток при делении помогает нам определить, что делать с оставшимися элементами.

Надеюсь, эти практические примеры помогли вам лучше понять, как работает остаток при делении. Разделение на равные части и определение остатка — важные математические концепции, которые применимы в повседневной жизни.

Арифметика остатка

Представьте себе, что у вас есть большой торт, и вы хотите его поделить между своими друзьями. Но у вас всего 12 друзей, и каждому хочется отведать этот вкусный десерт. Чтобы узнать, сколько кусочков торта достанется каждому другу, нужно применить арифметику остатка.

Основная идея арифметики остатка заключается в том, что при делении одного числа на другое мы можем получить не только частное, но и остаток. В примере с тортом это означает, что мы будем знать, сколько кусочков торта будет полностью поделено между друзьями, а сколько останется без изменений.

Давайте посмотрим на конкретный пример, чтобы лучше понять, как работает эта операция.

Пример:

У вас есть 16 конфет, и вы хотите разделить их между друзьями. Всего у вас 6 друзей. Сколько конфет достанется каждому другу?

Чтобы решить эту задачу, мы просто делим 16 на 6 и получаем частное 2. Это означает, что каждый друг получит 2 конфеты. Но что делать с оставшимися 4 конфетами? Вот тут-то и пригождается арифметика остатка! Мы добавляем знак «%» между числами 16 и 6 и получаем остаток 4. То есть, у каждого друга будет по 2 конфеты, а оставшиеся 4 конфеты останутся у нас.

И это только один из примеров использования арифметики остатка! Она применяется во множестве ситуаций, где необходимо разделить что-то на равные части или решить задачу с остатком.

Теперь вы понимаете, что арифметика остатка – это удивительная и полезная операция, способная помочь вам в решении самых разных задач. Не стоит бояться этой математической операции, ведь она проста и логична! Знание и понимание арифметики остатка поможет вам не только в учебе, но и в повседневной жизни.

Особенности остатка при делении на ноль

В математике существует множество правил и операций, которые помогают нам решать различные задачи. Одна из таких операций – деление. Когда мы делим одно число на другое, мы получаем частное и остаток. Частное – это результат деления, а остаток – это число, которое остается после того, как мы произвели максимальное количество возможных вычитаний.

Однако, когда мы пытаемся поделить что-то на ноль, мы сталкиваемся с проблемой. Представьте себе ситуацию, когда у вас есть 10 яблок, и вы хотите поделить их на ноль корзин. Сколько яблок окажется в каждой корзине? фактически, ничего нельзя разделить на ноль, так как мы не можем распределить объекты на несуществующие группы. Это противоречит логике и смыслу операции деления.

Итак, основная особенность остатка при делении на ноль заключается в том, что он не определен и не имеет значения. В математике это называется «неопределенностью». Все остатки при делении на ноль будут одинаковыми – они не существуют. Поэтому, часто говорится, что деление на ноль – это «деление на ноль не определено» или «деление на ноль запрещено».

Окей, давайте еще раз вместе: невозможно разделить что-то на ноль. Но почему это важно? Представьте себе, какая была бы путаница, если бы было допустимо деление на ноль. Мы бы получили бесконечное количество значений для любого деления и нарушили бы множество математических правил и свойств. Все наше знание и понимание математики были бы неприменимыми.

Так что давайте будем помнить, что деление на ноль не имеет смысла и не определено. Это особенность математики, которую мы должны учитывать. И даже если иногда нам кажется, что остаток при делении на ноль может быть чем-то интересным или полезным, помните, что это противоречит самой сути математических операций и нарушает основные правила и свойства.

Так что, дорогой читатель, давайте будем осторожными при работе с делением и не подпускать деления на ноль. Вместе мы лучше поймем и оценим науку истинного знания – математику. Ведь только понимая и уважая ее правила и особенности, мы сможем достичь большего и преуспеть в этой невероятно интересной и важной области знаний.

Остаток при делении: определение, примеры и особенности

Остаток при делении обозначается знаком «%». Например, остаток от деления числа 7 на 3 равен 1, что записывается как 7 % 3 = 1.

Особенности остатка при делении:

• Остаток при делении всегда меньше делителя и больше или равен нулю.
• Остаток при делении двух положительных чисел всегда положителен.
• Остаток при делении числа на единицу всегда равен нулю.
• Остаток при делении нуля на любое число всегда равен нулю.
• Остаток при делении отрицательного числа на положительное число имеет отрицательное значение.
• Остаток при делении положительного числа на отрицательное число имеет положительное значение.

Примеры использования остатка при делении:

1. Определение четности числа: число без остатка делится на 2, если остаток при делении равен нулю, то число четное, иначе — нечетное.
2. Расчет дней недели: остаток от деления количества дней на 7 позволяет определить, какой день недели будет после заданного количества дней.
3. Хранение информации в массивах: остаток от деления используется для определения индекса элемента в массиве.