В математике отношение играет важную роль и помогает нам лучше понимать взаимосвязь между различными величинами или объектами.
Отношение представляет собой способ сравнения и классификации элементов в множествах. Оно может быть задано с помощью таблицы, диаграммы, формулы или просто словесно. Изучение отношений позволяет нам определить, как один элемент связан с другим и какие свойства имеют эти связи.
Решение математических задач связанных с отношениями требует логического мышления и анализа. В процессе решения мы выявляем особенности отношений, выделяем и классифицируем их свойства и используем эти знания для решения задач и построения моделей.
Давайте изучим отношения в математике более подробно и разберемся, как они помогают нам решать задачи и анализировать мир вокруг нас.
Определение отношения
Так вот, отношение — это связь или соотношение между двумя или более элементами. В математике мы часто используем отношения для описания взаимосвязей между объектами или событиями. Как это можно представить? Давай посмотрим на примеры!
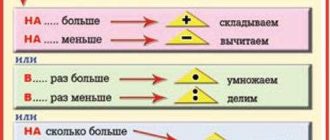
- Можем ли мы сказать, что 5 больше, чем 3? Да, это отношение «больше».
- Что насчет отношения «равно»? Мы можем сказать, что 2 равно 2.
- Или возьмем отношение «ближе». Можем ли мы сказать, что точка A ближе к точке B, чем к точке C? Тут все зависит от расстояний, можешь проанализировать и выбрать верное утверждение.
Возможных отношений может быть очень много! Они могут быть числовыми или геометрическими, качественными или количественными. Важно помнить, что отношение может быть односторонним или взаимным. Например, если относиться к отношению «больше», то оно одностороннее, потому что 5 больше 3, но не наоборот. Отношение «равно» же является взаимным, потому что два числа равны только тогда, когда они одинаковы.
Но для решения математических задач нам необходимо уметь представлять отношения не только в словесной форме, но и с использованием графических моделей. Это позволяет нам более ясно и наглядно представить взаимосвязи между элементами.
| Отношение | Графическая модель |
|---|---|
| «Больше» |
|
| «Равно» |
|
Вот так легко можно представлять отношения с помощью графических моделей! Они помогают нам лучше понять их структуру и особенности.
Запомни, отношение это неотъемлемая часть математики. Они помогают нам понять взаимодействие объектов и явлений, а также решать задачи различной сложности. Так что не бойся отношений, они всегда готовы помочь нам раскрыть новые математические горизонты!
Способы представления отношений
Один из самых простых способов представления отношений — это через таблицы. Мы можем создать таблицу, в которой в строках будут указаны элементы одного множества, а в столбцах — элементы другого множества. Затем в ячейках таблицы мы указываем, какие элементы из первого множества находятся в отношении с элементами из второго множества. Это позволяет наглядно представить, какие элементы связаны и какие нет.
Другим способом представления отношений является диаграмма Венна. Диаграмма Венна представляет собой геометрическую фигуру, обозначающую множества, и пересечения этих фигур, обозначающие элементы, находящиеся в отношении друг с другом. Этот способ особенно полезен, когда мы имеем дело с отношениями, которые имеют пересечения или общие элементы.
Еще один способ представления отношений — это формула. В математике мы часто используем формулы для описания различных связей и зависимостей между элементами. Формулы позволяют нам выразить отношения с помощью математических символов и операций, что делает их более точными и формальными.
Кроме того, отношения могут быть представлены с помощью графов. Граф представляет собой набор вершин и ребер, где вершины соответствуют элементам множеств, а ребра — отношениям между этими элементами. Графы позволяют нам визуализировать отношения и анализировать их свойства с помощью различных алгоритмов и методов.
Таким образом, существует несколько способов представления отношений в математике, каждый из которых имеет свои преимущества и применимость в различных ситуациях. Выбор способа зависит от конкретной задачи и целей, которые мы пытаемся достичь. Важно уметь выбирать и применять подходящий метод для анализа и описания отношений, чтобы получить более глубокое понимание их свойств и характеристик.
Классификация отношений
1. Бинарные отношения
Бинарные отношения являются самым простым и распространенным типом отношений. Они связывают пару элементов, принадлежащих двум множествам. Например, отношение «больше» между числами 5 и 2 является бинарным отношением. Мы можем представить бинарные отношения в виде упорядоченных пар значений.
2. Рефлексивные отношения
Рефлексивные отношения характеризуются свойством того, что каждый элемент множества связан сам с собой. Например, отношение «равно» является рефлексивным, так как каждое число равно самому себе.
3. Симметричные отношения
Симметричные отношения означают, что если элемент A связан с элементом B, то элемент B также связан с элементом A. Например, отношение «равно» является симметричным, так как если число A равно числу B, то число B также равно числу A. Это создает симметричность в отношении.
4. Транзитивные отношения
Транзитивные отношения определяются тем, что если элемент A связан с элементом B, и элемент B связан с элементом C, то элемент A также связан с элементом C. Например, если у нас есть отношение «мать» и «дочь», и затем отношение «дочь» и «внучка», то мы также можем установить отношение «мать» и «внучка» через транзитивность отношений.
5. Эквивалентные отношения
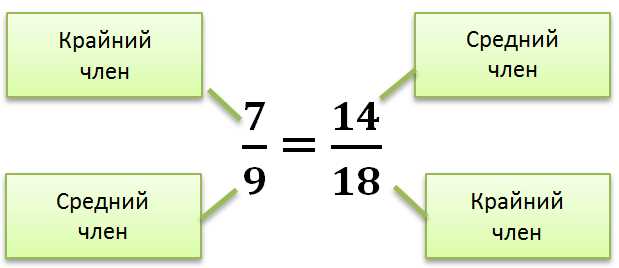
Эквивалентные отношения характеризуются свойством рефлексивности, симметричности и транзитивности. Они разбивают множество на эквивалентные классы, где все элементы в каждом классе связаны друг с другом, но не связаны с элементами из других классов. Например, отношение «равно» может быть классифицировано как эквивалентное отношение, так как числа, равные между собой, образуют эквивалентный класс.
Операции с отношениями
Одной из основных операций с отношениями является объединение. Эта операция позволяет объединить два отношения в одно, включающее все элементы из обоих множеств. Например, если у нас есть отношения «больше» и «меньше», объединение этих отношений будет содержать все пары чисел, где одно число больше или меньше другого.
Другой важной операцией с отношениями является пересечение. Она позволяет нам найти только те элементы, которые принадлежат одновременно двум отношениям. Например, если у нас есть отношения «студенты, у которых есть высокие оценки» и «студенты, которые хорошо спорят», пересечение этих отношений будет содержать только те студенты, которые сочетают оба этих качества.
Дополнение — это операция, позволяющая найти элементы, которые принадлежат одному отношению, но не принадлежат другому. Например, если у нас есть отношение «люди, которые читают книги» и «люди, которые смотрят фильмы», дополнение этого отношения будет содержать только тех, кто читает книги, но не смотрит фильмы.
Композиция или составление — это операция, которая позволяет нам создавать новое отношение путем объединения двух отношений. Например, если у нас есть отношение «студенты, которые посещают лекции» и «студенты, которые выполняют домашние задания», композиция этих отношений будет содержать все пары студентов, которые одновременно посещают лекции и выполняют домашние задания.
Операции с отношениями играют важную роль в алгебре, теории множеств, теории графов и других областях математики. Они позволяют нам анализировать и расширять знания о связях между объектами, исследовать их схожесть и различия, а также использовать эти знания в решении задач.
Итак, операции с отношениями — это мощный инструмент, который помогает нам лучше понять и описать взаимосвязи между элементами двух множеств. Они позволяют нам производить различные комбинации отношений, исследовать их свойства и применять их в различных задачах. Эти операции играют важную роль в математике и помогают нам расширять наши знания и аналитические способности. Какие операции с отношениями вы уже знаете и как они могут быть полезны вам повседневной жизни? Теперь вы знаете, что такое операции с отношениями и как их использовать в математике.
Отношение в математике: как решать и что это такое
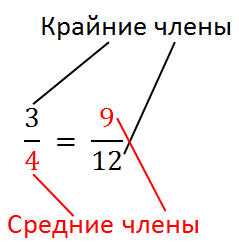
Отношения в математике могут иметь различные свойства и характеристики, их можно классифицировать на основе этих характеристик. Вот некоторые основные типы отношений:
- Рефлексивное отношение: каждый элемент множества A связан с самим собой.
- Симметричное отношение: если элемент a из A связан с элементом b из B, то элемент b также связан с элементом a.
- Антисимметричное отношение: если элемент a из A связан с элементом b из B и элемент b связан с элементом a, то a равно b.
- Транзитивное отношение: если элемент a из A связан с элементом b из B и элемент b связан с элементом c из C, то элемент a также связан с элементом c.
Для решения задач на отношения в математике необходимо понять, какие отношения заданы между элементами и как использовать эти отношения для получения нужной информации. Можно использовать таблицы или диаграммы, чтобы визуализировать отношения и проанализировать их свойства.