
Когда мы говорим о математике, одним из ключевых понятий, о котором нельзя не упомянуть, является отображение. Часто мы встречаемся с этим термином, но что же он означает? Отображение — это своего рода соответствие между двумя множествами, где каждому элементу одного множества сопоставляется элемент из другого множества.
Хотите понять это на практике? Возьмем в качестве примера карту города. Эта карта отображает реальный город, где каждое здание или улица на карте соответствуют конкретному объекту в городе. Таким образом, каждый элемент — здание или улица — на карте отображается на реальный объект в городе.
Таким образом, отображение — это невероятно важная концепция в математике, которая помогает нам понять связи и соотношения между различными объектами и явлениями. Запустите свое воображение и начните исследовать мир отображений вместе с нами!
Отображение в математике
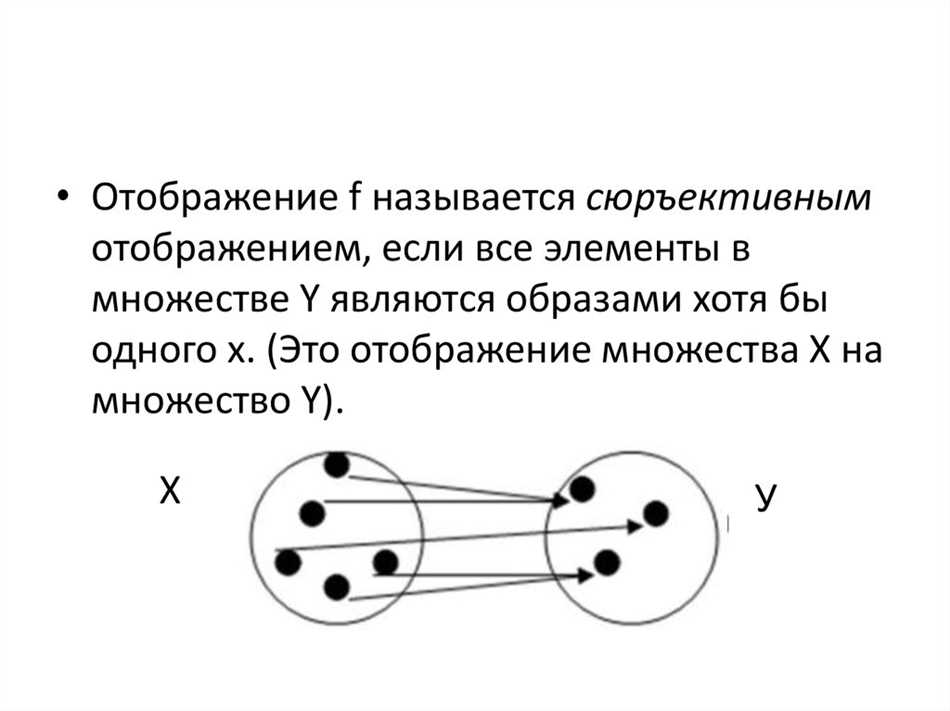
Концепция отображения может быть понятна лучше на примере. Рассмотрим простой пример отображения между множествами A и B:
- A = {1, 2, 3}
- B = {a, b, c}
Мы можем определить отображение, которое называется f, следующим образом:
- f(1) = a
- f(2) = b
- f(3) = c
Таким образом, мы устанавливаем связь между элементами A и B, где каждому элементу из A соответствует определенный элемент из B. В данном случае, отображение f переводит число 1 в букву a, число 2 в букву b и число 3 в букву c.
Отображения могут быть выражены различными способами. Они могут быть заданы списком или таблицей, как в примере выше, или с помощью формулы или алгоритма, определяющего связь между элементами двух множеств.
Отображения играют важную роль в математике, так как они позволяют нам изучать связи между различными множествами и устанавливать соответствия между элементами. Они также имеют много применений в других областях, включая физику, информатику и экономику.
Теперь, когда вы знаете, что такое отображение в математике, вы можете легче понять его роль и значение в различных математических концепциях и задачах. Задайте себе вопрос: какие отображения вы можете найти в своей повседневной жизни? Может быть, соответствие между вашим списком покупок и продуктами в супермаркете? Или соответствие между номерами телефонов и их владельцами в вашей телефонной книге?
Определение отображения
Возможно, вы задаетесь вопросом, что именно я имею в виду, говоря о «связи» между элементами множеств. Давайте рассмотрим простой пример. Представьте себе два множества: множество всех людей с их именами и множество всех городов с их названиями. Мы можем сопоставить каждому человеку его родной город. Это и есть пример отображения, где каждому элементу из одного множества сопоставляется элемент из другого множества.
Когда мы говорим о отображении, мы обычно говорим о функции, что является особым случаем отображения. Функция — это отображение, где каждому элементу из одного множества сопоставляется только один элемент из другого множества. Например, функцией может быть отображение, которое каждому числу сопоставляет его квадрат.
Отображение можно представить в виде специальной таблицы, называемой таблицей отображения. В этой таблице элементы первого множества представлены в одном столбце, а элементы второго множества — в другом столбце. Каждой паре элементов из этих столбцов можно сопоставить стрелку, указывающую на соответствующее отображение. Например, в таблице отображения для функции, отображающей каждое число на его квадрат, в первом столбце будут числа, а во втором столбце — квадраты этих чисел.
Отображения имеют множество практических применений в различных областях науки и техники. Они могут помочь в моделировании сложных систем, оптимизации процессов, решении уравнений и многих других задачах. Изучение отображений позволяет увидеть связи и зависимости между различными объектами и явлениями, что помогает нам лучше понять окружающий мир.
Определение отображения
Представь, у тебя есть два множества: множество A, где находятся все ученики твоего класса, и множество B, где находятся все их имена. Отображение будет представлять собой связь между учениками и их именами: каждому ученику из множества A будет поставлено в соответствие его имя из множества B. Итак, каждый ученик имеет свое имя, и мы можем однозначно определить, кому принадлежит каждое имя.
Теперь я бы хотел показать тебе несколько примеров отображений, чтобы ты лучше представлял себе, что это такое:
- Отображение между множеством целых чисел и их квадратами: каждому числу будет поставлено в соответствие его квадрат. Например, число 2 будет отображено в число 4 (2 * 2 = 4).
- Отображение между множеством студентов и их оценками: каждому студенту будет поставлена в соответствие его оценка. Например, студент Джон будет отображен на оценку 90.
- Отображение между множеством городов и их столицами: каждому городу будет поставлена в соответствие его столица. Например, Москва будет отображена на Москву.
Убедительно, правда? Теперь ты знаешь, что такое отображение в математике. И помни, отображение может быть очень полезным инструментом при решении различных задач и анализе данных. Приятного путешествия в мир отображений!
Примеры отображений
В математике существуют различные примеры отображений, которые помогают нам лучше понять, как они работают и как их можно применять в различных областях.
Одним из примеров отображений является функция, которая является одним из самых основных понятий в математике. Функция преобразует одно значение (аргумент) в другое значение (значение функции). Например, функция f(x) = 2x обозначает, что каждому числу x соответствует число 2x. Если x = 3, то f(3) = 2 * 3 = 6. Таким образом, мы преобразовали значение x в значение f(x).
Еще одним примером отображений является матрица. Матрица в математике — это таблица, состоящая из чисел или переменных, разделенных на строки и столбцы. Матрицы широко используются в линейной алгебре, физике, экономике и других науках. Например, матрица может представлять систему уравнений или операцию, выполняемую над векторами.
Отображения также могут применяться в геометрии. Например, отображение может преобразовывать фигуру на плоскости, такую как треугольник, в другую фигуру, например, прямоугольник. Это отображение может быть основано на изменении масштаба, повороте или сдвиге. Такие отображения помогают нам понять различные свойства геометрических фигур и их преобразования.
Также отображения можно применять в комбинаторике, теории множеств и других областях математики. Они позволяют установить соответствие между различными объектами и изучать их свойства.
Свойства отображений
Свойство 1: Определенность
Первым важным свойством отображений является их определенность. Определенность означает, что каждому элементу из первого множества сопоставлен какой-то элемент из второго множества. Иначе говоря, отображение должно быть определено для каждого элемента исходного множества.
Например, рассмотрим отображение «f: множество натуральных чисел -> множество четных чисел», которое каждому натуральному числу сопоставляет его удвоенное значение. В этом случае, отображение определено для каждого натурального числа.
Свойство 2: Однозначность
Однозначность является ключевым свойством отображений. Она гарантирует, что каждому элементу из первого множества сопоставлен только один элемент из второго множества. Это означает, что двум разным элементам из первого множества нельзя сопоставить один и тот же элемент из второго множества.
Например, рассмотрим отображение «g: множество целых чисел -> множество квадратов». Данное отображение каждому целому числу сопоставляет его квадрат. Оно является однозначным, так как каждому целому числу сопоставлен только один квадрат.
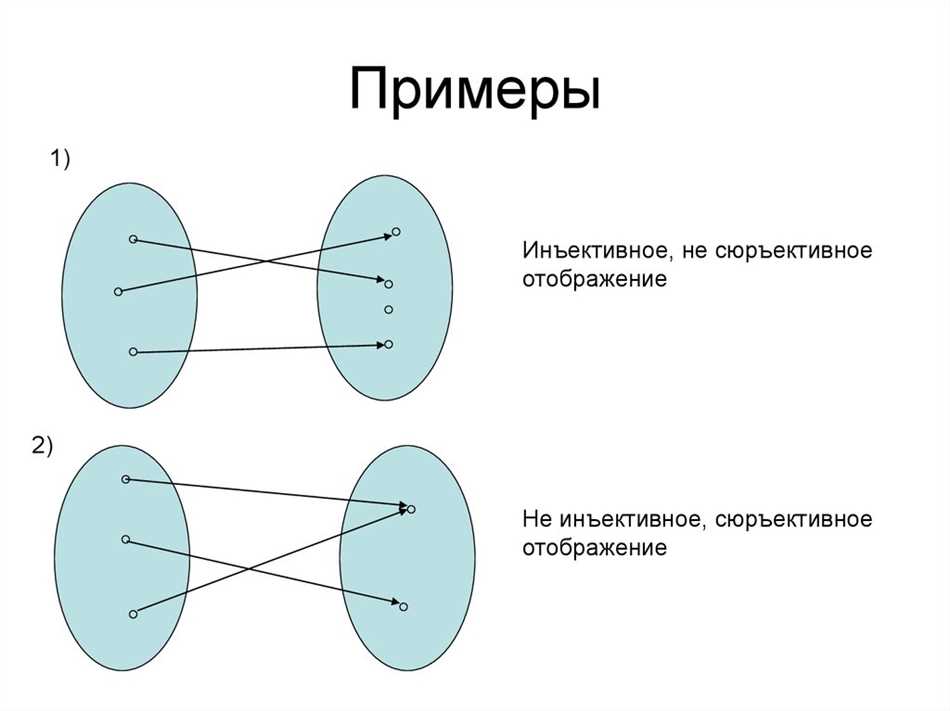
Свойство 3: Сюръективность
Сюръективность отображения означает, что для каждого элемента из второго множества найдется хотя бы один элемент из первого множества, который ему соответствует. Иными словами, отображение переводит каждый элемент из второго множества на попарно различные элементы из первого множества.
Например, рассмотрим отображение «h: множество действительных чисел -> множество неотрицательных чисел», которое каждому действительному числу сопоставляет его квадрат. Это отображение является сюръективным, так как для каждого неотрицательного числа найдется действительное число, его квадрат.
Свойство 4: Инъективность
Инъективность отображения означает, что каждому элементу из второго множества соответствует не более одного элемента из первого множества. Иначе говоря, разным элементам из второго множества должны соответствовать разные элементы из первого множества.
Например, рассмотрим отображение «k: множество действительных чисел -> множество интервалов». Данное отображение каждому действительному числу сопоставляет интервал вида (x, x+1). Оно является инъективным, так как разным действительным числам соответствуют разные интервалы.
Важно помнить, что отображения могут обладать комбинацией свойств. Например, они могут быть одновременно и сюръективными и инъективными, что их делает биекциями.
Инъективность
Ура! Мы продолжаем наше путешествие в мир отображений! Сегодня я хочу рассказать тебе о понятии «инъективность». Это очень интересное свойство отображения, которое может быть полезно в разных областях науки и жизни.
Инъективность — это свойство отображения, когда каждому элементу из области определения соответствует уникальный элемент из области значений. Другими словами, если у нас есть два разных элемента из области определения, то они будут иметь разные образы в области значений.
Представь, что у нас есть группа людей, и мы хотим сопоставить каждому человеку его уникальный идентификатор. Если у нас есть отображение, которое выполняет это задание, то оно может быть инъективным. То есть каждому человеку будет соответствовать уникальный идентификатор, и никакие два разных людей не будут иметь одинаковых идентификаторов.
Инъективность может быть полезной в таких областях, как криптография и базы данных. Например, в криптографии мы можем использовать инъективные отображения для обеспечения безопасности передачи информации. Если каждому символу исходного сообщения соответствует уникальный зашифрованный символ, то это ersatz rambler-а продуктаlers
Именно поэтому инъективные отображения обычно называют «инъекциями». Их можно представить себе как шприц, который вводит элементы из области определения в область значений без потерь или дублирования.
Вот, пожалуй, и все, что я хотел рассказать тебе о инъективности в математике! Надеюсь, ты нашел этот материал интересным и полезным. А теперь я задам тебе вопрос: можешь ли ты привести примеры инъективных отображений из своей повседневной жизни?
Отображение в математике: определение и примеры
Отображение обычно обозначается символом «f» и записывается в виде f: A → B, где A и B — множества, причем A — множество исходных элементов, B — множество образов. Для каждого элемента a из множества A, правило отображения f ставит в соответствие элемент b из множества B.
Примеры отображений:
- f(x) = x^2, где A и B — множества действительных чисел. Правило отображения f ставит в соответствие каждому элементу из множества действительных чисел его квадрат.
- g(x) = 2x + 1, где A и B — множества действительных чисел. Правило отображения g ставит в соответствие каждому элементу из множества действительных чисел удвоенное значение с добавлением единицы.




