Отсчетный эллипсоид и его значение в геодезии

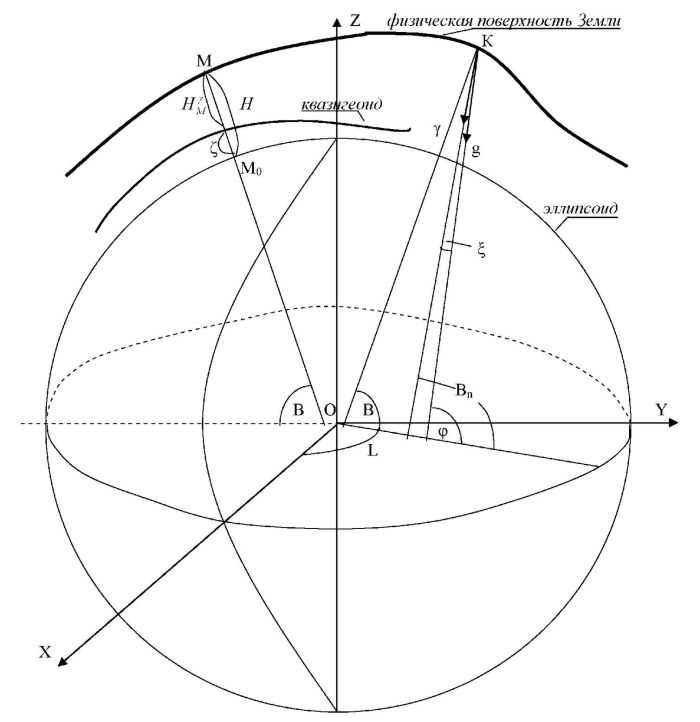
Если вы интересуетесь геодезией, то наверняка слышали о понятии «отсчетный эллипсоид». И это не просто еще один термин из теории геодезии – это очень важный инструмент, который играет ключевую роль в определении географических координат точек на Земле.

О чем идет речь? Отсчетный эллипсоид – это модель Земли, которая представляет ее в виде эллипсоида. Понимание его формы и размеров позволяет геодезистам точно определять координаты местоположения объектов, а также проводить геодезические измерения и геодезическую съемку. Как правило, используются различные эллипсоиды в разных странах и регионах.

Таким образом, понимание отсчетного эллипсоида – это необходимое условие для достижения точных результатов при проведении геодезических работ. В данной статье мы рассмотрим, что представляет собой отсчетный эллипсоид, как он используется в геодезии, и почему он играет такую важную роль в этой науке.

Что такое отсчетный эллипсоид?

Отсчетный эллипсоид — это модель Земли, приближенное представление ее формы в виде эллипсоида. Мы знаем, что Земля имеет достаточно сложную форму, не похожую на идеальный шар. Вместо этого ее форма ближе к эллипсоиду, то есть она вытянута по полюсам и сплюснута у экватора.

Зачем нам нужна такая модель? Дело в том, что для проведения геодезических измерений и определения координат точек на Земле, нам необходимо иметь некую систему отсчета. С помощью отсчетного эллипсоида мы можем задавать точные координаты точек и применять их в геодезических расчетах.

Интересно то, что в мире существует несколько разных моделей отсчетных эллипсоидов, каждая из которых имеет свои параметры и характеристики. Например, для России и бывших советских стран используется отсчетный эллипсоид Красовского.

Мы уже говорили о том, что отсчетный эллипсоид позволяет нам определить координаты точек на Земле, но каким образом это происходит? Для этого используется система геодезических координат, которая включает в себя широту, долготу и высоту над уровнем моря. Благодаря этой системе каждая точка на Земле может быть однозначно определена.

Таким образом, отсчетный эллипсоид становится неотъемлемой частью геодезии и позволяет нам осуществлять точные измерения и определения координат нашей планеты. Это важное понятие помогает установить связь между геодезическими измерениями и картографией, позволяет создавать точные карты и навигационные системы.

Каково значение отсчетного эллипсоида в геодезии?

Значение отсчетного эллипсоида состоит в том, что он позволяет определить географические координаты любой точки на Земле с высокой точностью. Благодаря этому, инженеры и геодезисты могут строить карты, проводить геодезические измерения, определять площади, длины и высоты объектов, а также навигировать в пространстве.

Отсчетный эллипсоид является основой для геодезической системы координат, которая широко используется в современной геодезии и геодезической геодинамике. Он образует главную основу для определения широты, долготы и высоты точек на Земле.

Точность определения координат очень важна во многих областях, таких как строительство, навигация, астрономия и топография. Например, при строительстве дорог, мостов и зданий необходимо точно определить местоположение объектов относительно друг друга. Точное измерение координат позволяет избежать ошибок и повысить качество выполнения работ.

В геодезии отсчетный эллипсоид служит базой для определения геодезической высоты. Геодезическая высота определяется относительно эллипсоида и показывает разницу между геометрической высотой объекта и поверхностью отсчетного эллипсоида. Это важная информация для строительства уровней, каналов и других инженерных сооружений.

Кроме того, отсчетный эллипсоид позволяет определить геоидальную аномалию, которая является разницей между фактической формой Земли и ее идеальным математическим представлением. Измерение геоидальной аномалии имеет особое значение, так как позволяет более точно определить форму Земли и проводить расчеты в геодезии и геофизике.

В итоге, значение отсчетного эллипсоида в геодезии не может быть переоценено. Он обеспечивает точность определения координат, позволяет проводить измерения и расчеты, а также совершенствовать геодезические методы. Благодаря отсчетному эллипсоиду геодезисты и инженеры могут достичь высокой точности и точности в своей работе.

Отсчетный эллипсоид как геометрическая модель Земли

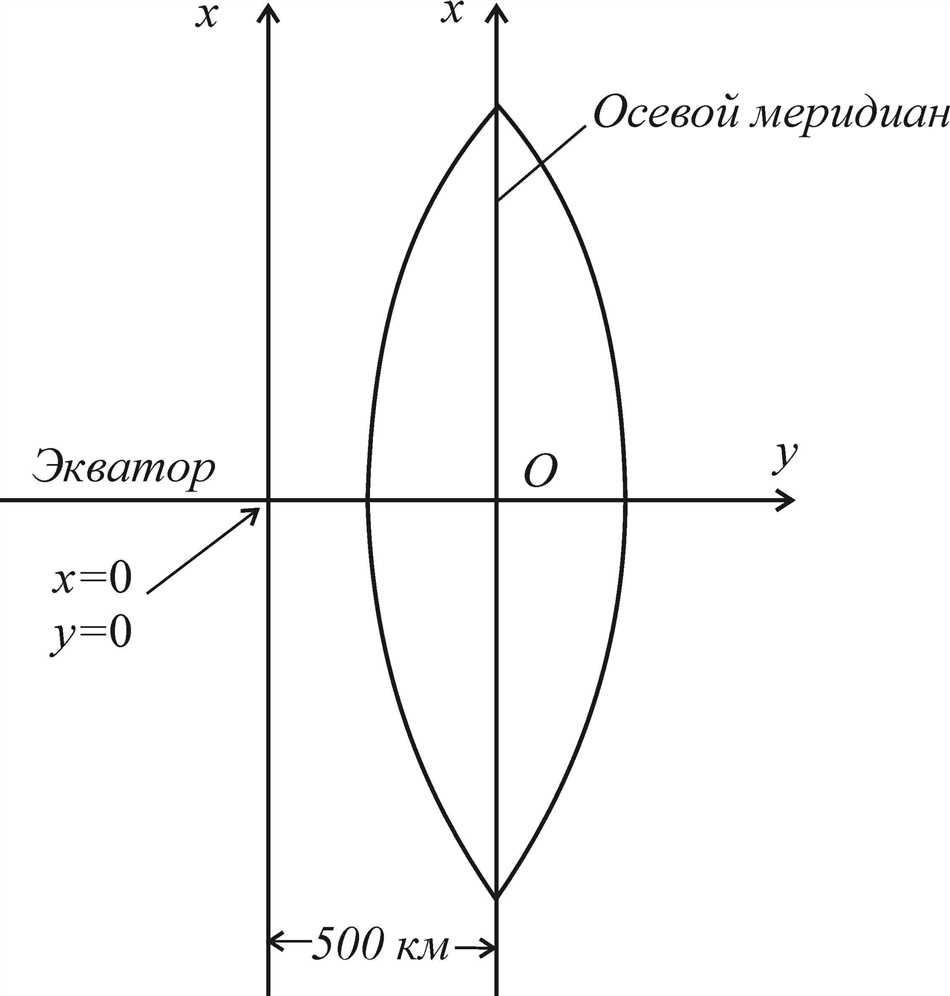
Вот где на сцену выходит отсчетный эллипсоид, геометрическая модель Земли, которая помогает нам изучать ее форму и размеры. Отсчетный эллипсоид является аппроксимацией формы Земли и представляет собой эллипс, вращающийся вокруг своей оси. Благодаря этой модели мы можем легко описывать и измерять точки на поверхности Земли.

Теперь вы можете задать вопрос: зачем нам нужна эта модель? Почему мы не можем просто измерить расстояние между двумя точками? Ответ прост: Земля — огромная планета с неравномерным геометрическим профилем. Если мы не используем модель, мы не сможем учесть изгиб поверхности Земли и получим неточные результаты.

Отсчетный эллипсоид также включает в себя систему координат, которая позволяет нам точно определить местоположение точки на Земле. Эти координаты используются в геодезии, науке, изучающей Землю и ее форму.

Итак, отсчетный эллипсоид — это не просто геометрическая модель Земли, он является ключом к пониманию формы и размеров нашей планеты. Благодаря ему мы можем точно измерять расстояния и определять местоположение на Земле. Отсчетный эллипсоид — это инструмент, который помогает нам исследовать и понимать наш дом — планету Земля.

Определение геодезических координат на отсчетном эллипсоиде

Перед определением геодезических координат необходимо выбрать отсчетный эллипсоид, на котором будут производиться измерения. Отсчетный эллипсоид — это упрощенная модель земной поверхности, представляющая собой эллипсоид реверсного обращения вращения, который наилучшим образом соответствует форме Земли.

Когда отсчетный эллипсоид выбран, можно переходить к определению геодезических координат. Это делается посредством специальных методов измерения, таких как GPS, геодезическое астрономическое определение или геодезическая триангуляция.

Процесс определения геодезических координат на отсчетном эллипсоиде включает несколько шагов. Сначала определяется широта, которая измеряется в градусах, минутах и секундах или в десятичных градусах. Это делается с помощью спутниковой навигационной системы GPS или путем наблюдения за звездами или солнцем.

Затем определяется долгота, которая также измеряется в градусах, минутах и секундах или в десятичных градусах. Для этого используется такая же система GPS или астрономические методы.

В конце процесса определяется высота, которая измеряется относительно поверхности отсчетного эллипсоида. Высота может быть измерена с помощью GPS или специальных геодезических инструментов, таких как нивелир или теодолит.

Таким образом, определение геодезических координат на отсчетном эллипсоиде требует выполнения нескольких шагов, каждый из которых включает использование специальных инструментов и методов измерения. Эта информация позволяет геодезистам точно определить положение объектов на земной поверхности и использовать ее, например, при создании карт, навигации и планировании строительства.

Основные характеристики отсчетного эллипсоида

Одной из основных характеристик отсчетного эллипсоида является его направляющий радиус, который определяет расстояние от центра эллипсоида до точки на его поверхности. Направляющий радиус также называется главным радиусом кривизны и играет важную роль в геодезии.

Другой важной характеристикой является эксцентриситет эллипсоида, который определяет степень его сжатия относительно сферы. Эксцентриситет позволяет учесть несовпадение между моделью эллипсоида и истинной формой Земли, что влияет на точность геодезических измерений.

Также следует отметить угловой радиус кривизны отсчетного эллипсоида, который определяется по формуле: R = a * (1 — e^2), где a — большая полуось эллипсоида, e — его эксцентриситет. Угловой радиус кривизны позволяет оценить кривизну геодезической кривой, то есть линии, которая наиболее полно описывает форму поверхности Земли в данной точке.

Еще одной важной характеристикой отсчетного эллипсоида является его гравитационный потенциал. Гравитационный потенциал позволяет определить силу притяжения, которая действует на объекты на поверхности Земли. Гравитационный потенциал зависит от массы Земли и ее формы, которую описывает отсчетный эллипсоид.

Наконец, важно отметить, что отсчетный эллипсоид имеет свои особенности в зависимости от конкретной модели, например, WGS 84 или PZ-90. Каждая модель имеет свои коэффициенты эксцентриситета и другие параметры, которые определяют ее форму и размеры.

Таким образом, основные характеристики отсчетного эллипсоида включают направляющий радиус, эксцентриситет, угловой радиус кривизны, гравитационный потенциал и специфические параметры модели. Понимание этих характеристик важно для проведения точных геодезических измерений и определения географических координат на поверхности Земли.

Большая и малая полуоси

Большая полуось (a) является расстоянием от центра эллипсоида до его самой длинной точки, которая находится на его поверхности. Этот параметр обозначает размер эллипсоида и называется «большой», потому что он является наибольшим из всех полуосей. Большая полуось важна для определения формы Земли и используется при создании глобальных моделей и карт.

Малая полуось (b) представляет собой расстояние от центра эллипсоида до его самой короткой точки на поверхности. Она перпендикулярна к большой полуоси и обозначает сжатие эллипсоида в поперечном направлении. Малая полуось позволяет учитывать эффекты ротации Земли и аномалии силы тяжести. Она также используется в геодезических расчетах для определения точных координат и высотных отметок.

Знаете ли вы, что значения большой и малой полуосей отличаются в разных системах координат и геодезических моделях? Например, в системе WGS-84 (World Geodetic System 1984), которая широко используется в навигационных приборах и Системе Глобального Позиционирования (GPS), значения большой и малой полуосей составляют примерно 6 378 137 метров и 6 356 752 метра соответственно. Отличия в этих значениях могут привести к погрешности в измерениях и расчетах.

Итак, большая и малая полуоси являются существенными параметрами отсчетного эллипсоида и определяют его форму и размер. Они жизненно важны для корректных геодезических расчетов и построения геодезических моделей. Помните, что эти значения могут различаться в разных системах координат, поэтому важно знать, какая система используется в ваших геодезических измерениях и расчетах.

Эксцентриситет и другие параметры

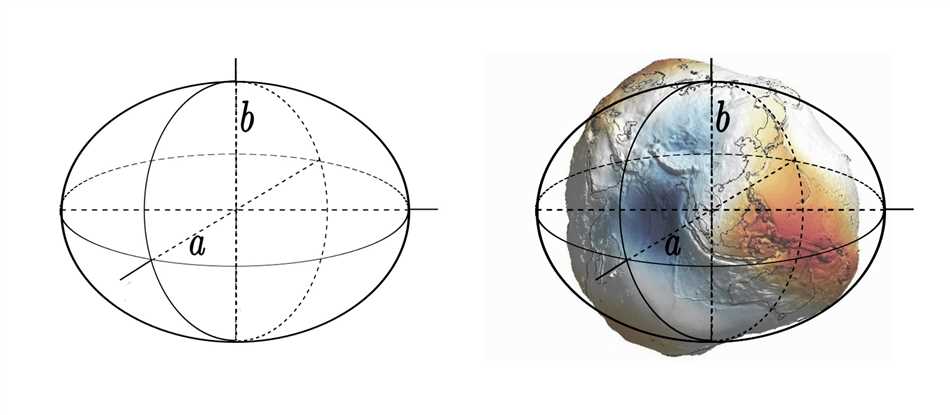
Эксцентриситет можно представить в виде числа от 0 до 1. Если эксцентриситет равен 0, это значит, что эллипсоид является сферой. Если эксцентриситет стремится к 1, то форма эллипсоида становится все более вытянутой, похожей на овал.

Еще одним важным параметром отсчетного эллипсоида является большая полуось. Это расстояние от центра эллипсоида до его наружной границы вдоль оси, которая имеет наибольшую длину. Большая полуось обозначается символом «a». Зная значение большой полуоси, мы можем определить размеры и форму эллипсоида.

Кроме того, существует также малая полуось, которая обозначается символом «b». Малая полуось является перпендикулярной к большой полуоси и определяет размер эллипсоида вдоль его второй оси.

Однако, для полного определения формы эллипсоида нам нужно еще одно значение — геоцентрическая сводная растворенность. Это параметр, который отражает распределение массы Земли и физическую форму эллипсоида. Он обозначается символом «α». Геоцентрическая сводная растворенность также влияет на гравитацию на поверхности Земли.

Все эти параметры — эксцентриситет, большая и малая полуоси, геоцентрическая сводная растворенность — совместно определяют форму и размеры отсчетного эллипсоида. Когда мы знаем эти значения, мы можем использовать их для геодезических измерений, чтобы определить точное географическое положение любой точки на поверхности Земли.

Отсчетный эллипсоид и его значение в геодезии

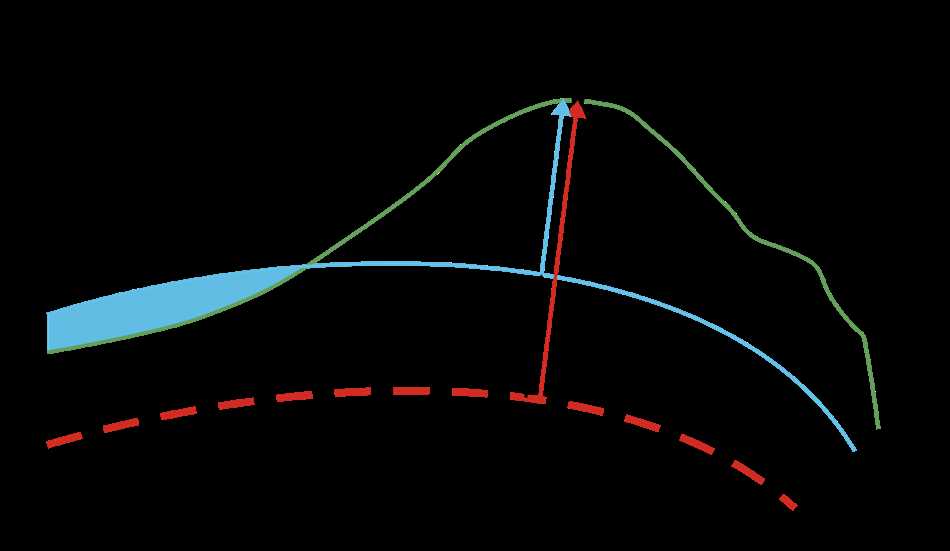
Отсчетный эллипсоид имеет определенные параметры, такие как полуось a (большая полуось эллипсоида) и сжатие эллипсоида f. Эти параметры позволяют определить форму эллипсоида и его соответствие реальной форме Земли. Альтернативной формой параметризации является обратное сжатие эллипсоида 1/f.

Значение отсчетного эллипсоида в геодезии заключается в том, что с его помощью определяются географические координаты точек на Земле. Геодезическая система координат включает в себя прямоугольную систему (геоцентрическую), географическую систему (геодезическую) и местную систему координат (картографическую).

Отсчетный эллипсоид используется для создания карт и планов, а также для определения расстояний, направлений и площадей на Земле. Он позволяет проводить точные измерения и определять координаты точек с высокой точностью.