Наверное, каждый из нас помнит, как мы в школе изучали геометрию и строили треугольники. И одним из важных свойств треугольника является то, что его средняя линия параллельна основанию.
Но почему это так?
Основание треугольника — это одна из его сторон, на которой он «стоит». Именно она является опорной точкой, вокруг которой строится весь треугольник. А средняя линия — это отрезок, соединяющий середины двух сторон треугольника. При этом средняя линия делит основание на две равные части.
Поэтому, чтобы средняя линия была параллельна основанию, необходимо, чтобы середины сторон треугольника лежали на одной прямой, а это возможно только при равенстве длин этих сторон. Таким образом, средняя линия треугольника параллельна основанию, если треугольник равнобедренный.
Свойство треугольника

Знаешь ли ты, что треугольники могут быть очень удивительными? Они обладают различными свойствами, и одним из них я хочу поделиться с тобой. Это свойство называется «средняя линия треугольника параллельна основанию». Звучит сложно, не так ли? Но не волнуйся, я объясню это простыми словами.
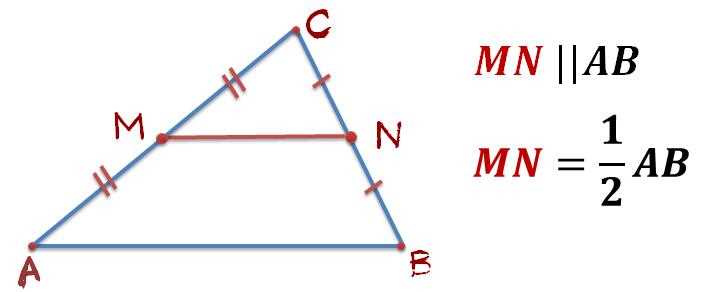
Допустим, у нас есть треугольник с вершинами A, B и C. Средняя линия треугольника — это линия, которая соединяет середины двух сторон. И вот что интересно: эта линия всегда будет параллельна основанию треугольника!
Представь себе, что у тебя есть треугольник с основанием AB и серединной линией, которая соединяет середины сторон BC и AC. Если ты проведешь эту линию, то заметишь, что она будет параллельна стороне AB. Такое свойство средней линии существует в любом треугольнике, независимо от его размеров и формы.
Это удивительно, не так ли? И это только одно из множества свойств, которыми обладают треугольники. Исследуй их дальше, и, кто знает, что интересного ты еще обнаружишь! Треугольники — это весело и увлекательно, а это свойство только добавляет им загадочности и красоты.
Определение треугольника
Во-первых, все три стороны треугольника должны быть прямыми линиями, а все его углы должны быть острыми. Но существуют и другие типы треугольников, например, равнобедренные треугольники, у которых две стороны равны, или прямоугольные треугольники, которые имеют один прямой угол.
Что же делает треугольник особенным? Во-первых, он является самой простой многоугольной фигурой. Ведь чтобы его построить, нужно всего лишь провести три линии и соединить их концы. Треугольник также является основой для изучения других геометрических фигур, таких как параллелограммы и треугольные пирамиды.
Знаете ли вы, что все треугольники имеют сумму углов равную 180 градусов? Здесь есть много интересных математических закономерностей на эту тему, с которыми можно поиграть и исследовать.
Основные свойства треугольника
- Сумма углов треугольника: Всегда при любых значениях углов сумма углов внутри треугольника равна 180 градусам.
- Типы треугольников: В зависимости от длин сторон и значений углов, треугольники могут быть разных типов: равносторонние (все стороны равны), равнобедренные (две стороны равны), прямоугольные (имеют прямой угол) и т. д.
- Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон.
- Высоты треугольника: Треугольник может иметь три высоты – перпендикуляры, опущенные из вершин к противоположным сторонам. Важно отметить, что высоты могут пересекаться в одной точке, называемой ортоцентром.
- Серединные перпендикуляры: Проведя серединные перпендикуляры ко всем сторонам треугольника, они пересекутся в одной точке, называемой центром окружности, вписанной в треугольник.
Вот только некоторые из основных свойств треугольника. Он является одной из основных фигур в геометрии, и изучение его свойств позволяет лучше понять мир вокруг нас. Математика – это удивительно!
Параллельные линии

Когда мы говорим о средней линии треугольника, мы имеем в виду линию, которая соединяет середины двух сторон треугольника. Важно отметить, что эта линия всегда параллельна основанию треугольника. Это происходит потому, что стороны треугольника, которые соединяются с помощью средней линии, параллельны друг другу. Таким образом, средняя линия треугольника будет иметь ту же направленность и останется на одном и том же расстоянии от основания во всех точках.
Параллельные линии играют важную роль в геометрии и имеют множество применений в повседневной жизни. Они используются в архитектуре, при построении дорог, в дизайне и многих других областях. Параллельные линии помогают создавать симметрию и порядок, а также облегчают измерение и построение объектов.
Определение средней линии треугольника
Возможно, ты замечал, что в треугольнике средняя линия, проведенная из одной стороны до противоположного угла, всегда параллельна основанию. Это довольно интересное свойство треугольников, и оно помогает нам лучше понять их структуру и геометрию.
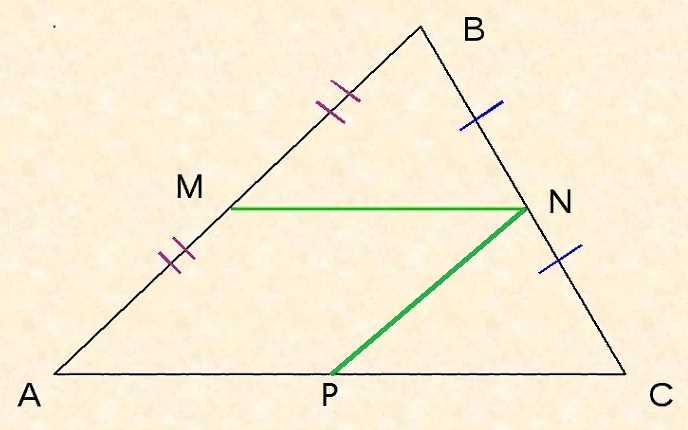
Средняя линия треугольника — это отрезок, который соединяет середину одной стороны с вершиной противоположного угла. Другими словами, если у нас есть треугольник ABC, то средняя линия, исходящая из стороны BC, соединяет точку M (середина стороны BC) с вершиной A.
Замечательно то, что средняя линия всегда будет параллельна основанию треугольника (стороне BC). Это можно доказать с помощью геометрических построений и принципов, но давай погрузимся в хитрости и уголки, чтобы не теряться в формулах!
Из чего же это следует? Поставь себя на место точки M и задумайся: если бы сторона BC и основание треугольника не были параллельны, мы бы получили странный искаженный треугольник. И это довольно неприятно. В математике нам нравятся четкие и красивые формы, поэтому средняя линия всегда параллельна основанию треугольника.
Понятие средней линии

Представь, что ты встретил треугольник на прогулке и хочешь узнать, где находится его средняя линия. Проще всего найти середины двух сторон треугольника и соединить их линией. Вот и всё! Теперь ты видишь среднюю линию треугольника.
Знаешь ли ты, почему средняя линия параллельна основанию треугольника? Это потому, что при соединении середин двух сторон мы получаем прямоугольник, и в прямоугольнике противоположные стороны параллельны. Так что средняя линия всегда будет параллельна основанию треугольника.
Запомни, что средняя линия треугольника — это особенная линия, которая не только делит треугольник на две равные части, но также имеет свойство быть параллельной одной из сторон. Всякий раз, когда ты будешь видеть треугольник, ты сможешь легко найти его среднюю линию и изучить ее свойства.