Понятие и свойства неколлинеарных векторов в геометрии 9 класс

Когда мы изучаем геометрию в 9 классе, одним из важных понятий являются векторы и их свойства. Векторы — это математические объекты, которые используются для представления направления и силы движения. Когда векторы находятся на одной прямой линии, они называются коллинеарными. Но что делать, если векторы не находятся на одной прямой линии? В таком случае они называются неколлинеарными векторами. В этом введении мы рассмотрим основные характеристики неколлинеарных векторов и их применение в геометрии.

Теория неколлинеарных векторов

Представьте себе два вектора и задайте себе вопрос: могут ли они быть находиться на одной прямой? Если ваш ответ «нет», то вы на верном пути к пониманию теории неколлинеарных векторов.

Коллинеарные векторы — это векторы, которые лежат на одной прямой. Они имеют одно и то же направление или противоположное направление. Но что насчет неколлинеарных векторов? Какова их природа и как они связаны геометрически?

Неколлинеарные векторы и треугольник

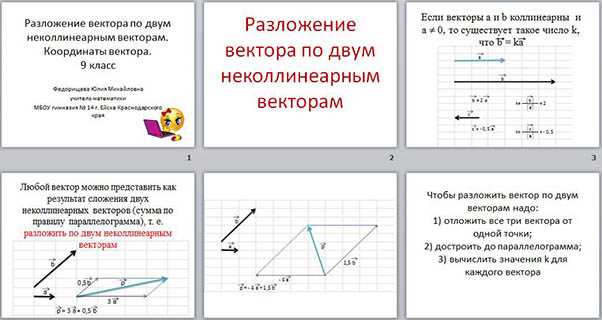
Неколлинеарные векторы — это векторы, которые не лежат на одной прямой, а значит, они образуют треугольник. Можно сказать, что неколлинеарные векторы связаны в геометрическом пространстве и помогают нам представлять их взаимосвязь.

Итак, представьте, что у вас есть три неколлинеарных вектора A, B и C. Соедините их начало в точке О и нарисуйте линии, соединяющие начало каждого вектора с концом других двух векторов. Вы получите треугольник. Этот треугольник называется векторным треугольником.

Векторный треугольник имеет некоторые особенности, которые нам могут помочь лучше понять неколлинеарные векторы. Например, сумма всех сторон векторного треугольника равна нулю. Это значит, что если мы сложим все три вектора (A + B + C), то получим нулевой вектор. Другими словами, конечная точка вектора A совпадает с началом вектора B, конечная точка вектора B совпадает с началом вектора C, а конечная точка вектора C совпадает с началом вектора A.

Приложение неколлинеарных векторов

Теперь давайте рассмотрим, как мы можем использовать неколлинеарные векторы в геометрии и математике.

• Одно из применений неколлинеарных векторов — выяснить, лежит ли точка на стороне треугольника или внутри него. Мы можем построить векторы, соединяющие вершины треугольника и данную точку, и проверить, совпадает ли их сумма с нулевым вектором.
• Неколлинеарные векторы также позволяют нам определить, является ли треугольник равносторонним, равнобедренным или общего вида. Равносторонний треугольник имеет все стороны равными, равнобедренный треугольник имеет две равные стороны, а треугольник общего вида имеет все стороны разные.
• Кроме того, неколлинеарные векторы используются в компьютерной графике для создания 3D-моделей и анимации. Они позволяют нам определить положение и направление объектов в пространстве.

Итак, теория неколлинеарных векторов помогает нам лучше понять и визуализировать взаимосвязь между векторами. Она находит свое применение в геометрии, математике и компьютерной графике. Используйте эту теорию, чтобы решать задачи и создавать новые идеи. Успехов вам в изучении геометрии!

Геометрическая интерпретация

Неколлинеарные векторы не лежат на одной прямой и имеют разные направления, но они все равно могут быть взаимосвязаны в геометрическом смысле. Геометрическая интерпретация неколлинеарных векторов позволяет визуализировать их отношение и использовать их в решении геометрических задач.

Представь себе два неколлинеарных вектора: AB и AC. Теперь представь, что начало вектора AB находится в точке А, а его конец – в точке В. Точно так же, начало вектора AC находится в точке А, а его конец – в точке С. Сейчас представь, что векторы AB и AC находятся в одной плоскости, но не лежат на одной прямой.

Векторы AB и AC могут иметь разные направления и длины, но они все равно связаны между собой. Представь, что ты соединяешь концы этих векторов. Получится некоторый треугольник, где стороны треугольника – это векторы AB и AC, а вершина треугольника – точка А.

Интересно, правда? Таким образом, геометрическая интерпретация неколлинеарных векторов позволяет наглядно представить их отношение в пространстве. Это поможет в понимании и решении различных геометрических задач. Например, можно использовать неколлинеарные векторы для нахождения середины отрезка, построения параллелограмма или определения площади треугольника.

Определение неколлинеарности векторов

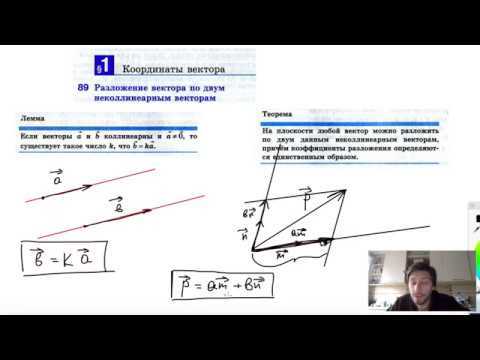
Неколлинеарные векторы в геометрии представляют собой векторы, которые не лежат на одной прямой. Коллинеарные векторы, напротив, находятся на одной прямой и могут быть представлены как кратные друг другу.

Для определения неколлинеарности двух векторов, мы можем использовать следующий метод: сначала рассчитываем векторное произведение этих векторов и затем проверяем, равно ли оно нулю. Если векторное произведение равно нулю, то векторы являются коллинеарными. А если векторное произведение не равно нулю, то векторы неколлинеарны.

Примером неколлинеарных векторов может служить рассмотрение двух векторов, например, AB и AC, где точка A является началом обоих векторов, а точки B и C — их концами. Если векторное произведение векторов AB и AC не равно нулю, то эти векторы неколлинеарны, а их концы лежат на разных прямых.

Неколлинеарные векторы часто исследуются в геометрии, так как они обладают важными свойствами и применяются в различных математических и физических задачах. Они позволяют определить точные углы и расстояния между точками, а также рассчитать площади параллелограммов и треугольников.

Понимание неколлинеарности векторов поможет нам лучше понять и применять геометрические концепции и методы в различных областях науки, включая физику, инженерию и компьютерную графику. Зная, как определить неколлинеарность векторов, мы сможем решать сложные математические задачи и использовать их в реальных сценариях и ситуациях.

Способы проверки неколлинеарности

В геометрии неколлинеарность означает, что заданные векторы не лежат на одной прямой. Это важное понятие, которое помогает нам анализировать и понимать пространственные отношения между векторами. Существует несколько способов проверки неколлинеарности, которые могут быть полезны в решении геометрических задач. Давайте рассмотрим некоторые из них.

1. Геометрическая проверка

Один из способов проверки неколлинеарности векторов — это сравнение их направлений и длин. Если два вектора имеют разные направления и не равны по длине, то они, скорее всего, будут неколлинеарны. Например, если у нас есть векторы AB и AC, то мы можем сравнить их направления и длины, чтобы понять, лежат ли они на одной прямой или нет.

2. Аналитическая проверка

Другой способ проверки неколлинеарности векторов — это использование аналитических методов. Мы можем представить векторы в виде координат и рассмотреть их алгебраические свойства. Если ранг матрицы, составленной из координат векторов, равен количеству векторов, то они неколлинеарны. Например, для двух векторов A(x1, y1) и B(x2, y2) мы можем составить матрицу и проверить ее ранг, чтобы убедиться в их неколлинеарности.

3. Использование скалярного произведения

Скалярное произведение двух векторов также может быть использовано для проверки их неколлинеарности. Если скалярное произведение равно нулю, то векторы ортогональны и следовательно, неколлинеарны. Например, для двух векторов AB и AC мы можем найти их скалярное произведение и проверить, равно ли оно нулю.

4. Использование векторного произведения

Векторное произведение двух векторов также может помочь в проверке неколлинеарности. Если векторное произведение равно нулю, то векторы коллинеарны. Таким образом, если векторное произведение двух векторов AB и AC равно нулю, то эти векторы лежат на одной прямой и следовательно, коллинеарны.

Вот некоторые способы проверки неколлинеарности векторов. Используйте их, чтобы решать геометрические задачи и лучше понимать пространственные отношения между векторами. Удачи в изучении геометрии!

Свойства неколлинеарных векторов

1. Линейная независимость

Одно из основных свойств неколлинеарных векторов — это их линейная независимость. Это означает, что ни один из этих векторов не может быть представлен как линейная комбинация других векторов. Другими словами, неколлинеарные векторы не могут быть выражены через друг друга с помощью умножения на скаляры.

2. Образование треугольника

Еще одно полезное свойство неколлинеарных векторов — это их способность образовывать треугольник. Если мы берем два неколлинеарных вектора и начинаем их наложение один на другой, то мы можем получить третий вектор, который является их суммой или разностью. Этот третий вектор будет вершиной треугольника, образованного первыми двумя векторами.

3. Ориентированный объем

4. Перпендикулярность

Неколлинеарные векторы также могут быть перпендикулярными друг к другу. Это означает, что они образуют прямой угол, то есть угол между ними равен 90 градусам. Перпендикулярные векторы могут быть использованы для решения задач, связанных с определением ортогональности фигур в геометрии.

Неколлинеарные векторы в геометрии 9 класс

Для того чтобы векторы были неколлинеарными, они должны удовлетворять следующему условию: они не должны лежать на одной прямой. Если векторы удовлетворяют этому условию, то их можно называть линейно независимыми.

Свойства неколлинеарных векторов:

1. Неколлинеарные векторы не могут быть пропорциональными. Если векторы пропорциональны, то они лежат на одной прямой и являются коллинеарными.
2. Неколлинеарные векторы можно складывать и вычитать. Сложение векторов выполняется таким образом, что получившийся вектор имеет длину, равную сумме длин слагаемых векторов, и направление, равное направлению первого вектора. Вычитание векторов выполняется аналогично сложению, но с изменением направления вычитаемого вектора.
3. Неколлинеарные векторы могут быть перемножены на число. Умножение вектора на число приводит к изменению его длины и/или направления.

Неколлинеарные векторы находят применение в геометрии, физике и других науках. Они позволяют описывать и анализировать сложные системы и явления, такие как движение тел, силы и траектории.