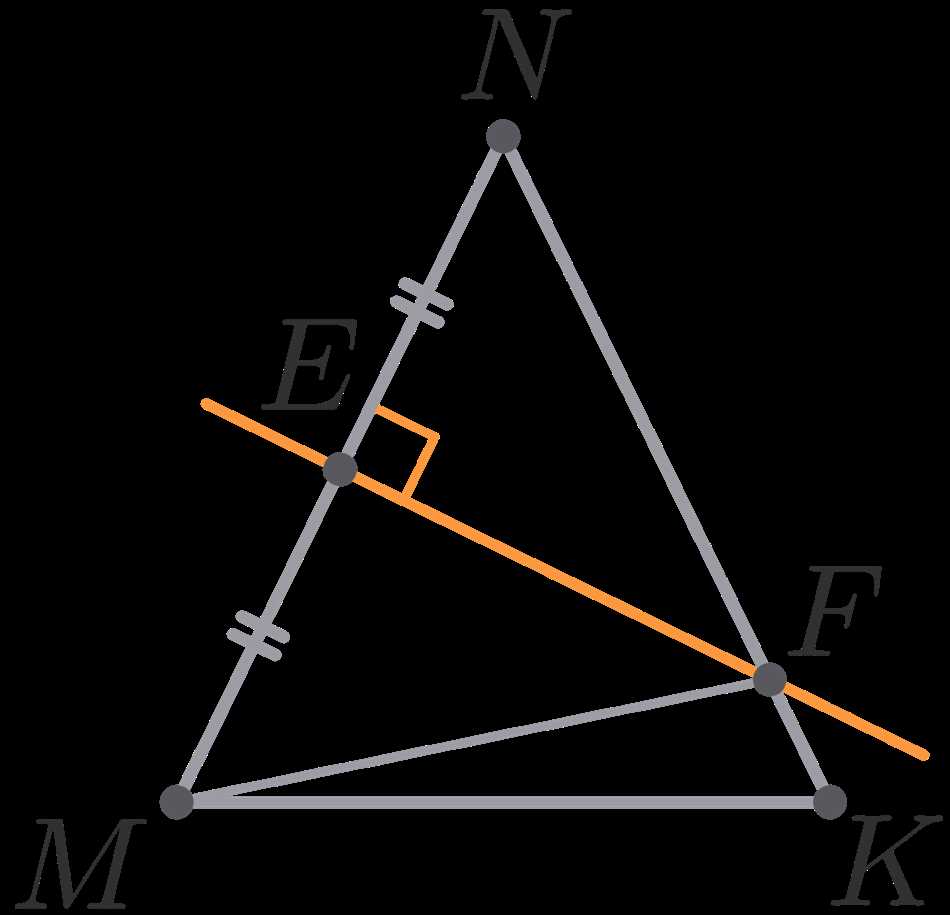
Серединные перпендикуляры являются важным понятием в геометрии. Они используются для определения точки пересечения двух прямых линий, проходящих через середины сторон геометрической фигуры и перпендикулярных им.
Учебник геометрии мог показаться сложным на первый взгляд, но на самом деле все не так уж и сложно. Если мы разобьем геометрию на более маленькие части и рассмотрим их отдельно, то все станет гораздо яснее.
Серединные перпендикуляры играют важную роль в построении и измерении геометрических фигур, а также в решении математических задач. Они помогают нам определить точку пересечения двух прямых линий и найти серединные точки геометрической фигуры.
Итак, серединные перпендикуляры представляют собой мощный инструмент в геометрии, который помогает нам лучше понять и анализировать формы и объекты в пространстве.
Определение серединных перпендикуляров
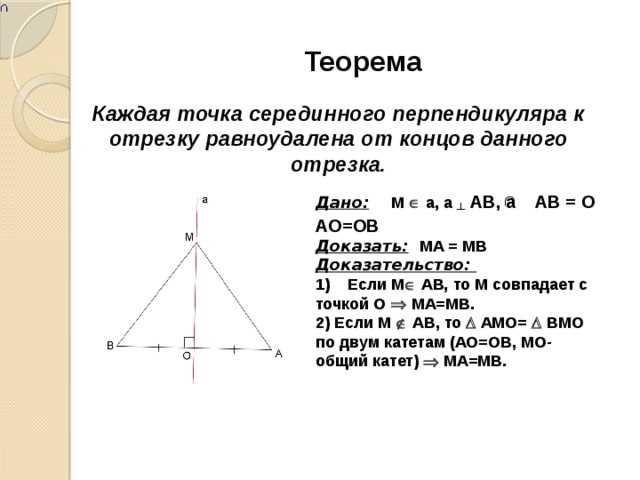
Знакомые ли вам понятия серединных перпендикуляров? Если нет, не волнуйтесь! Я расскажу вам все о них.
Серединные перпендикуляры являются прямыми линиями, которые пересекаются с другой линией (отрезком) в точке, находящейся точно посередине. То есть, если у вас есть отрезок AB, серединный перпендикуляр будет проходить через середину этого отрезка и быть перпендикулярным к нему.
Это понятие может показаться сложным, но на самом деле оно довольно простое. Как и всегда, ничто не может помешать нам разобраться в математике!
Давайте рассмотрим пример. Представьте, что у вас есть отрезок AB на бумаге. Чтобы найти серединный перпендикуляр, мы берем центр отрезка и, используя чертёжный инструмент, проводим линию, которая будет пересекать AB под прямым углом в точке M — середине отрезка. Эта линия и будет нашим серединным перпендикуляром.
Интересно, правда? Зачем вообще изучать такие перпендикуляры? Как и везде в математике, это понятие имеет много применений в реальном мире. Например, в архитектуре, серединные перпендикуляры помогают построить симметричные здания и структуры. Кроме того, они могут использоваться для измерения и выравнивания поверхностей, и даже для определения правильной положения объектов в геометрическом пространстве.
Так что, давайте не бойтесь математики и продолжим учиться! Знание серединных перпендикуляров откроет перед вами новые возможности и поможет вам лучше понимать окружающий мир.
Свойства серединных перпендикуляров
Во-первых, серединный перпендикуляр делит данный отрезок пополам. Это означает, что расстояние от конца отрезка до серединного перпендикуляра будет равно расстоянию от начала отрезка до серединного перпендикуляра. Если представить, что серединный перпендикуляр — это ось симметрии, то отрезок будет симметричным относительно этой оси.
Во-вторых, все серединные перпендикуляры для данного отрезка пересекаются в одной точке, называемой центром окружности описанной вокруг этого отрезка. Это означает, что если у тебя есть несколько серединных перпендикуляров для одного и того же отрезка, то все они должны пересечься в одной точке. И эта точка будет находиться на одинаковом расстоянии от концов отрезка.
Также стоит отметить, что серединные перпендикуляры, как правило, используются в геометрии для решения различных задач. Они помогают определить центр окружности, построить перпендикуляр к отрезку или найти точку пересечения двух прямых. Они просты в использовании и могут быть полезными инструментами в решении различных задач.
Применение серединных перпендикуляров
Одно из практических применений серединных перпендикуляров — это определение центра окружности. Мы можем использовать их, чтобы найти точку, которая находится на одинаковом расстоянии от всех точек окружности. Например, если у нас есть футбольный мяч и мы хотим найти его центр, мы можем провести серединные перпендикуляры к двум различным точкам на поверхности мяча, где они пересекутся — это и будет его центр.
Серединные перпендикуляры также используются в строительстве. Например, при постройке дома мы можем использовать их, чтобы найти середину стены и узнать, где находится центральная точка, чтобы разместить окно или дверь равномерно.
Еще одно применение серединных перпендикуляров связано с определением симметричных фигур. Если у нас есть фигура, мы можем провести серединные перпендикуляры к ее сторонам и найти точку пересечения, которая будет являться центром симметрии для этой фигуры.
Как видите, серединные перпендикуляры имеют много применений в нашей повседневной жизни. Они помогают нам находить центры, определять симметрию и строить равномерные конструкции. Знание о серединных перпендикулярах может быть полезным и в приятных, и в повседневных ситуациях!
Как строить серединные перпендикуляры?
Итак, как же нам построить серединный перпендикуляр?
- Возьми лист бумаги и нарисуй на нем прямую линию, которую мы будем делить пополам. Пусть эта линия будет AB.
- Теперь возьми компас и на концах линии AB отметь две одинаковые дуги, которые пересекаются. Пусть точки пересечения будут C и D.
- Соедини точки C и D прямой линией. Получился серединный перпендикуляр для отрезка AB!
Вот и все! Теперь у тебя есть серединный перпендикуляр, который делит отрезок AB на две равные части и проходит через его середину.
Очень полезно знать, как строить серединные перпендикуляры, так как они могут применяться в различных задачах. Например, если нам нужно найти точку равноудаленную от двух других точек, мы можем построить серединный перпендикуляр между этими точками и найти его пересечение с другой прямой.
Надеюсь, что объяснение было понятным и ты смог понять, как построить серединные перпендикуляры. Теперь ты можешь использовать этот метод в своих задачах и импонентировать своих друзей умением проводить такие математические построения!
Примеры использования серединных перпендикуляров

1. Построение центра окружности
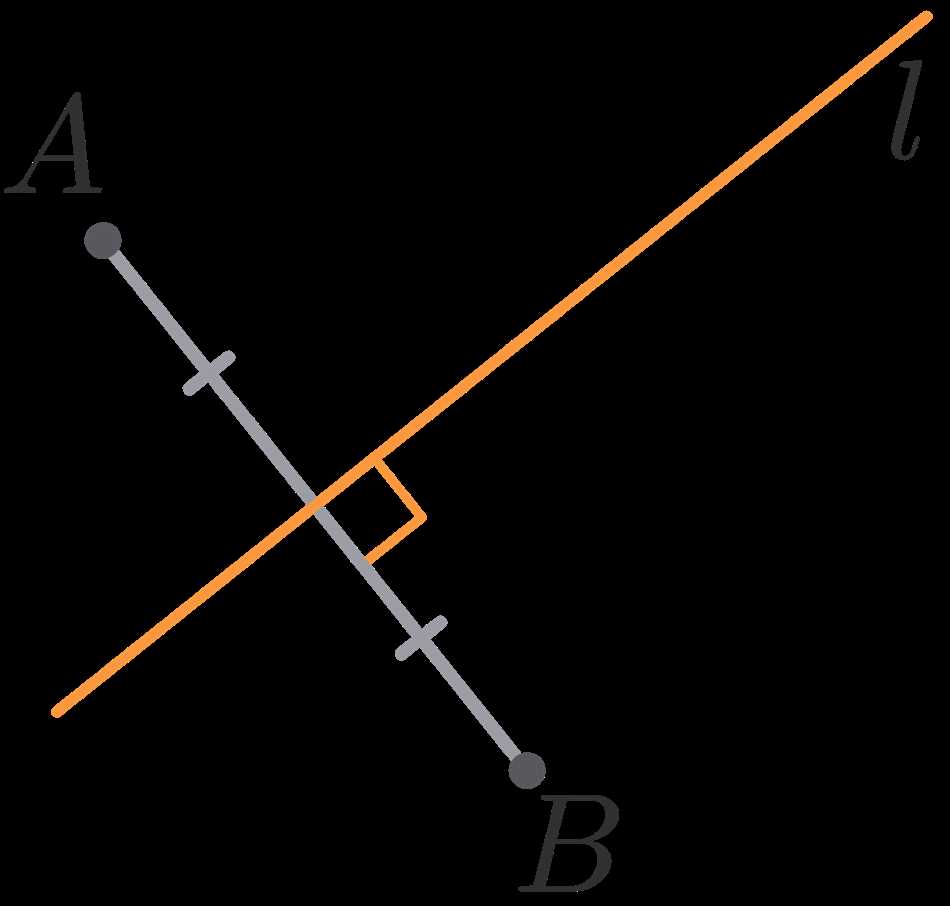
Серединные перпендикуляры могут использоваться для построения центра окружности. Для этого достаточно взять две точки на окружности, построить серединный перпендикуляр к отрезку, соединяющему эти точки, и найти точку его пересечения с окружностью. Эта точка будет центром окружности.
2. Разделение отрезка пополам
Еще один пример использования серединных перпендикуляров — разделение отрезка пополам. Если нужно разделить отрезок на две равные части, можно построить серединный перпендикуляр к этому отрезку и найти его точку пересечения с отрезком. Эта точка будет делить отрезок пополам.
3. Построение геометрических фигур
Серединные перпендикуляры также применяются при построении различных геометрических фигур. Например, для построения правильного шестиугольника можно взять серединный перпендикуляр к одной из его сторон, найти его точку пересечения с окружностью, описанной около шестиугольника, и соединить эту точку с вершинами шестиугольника. При этом получится правильный шестиугольник.
Таким образом, серединные перпендикуляры являются мощным инструментом, который находит свое применение в различных задачах геометрии и конструирования.




