Понятие коэффициента пропорциональности

Коэффициент пропорциональности — это понятие из математики, которое помогает понять, как связаны между собой два набора значений. Он используется для определения пропорциональной зависимости между двумя переменными. Когда мы говорим о пропорциональности, мы имеем в виду, что оба набора значений растут или убывают вместе. Такой относительный рост или убывание определяется коэффициентом пропорциональности, который часто обозначается символом «k». Он определяет, насколько единиц одной переменной соответствует единица другой переменной. Коэффициент пропорциональности может быть положительным или отрицательным числом.

Коэффициент пропорциональности: определение

Когда мы говорим о коэффициенте пропорциональности, мы имеем в виду число, которое устанавливает отношение между двумя переменными. В нашей жизни это может быть что угодно: пропорция между количеством времени и расстоянием, между весом и ростом, или даже между стоимостью и количеством продуктов в корзине.

Коэффициент пропорциональности является ключевым понятием в математике, так как с его помощью мы можем определить, как меняется одно значение при изменении другого. Когда коэффициент пропорциональности равен 1, это означает, что две переменные меняются в точности в одинаковой пропорции. И наоборот, когда коэффициент пропорциональности равен нулю, это означает, что две переменные не связаны.

Таким образом, коэффициент пропорциональности помогает нам понять, какие свойства вещей и явлений связаны друг с другом, и какая зависимость между ними существует.

Определение понятия «коэффициент пропорциональности»

Чтобы лучше понять этот концепт, давай рассмотрим пример. Допустим, у нас есть две переменные: x и y. Если x увеличивается в 2 раза, а y также увеличивается в 2 раза, то мы можем сказать, что между этими переменными существует пропорциональная связь. В этом случае коэффициент пропорциональности будет равен 1, так как оба значения увеличиваются одинаково.

Коэффициент пропорциональности выполняет роль множителя, который позволяет нам переходить от одной величины к другой. Если мы знаем значение одной величины и коэффициент пропорциональности, мы можем легко определить значение другой величины. Например, если у нас есть коэффициент пропорциональности 3 и мы знаем значение x равное 4, мы можем найти значение y, умножив x на коэффициент: 4 * 3 = 12.

Таким образом, коэффициент пропорциональности помогает нам понять и описать связь между двумя переменными, а также использовать эту связь для решения задач и предсказания значений.

Значение в математике

Давай рассмотрим пример: у нас есть уравнение 2x + 3y = 10. Если мы знаем значения x и y, мы можем найти значение выражения 2x + 3y. Например, если x = 2 и y = 1, то значение будет 2*2 + 3*1 = 4 + 3 = 7.

Значение также может относиться к функциям. Функция — это математическое правило, которое связывает одно значение (аргумент) с другим значением (значение функции). Например, функция f(x) = 2x + 3. Если мы знаем значение аргумента x, мы можем найти значение функции, подставив его вместо x. Например, если x = 4, то значение функции будет f(4) = 2*4 + 3 = 8 + 3 = 11.

Значение в математике помогает нам решать задачи, строить графики и делать прогнозы. Оно является основой для проведения различных операций и исследований. Поэтому понимание значения в математике чрезвычайно важно для развития наших навыков решения задач и аналитического мышления.

Как рассчитать коэффициент пропорциональности?

Для начала, представь себе, что у тебя есть две переменные — x и y. Они взаимосвязаны и зависят друг от друга. Для того чтобы рассчитать коэффициент пропорциональности, нужно взять одно значение x и соответствующее ему значение y. Чтобы найти коэффициент, необходимо поделить значение y на значение x. Полученное число и будет коэффициентом пропорциональности.

Например, у нас есть следующая пропорция: x = 3, y = 6. Чтобы рассчитать коэффициент пропорциональности, мы делим 6 на 3. Получаем значение 2. Просто, правда?

Коэффициент пропорциональности помогает нам понять, как одно значение зависит от другого. Если коэффициент равен 1, это означает, что значения полностью пропорциональны. Если коэффициент больше 1, то значения возрастают пропорционально друг другу. Если коэффициент меньше 1, значения убывают пропорционально.

Вот и все! Теперь ты знаешь, как рассчитать коэффициент пропорциональности. Надеюсь, этот материал был полезным для тебя. Удачи в изучении математики!

Практические примеры использования коэффициента пропорциональности

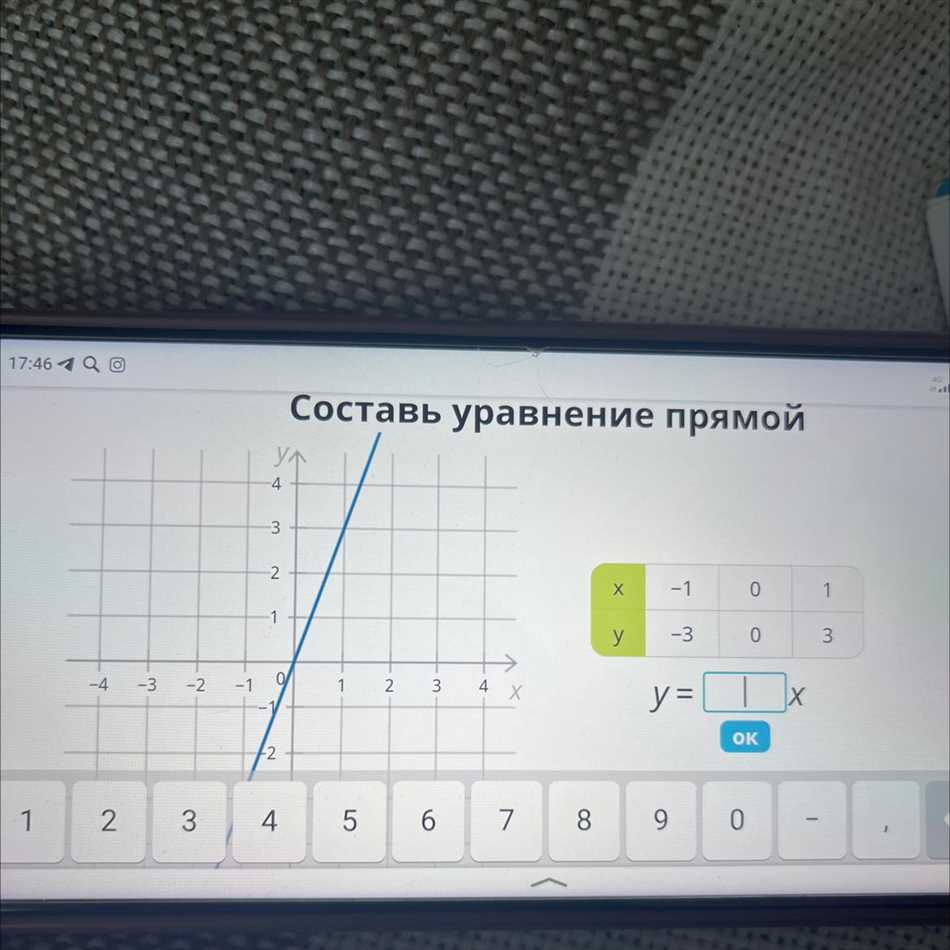
1. Тариф на перевозку грузов: Представим, что вы владелец грузовой компании, и вы хотите определить стоимость перевозки груза в зависимости от его веса. Здесь коэффициент пропорциональности будет связывать вес груза и стоимость перевозки. Чем больше вес груза, тем выше будет стоимость перевозки.

2. Пропорциональное увеличение заработной платы: Если вы работаете на почасовой оплате труда и ваш коэффициент пропорциональности составляет 15 долларов в час, то заработная плата будет пропорционально увеличиваться, если вы работаете больше часов. Например, если вы работаете 8 часов, ваша зарплата будет равна 120 долларам.

3. Соотношение между временем и расстоянием: Коэффициент пропорциональности также можно использовать для определения соотношения между временем и расстоянием. Например, если вы знаете, что коэффициент пропорциональности между временем и расстоянием равен 50 км/ч, то вы можете вычислить, сколько времени потребуется, чтобы пройти определенное расстояние. Если расстояние равно 100 километрам, то время, необходимое для его преодоления, будет равно 2 часам.

Вот некоторые практические примеры использования коэффициента пропорциональности. Он может быть полезен для решения различных задач, связанных с пропорциональными отношениями между данными. У вас есть еще какие-либо примеры, где вы использовали коэффициент пропорциональности?

Зависимость между переменными

Один из способов изучения этих изменений — это использование коэффициента пропорциональности. Этот коэффициент показывает связь между двумя переменными. Когда одна переменная увеличивается, а другая уменьшается, мы можем использовать коэффициент пропорциональности, чтобы выразить эту связь числом.

Коэффициент пропорциональности может быть положительным или отрицательным числом. Если коэффициент равен положительному числу, это означает, что переменные меняются в одном направлении. Например, если коэффициент равен 2, это означает, что с увеличением одной переменной в 2 раза, другая переменная тоже увеличивается в 2 раза.

С другой стороны, если коэффициент равен отрицательному числу, это означает, что переменные меняются в противоположных направлениях. Например, если коэффициент равен -0,5, то с увеличением одной переменной в 2 раза, другая переменная уменьшится в 0,5 раза.

Итак, зависимость между переменными — это прекрасное явление, которое помогает нам понять, как все в нашем мире взаимосвязано. Использование коэффициента пропорциональности поможет нам лучше понять эту связь и использовать ее в нашей повседневной жизни. А ты когда-нибудь задумывался о зависимости между переменными?