Понятие конгруэнтных треугольников и их особенности

Когда мы говорим о треугольниках, мы часто сталкиваемся с понятием «конгруэнтные треугольники». Но что это значит?

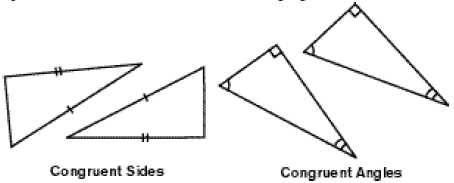
Конгруэнтные треугольники — это треугольники, которые имеют одинаковые размеры и форму. Каждая сторона и угол в одном треугольнике соответствует стороне и углу в другом. Но важно помнить, что они могут быть развёрнуты или повёрнуты в другом положении.

Понимание конгруэнтных треугольников очень полезно в геометрии и в реальной жизни. Используя эти концепции, мы можем изучать структуру и форму различных объектов, состоящих из треугольников, и решать задачи, связанные с построением и сравнением треугольников.

Определение конгруэнтных треугольников

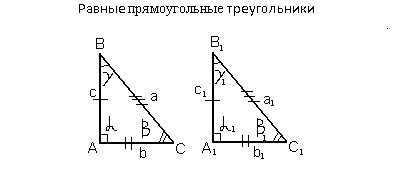
Углы и стороны треугольников должны быть точно одинаковыми, чтобы они были конгруэнтными. Например, треугольник ABC и треугольник DEF могут быть конгруэнтными, если сторона AB равна стороне DE, сторона BC равна стороне EF и сторона AC равна стороне DF. Кроме того, угол A должен быть равен углу D, угол B должен быть равен углу E и угол C должен быть равен углу F.

Конгруэнтные треугольники могут быть полезны для решения задач в геометрии. Например, если ты знаешь, что два треугольника конгруэнтны, то ты можешь использовать это знание для нахождения недостающих сторон и углов. Конгруэнтность треугольников — это важное понятие в геометрии, которое помогает нам понимать и анализировать формы и фигуры.

Что значит «конгруэнтные»?

Когда два треугольника являются конгруэнтными, это означает, что все их стороны и углы равны друг другу. Это как две копии одного и того же треугольника, которые можно полностью наложить друг на друга без каких-либо пропорциональных изменений.

Мы можем определить конгруэнтность треугольников, сравнивая их стороны и углы. Если все стороны одного треугольника равны соответствующим сторонам другого, и все углы также равны, то мы можем сказать, что эти треугольники конгруэнтны. Однако, порой достаточно знать только одну сторону и два угла треугольника, чтобы сказать о его конгруэнтности с другим.

• Сторона-сторона-сторона (ССС) — все три стороны одного треугольника равны соответствующим сторонам другого треугольника.
• Угол-сторона-угол (УСУ) — два угла и между ними лежащая сторона одного треугольника равны соответствующим углам и между ними лежащей стороне другого треугольника.
• Сторона-угол-сторона (СУС) — две стороны и между ними лежащий угол одного треугольника равны соответствующим сторонам и между ними лежащему углу другого треугольника.

Заключая, когда мы говорим о треугольниках или других фигурах, которые являются конгруэнтными, мы имеем в виду, что они имеют одинаковую форму и размеры, и все их стороны и углы равны друг другу. Это понятие играет важную роль в геометрии и имеет множество практических применений. Надеюсь, тебе интересно было узнать об этом!

Свойства конгруэнтных треугольников

Мы знаем, что конгруэнтные треугольники имеют равные стороны и углы. Но какие еще свойства они имеют?

• Конгруэнтные треугольники имеют одинаковую форму и размер.
• Они имеют одинаковую площадь.
• Углы между соответствующими сторонами в конгруэнтных треугольниках равны.
• Сумма всех углов в треугольнике всегда равна 180°, поэтому если два треугольника конгруэнтны, то их все углы равны.
• Главные свойства конгруэнтных треугольников — это равенство сторон и равенство углов между ними.

Какие же применения могут быть у конгруэнтных треугольников?

Применение

• Используя свойства конгруэнтных треугольников, мы можем доказать равенство или подобие других геометрических фигур.
• Конгруэнтные треугольники могут использоваться для решения задач на построение фигур.
• Они также помогают нам в доказательстве теорем и различных геометрических утверждений.

Интересно, правда? Теперь вы знаете всю суть конгруэнтных треугольников и их свойства. Получается, геометрия может быть не только интересной, но и полезной!

Равенство соответствующих углов

Равенство соответствующих углов означает, что углы двух конгруэнтных треугольников одинаковы, или, другими словами, соответствующие углы в обоих треугольниках имеют одни и те же меры. Это означает, что если мы имеем два конгруэнтных треугольника, и угол A в первом треугольнике соответствует углу A’ во втором треугольнике, то мера этих углов будет одинаковой.

Понимание равенства соответствующих углов поможет вам лучше понять свойства конгруэнтных треугольников и использовать их для решения геометрических задач. Так что давайте изучим это свойство внимательнее и посмотрим, как мы можем его применить!

Равенство соответствующих сторон

Великолепно! Мы еще немного приближаемся к разгадке тайны конгруэнтных треугольников. Теперь давайте поговорим о равенстве соответствующих сторон этих треугольников.

Итак, что вообще значит равенство соответствующих сторон? Все очень просто. Если у нас есть два конгруэнтных треугольника, то каждая сторона одного треугольника будет равна соответствующей стороне другого треугольника.

Можно сказать, что эти треугольники весьма понимаются друг с другом и делают все возможное, чтобы их стороны не отличались друг от друга. Ну не так ли?

Так что если у нас есть, скажем, два треугольника с равными сторонами AB и CD, то это означает, что AB=CD. И это применимо ко всем соответствующим сторонам этих треугольников. Впечатляюще, верно?

Итак, мы обсудили понятие конгруэнтности треугольников, рассмотрели критерии и условия их конгруэнтности, исследовали некоторые свойства и, наконец, поговорили о равенстве соответствующих сторон. А что мы будем обсуждать дальше? Давайте сделаем перерыв и придумаем интересный вопрос для следующего раздела!

Способы доказательства конгруэнтности треугольников

Когда мы говорим о конгруэнтности треугольников, это означает, что у них все стороны и углы равны друг другу. Но как мы можем доказать, что два треугольника конгруэнтны? Существует несколько способов, которые нам в этом помогают.

Второй способ — использовать свойства равных треугольников. Если мы знаем, что два треугольника имеют одну сторону и два прилежащих угла равными, то мы можем утверждать, что они конгруэнтны. Например, если у двух треугольников сторона A, прилежащие углы α и β равны, то мы можем сказать, что треугольники конгруэнтны.

• Первый способ: равенство сторон и углов
• Второй способ: использовать свойства равных треугольников
• Третий способ: использовать свойства равных треугольников

По трем сторонам

Такой подход основан на основной теореме о существовании равных треугольников. Любые две треугольника с равными сторонами и равными углами считаются конгруэнтными. Используя этот подход, мы можем узнать, конгруэнтны ли треугольники, просто измерив их стороны.

Однако, не все треугольники, у которых все три стороны равны, являются конгруэнтными. Чтобы убедиться, что треугольники действительно конгруэнтны, мы должны убедиться, что у них также равны соответствующие углы. Это можно сделать, используя другие методы, такие как сравнение углов или использование других известных свойств треугольников.

Интересно, не правда ли? Можете ли вы найти два треугольника, у которых все три стороны равны, но они все равно не являются конгруэнтными? Подумайте над этим и делитесь своими мыслями!