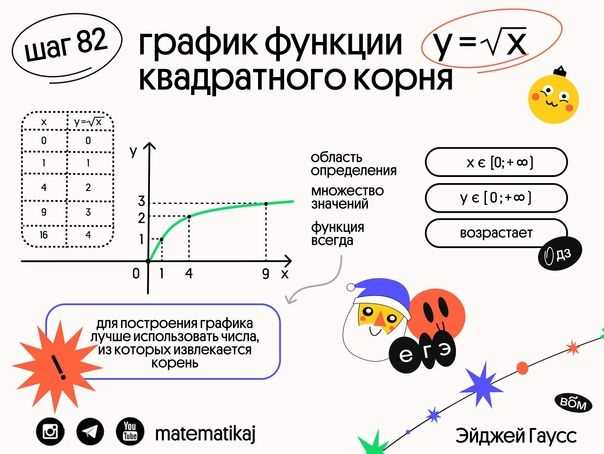
Корень функции — это значение аргумента, при котором значение самой функции равно нулю. Если представить, что график функции — это дорожка, то корень функции — это точка, где функция «пересекает» ось абсцисс, то есть совпадает с нулевым значением по вертикальной оси.
Корень функции обычно ищется с помощью различных математических методов, таких как метод деления отрезка пополам или метод Ньютона. Найдя корень функции, мы можем определить значение аргумента, при котором функция будет равна нулю, что может быть полезно при решении уравнений или определении точек пересечения графиков функций.
Корень функции помогает нам более глубоко понять и исследовать ее свойства и поведение на протяжении всего диапазона значений аргумента.
Формальное определение корня функции
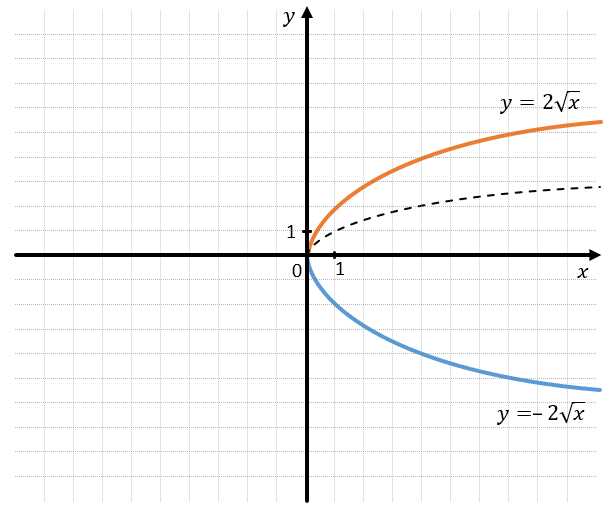
Формально, корень функции f(x) — это такое значение x, при котором f(x) равно нулю. Другими словами, это точка на графике функции, где она пересекает ось x. Если вы еще ощущаете запутанность, не беспокойтесь, это нормально. Математика иногда может быть сложной, но сам процесс поиска корня функции — это интересное путешествие по миру чисел и символов.
Интересно, правда? Но постойте! Зачем нам все это? В реальном мире мы используем корень функции для различных целей — от решения уравнений до определения места, где две функции пересекаются. И знание формального определения корня функции поможет нам лучше понять и использовать его в повседневной жизни.
Графическое представление корня функции
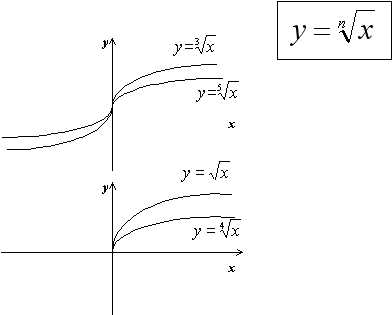
Когда мы говорим о графическом представлении корня функции, мы могли бы сказать, что это довольно интересная тема. Ну, или можно сказать, что это довольно важная тема. В любом случае, это тема, о которой мы с вами сейчас поговорим.
Так что же такое графическое представление корня функции? Для начала давайте разберемся, что такое функция. Функция — это просто математическое выражение, которое связывает одни значения с другими. А корень функции — это значение аргумента, при котором функция равна нулю. То есть, если мы найдем такое значение аргумента, при котором функция обращается в ноль, то мы нашли корень функции. И графическое представление корня функции позволяет нам визуализировать этот корень на графике.
Чтобы нарисовать график функции и найти её корни, мы используем координатную плоскость. Мы рисуем оси x и y и отмечаем на них точки, которые соответствуют значениям функции при разных значениях аргумента. Когда наша функция обращается в ноль, это означает, что она пересекает ось x. И эта точка пересечения будет являться корнем функции. Мы можем найти эту точку на графике и прочитать значение аргумента, которое соответствует корню функции.
Таким образом, графическое представление корня функции позволяет нам наглядно увидеть место, где функция обращается в ноль и найти значение аргумента, для которого это происходит. Это очень полезное инструмент в изучении функций и их свойств. Так что давайте не бойтесь графиков и не стесняйтесь исследовать функции на их корни!
Применение корня функции в реальной жизни
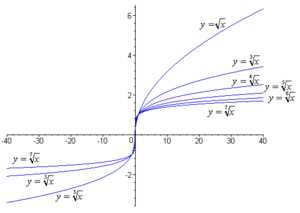
Прости, что вмешиваюсь в твою жизнь, но ты когда-нибудь задумывался о том, где мы можем применить корень функции в нашей реальной жизни? Нет? Ну что ж, позволь мне показать тебе несколько интересных примеров, где мы можем использовать эту математическую концепцию.
Давай сначала поговорим о финансах. Мы все инвестируем деньги, верно? И когда мы хотим узнать доходность наших инвестиций или вычислить, какую сумму нужно инвестировать, чтобы достичь определенной цели, мы можем использовать корень функции. Это позволит нам найти решение наших финансовых проблем и достичь желаемого успеха.
Теперь давай поговорим о нашем здоровье. Когда мы посещаем врача, его задача — определить, сколько лекарства нам нужно принять, чтобы достичь желаемого эффекта. И так, врачи часто используют корень функции для расчета необходимой дозировки. Это позволяет нам получить правильное лечение и быстрее вернуться к здоровой жизни.
Ну что, я привлек твое внимание? Преимущества использования корня функции в нашей повседневной жизни очевидны. От финансовых решений до здоровья, мы можем положиться на эту математическую концепцию, чтобы найти оптимальное решение и достичь желаемого результата.
Заключение
Мы выяснили, что корни функции могут быть одним или несколькими и могут быть найдены с помощью различных методов, таких как графический, аналитический и численный. Некоторые из этих методов требуют использования специальных формул и алгоритмов, в то время как другие могут быть реализованы с помощью программного обеспечения.
Использование корня функции в решении уравнений может быть очень полезным в научных и инженерных расчетах, а также в различных приложениях, где требуется найти определенные значения переменных для достижения определенной цели.
В целом, знание о корне функции позволяет нам глубже понять поведение функций и решать уравнения эффективным образом. Оно является фундаментальным инструментом в математике и имеет широкое применение в различных областях знаний.
Вопрос-ответ:
Как можно использовать корень функции для решения уравнений?
Корень функции может использоваться для решения уравнений путем приравнивания функции к нулю и нахождения значений аргумента, при которых функция равна нулю.
Как найти корень функции?
Корень функции можно найти путем решения уравнения f(x) = 0. Методы решения могут включать численные методы, графический метод, и аналитический метод, в зависимости от сложности функции.
Как найти корни квадратного уравнения с использованием корня функции?
Для нахождения корней квадратного уравнения можно использовать формулу корней: x = (-b ± √(b^2 — 4ac)) / 2a, где a, b и c — коэффициенты уравнения.