Обыкновенная дробь — это дробное число, которое состоит из двух чисел: числителя и знаменателя. В 5 классе начинают изучать эту тему, чтобы научиться работать с дробями. Знание обыкновенных дробей играет важную роль в решении различных математических задач. Они помогают сравнивать, складывать, вычитать и умножать дроби. Понимание обыкновенных дробей позволяет нам разделять предметы и идеи на части, а также применять их в повседневной жизни. В этой теме мы узнаем, как сократить дроби, находить их эквивалентные значения и выполнять различные операции с ними. Погрузимся в мир обыкновенных дробей и начнем исследование!
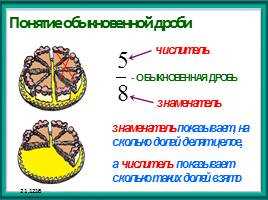
Определение обыкновенной дроби
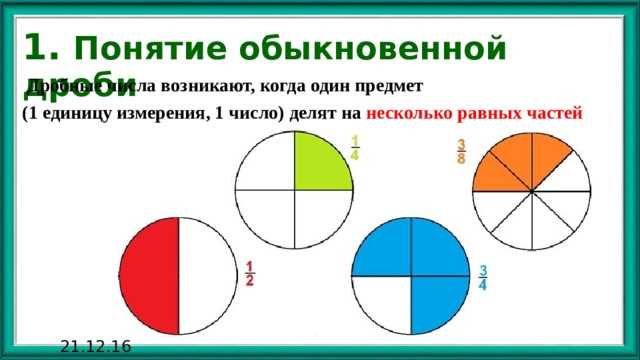
Числитель обозначает количество частей целого числа, которые мы рассматриваем, а знаменатель показывает на сколько частей было разделено целое число. Например, если мы разбили пирог на 8 частей и взяли 3 из них, мы можем записать это в виде обыкновенной дроби 3/8.
Обыкновенная дробь — это нецелое число и может быть представлена в виде конечной или бесконечной десятичной дроби. Конечная десятичная дробь имеет ограниченное число десятичных знаков, например 0,5. Бесконечная десятичная дробь не имеет конечного числа десятичных знаков и повторяющихся групп цифр, например 0,3333…
Обыкновенные дроби могут использоваться для сравнения и упрощения нецелых чисел. Они также часто используются в задачах о долях, долях от суммы и других задачах, связанных с разделением целого на части.
Теперь, когда вы знаете определение обыкновенной дроби, вы сможете легче работать с ними и решать математические проблемы, которые они включают в свои задания. Учитесь, практикуйтесь и не бойтесь задавать вопросы, если вы сталкиваетесь с трудностями. Математика может быть увлекательной и полезной наукой!
Общая информация
Обыкновенная дробь — это дробь, у которой числитель меньше знаменателя. Например, 3/5. Числитель может принимать любое целое число, кроме нуля, а знаменатель — любое целое число, кроме нуля.
Использование обыкновенных дробей в нашей жизни очень распространено. Мы можем встретить их во многих ситуациях. Например, когда мы готовим пирог и добавляем 1/2 стакана сахара. Или, когда мы делим пиццу на 4 равные части и берем одну четверть пиццы. Вот такие простые примеры показывают, что знание обыкновенных дробей очень полезно в повседневной жизни.
Также, обыкновенные дроби широко применяются в науке и технике. Они помогают нам считать и измерять различные величины. Например, при расчетах для строительных работ, дроби могут использоваться для указания размеров и пропорций.
Итак, обыкновенная дробь — это важная и полезная математическая концепция. Знание обыкновенных дробей поможет нам разбираться во многих ситуациях и делать правильные математические вычисления. Не стесняйся задавать вопросы, если что-то непонятно. Учение — это процесс и все мы вместе движемся вперед!
Числитель и знаменатель
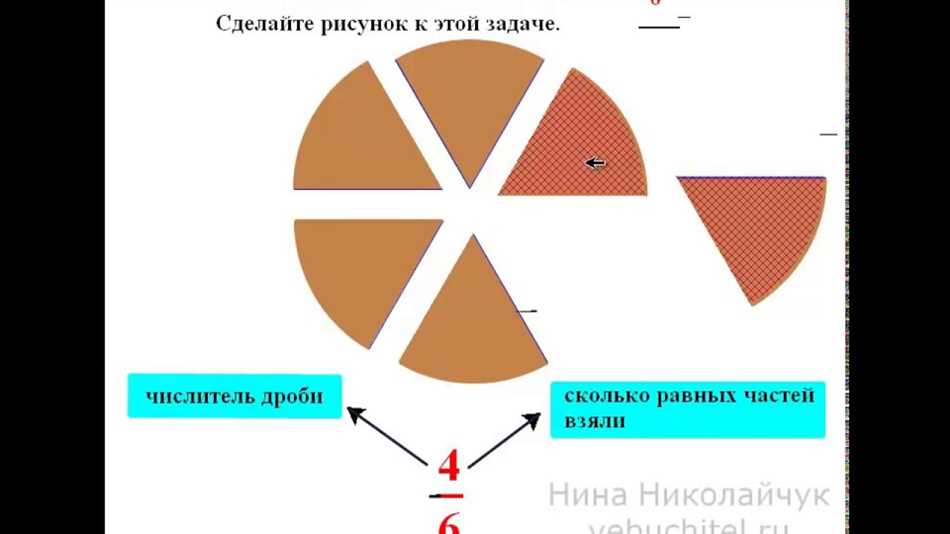
Числитель показывает, сколько частей целого мы имеем, а знаменатель показывает, на сколько равных частей мы делим целое. Например, если у нас есть дробь 3/4, то числитель равен 3, что означает, что мы имеем 3 части из целого, а знаменатель равен 4, что означает, что мы делим целое на 4 равные части.
Числитель и знаменатель образуют пару, которая определяет значение дроби. Если изменить либо числитель, либо знаменатель, то значение дроби также изменится. Например, если у нас есть дробь 2/3 и мы увеличим числитель до 4, то значение дроби станет равным 4/3. В то же время, если мы увеличим знаменатель до 6, то значение дроби станет равным 2/6.
Числитель и знаменатель образуют пару, в которой они взаимосвязаны и влияют друг на друга. Они помогают нам понять, насколько целое число делится на равные части и какое количество частей целого мы имеем.
Сокращение дробей
Давайте разберемся, как сокращать дроби на примере. Представьте, у нас есть обыкновенная дробь 6/8. Для того чтобы ее сократить, мы должны найти наибольший общий делитель числителя и знаменателя. В данном случае, наибольший общий делитель чисел 6 и 8 равен 2. Теперь делим числитель и знаменатель на этот наибольший общий делитель:
6 ÷ 2 = 3
8 ÷ 2 = 4
Итак, дробь 6/8 после сокращения равна 3/4.
Теперь давайте рассмотрим другой пример. Предположим, у нас есть дробь 12/16. Находим наибольший общий делитель чисел 12 и 16, и получаем, что он равен 4. Делим числитель и знаменатель на 4:
12 ÷ 4 = 3
16 ÷ 4 = 4
Таким образом, после сокращения дробь 12/16 превращается в 3/4.
Уже видно, что сокращение дробей помогает нам в работе с числами. Этот навык особенно полезен, когда мы работаем с большими числами, где общие делители не всегда очевидны. Практика и опыт помогут вам научиться находить наибольший общий делитель быстро и эффективно.
Теперь, когда вы знаете, как сокращать дроби, попробуйте сами решить задачу. Например, как сократить дробь 15/20? Найдите наибольший общий делитель и поделите числитель и знаменатель на него.
Хорошая работа! Вы научились сокращать дроби. Продолжайте практиковаться и решать задачи, чтобы стать настоящим мастером сокращения дробей!
Простые и составные дроби
Простые дроби
Простая дробь — это дробь, которая не может быть упрощена или разложена на меньшие доли. Она представляет собой отношение двух натуральных чисел, где числитель и знаменатель не имеют общих делителей, кроме единицы. Например, дроби 2/3, 5/7 и 11/13 являются простыми дробями.
Простые дроби могут быть представлены в виде числитель/знаменатель или десятичного значения. Но кроме того, они могут быть представлены и в виде процента или изменение из одной формы к другой.
Простые дроби применяются во многих сферах жизни. В мире кулинарии, например, они используются для измерения ингредиентов при приготовлении блюд. Также простые дроби могут быть полезны для оценки вероятности, расчета площади и объема, а также для решения математических задач.
Составные дроби
Составная дробь — это дробь, которая может быть разложена на сумму или разность двух или более простых дробей. Она состоит из двух или более частей, которые могут быть представлены в виде отдельных дробей. Например, дробь 3/4 может быть разложена на сумму двух простых дробей: 1/2 и 1/4.
Составные дроби часто используются для решения сложных задач, где требуется провести дополнительные вычисления и упрощение. Они могут быть полезными при решении уравнений и проблем, связанных с финансами или наукоемкими исследованиями.
Обратите внимание на то, что простые дроби являются составной частью составных дробей. Они играют важную роль в изучении и понимании обыкновенных дробей. Поэтому, чтобы быть успешным в решении задач, связанных с дробями, важно хорошо понять разницу между простыми и составными дробями.
Десятичная запись обыкновенной дроби
Для того, чтобы перевести обыкновенную дробь в десятичную запись, нужно разделить числитель на знаменатель. Например, если у нас есть дробь 3/4, то мы делим 3 на 4:
3 ÷ 4 = 0.75
Таким образом, десятичная запись дроби 3/4 будет равна 0.75. Мы можем сказать, что 0.75 — это эквивалент дроби 3/4 в десятичной форме.
При работе с обыкновенными дробями в школе, мы часто сталкиваемся с примерами, где знаменатель дроби является степенью числа 10, таким как 10, 100 или 1000. В таких случаях десятичная запись обыкновенной дроби будет содержать конечное количество разрядов после запятой.
Например, для дроби 1/10, мы знаем, что знаменатель равен 10. Поэтому, чтобы перевести дробь 1/10 в десятичную форму, мы делим 1 на 10:
1 ÷ 10 = 0.1
Таким образом, десятичная запись дроби 1/10 будет равна 0.1. Здесь у нас только один знак после запятой.
Итак, десятичная запись обыкновенной дроби представляет ее в виде числа с плавающей запятой. Она показывает соотношение между числителем и знаменателем дроби, позволяя нам легко сравнивать и работать с ней в математических операциях.
Обыкновенная дробь
Например, в дроби 3/5, числитель 3 указывает на то, что имеется 3 равные части, а знаменатель 5 показывает, что все целое число было разделено на 5 равных частей.
Когда мы говорим о дробных числах, они могут быть представлены в нескольких форматах. Например, дробь 3/5 можно представить в виде десятичной дроби 0,6 или в процентном виде 60%.
Дроби используются для представления и группировки частей целого числа, также как и для описания отношений и долей в математических задачах.
Обыкновенные дроби активно используются в различных областях, таких как финансы, строительство, кулинария и многих других, где необходимо работать с дробными значениями.