Давайте разберемся, что значит быть самодвойственной функцией. Самодвойственная функция — это такая функция, которая при отражении относительно своей прямой уравнивается с ее отражением. Другими словами, самодвойственная функция остается неизменной при инвертировании своих битов. Важно понимать, что самодвойственные функции различным образом используются в информационных технологиях, логике, электротехнике и теории автоматов. Они широко применяются в цифровых системах и схемах, таких как компьютеры, телефоны и другие устройства.
Самодвойственные функции имеют ряд интересных свойств и особенностей. Знание о них помогает в создании более эффективных и надежных систем. Теперь, когда вы понимаете, что такое самодвойственная функция, можно исследовать их дальше и изучить, как они применяются в различных областях техники и науки.
- Самодвойственная функция: определение и свойства
- Определение самодвойственной функции
- Свойства самодвойственной функции
- Примеры самодвойственных функций
- Пример 1
- Пример 2
- Роль самодвойственных функций в криптографии
- Вопрос-ответ:
- Какие функции называются самодвойственными в криптографии?
- Какую роль играют самодвойственные функции в криптографии?
- Какие примеры самодвойственных функций можно привести?
Самодвойственная функция: определение и свойства

Такое свойство делает самодвойственные функции особенно интересными и полезными. Они играют важную роль в различных математических и логических теориях, а также в разработке компьютерных алгоритмов и схем.
Одно из ключевых свойств самодвойственной функции – симметрия. Обратное преобразование битов входной последовательности превращает самодвойственную функцию в самодвойственную, и наоборот. Это позволяет упростить анализ и использование таких функций.
Важно отметить, что самодвойственные функции встречаются в разных областях науки и технологии, например, в теории графов, криптографии, коммутационных схемах, и даже в некоторых вопросах квантовой физики.
Таким образом, самодвойственные функции представляют собой уникальный класс функций, сочетающий в себе особые свойства, которые находят широкое применение и имеют значительное значение в различных областях науки и технологии.
Определение самодвойственной функции

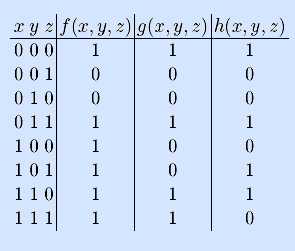
Другими словами, если мы поменяем все единицы на ноли и все ноли на единицы в таблице истинности самодвойственной функции, то получим ту же самую таблицу истинности, которая была изначально.
Примером самодвойственной функции запись логики является операция исключающего «или», обозначаемая как XOR. Если мы построим таблицу истинности для XOR, то увидим, что если поменять местами единицы и ноли, то результаты тоже перевернутся. Вот пример:
| A | B | XOR(A,B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Самодвойственные функции также играют важную роль в криптографии и комбинаторике. Они имеют множество приложений в различных областях, и их изучение помогает лучше понять основы логики и алгоритмов.
Свойства самодвойственной функции

- Отражение: Когда мы меняем переменные функции на их отрицания (0 на 1 и 1 на 0), самодвойственная функция отражается относительно точки (0, 0). Это означает, что если мы нарисуем график самодвойственной функции, а затем отразим его относительно точки (0, 0), получим такой же график.
- Формула Де Моргана: Самодвойственные функции обладают особым свойством, известным как формула Де Моргана. Она гласит, что если мы инвертируем каждую переменную функции и заменим логическое И на логическое ИЛИ, а логическое ИЛИ на логическое И, то получим ту же самую функцию, но с инвертированными переменными.
Итак, самодвойственные функции обладают уникальными свойствами, которые делают их особенными. Они позволяют нам использовать простые трюки и преобразования для анализа и упрощения логических выражений. Использование этих свойств позволяет нам сэкономить время и усилия при работе с самодвойственными функциями.
Примеры самодвойственных функций
Примером самодвойственной функции может служить функция импликации, обозначаемая символом «->». Когда мы подставляем в импликацию данное высказывание и его отрицание, результат всегда будет истинным. Например, если высказывание «Если сегодня идет дождь, значит улица мокрая» и его отрицание «Если сегодня не идет дождь, значит улица не мокрая», то оба высказывания будут верными.
Другим примером самодвойственной функции является конъюнкция (логическое «и»). Если обозначить ее символом «&», то при подставлении данного высказывания и его отрицания результат всегда будет ложным. Например, если высказывание «Солнце светит и птицы поют» и его отрицание «Солнце не светит и птицы не поют», то оба высказывания будут ложными.
Другие примеры самодвойственных функций включают исключающее ИЛИ (XOR), отрицание (НЕ) и эквиваленцию (равенство).
Самодвойственные функции имеют важное значение в математике и логике, поскольку позволяют упрощать выражения и делать более эффективные логические операции.
Пример 1
Тебе уже когда-нибудь доводилось слышать о самодвойственной функции? Если нет, то сегодня я расскажу тебе об одном интересном примере.
Допустим, у нас есть функция f(x), которая определена на множестве {0, 1}. Если мы рассмотрим таблицу истинности этой функции, то обнаружим, что она приобретает такие значения:
| x | f(x) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Интересно, не правда ли? Мы можем заметить, что значение функции меняется в зависимости от значения аргумента. Если x = 0, то f(x) = 1, а если x = 1, то f(x) = 0. Такая функция называется самодвойственной.
Но что это значит? Самодвойственная функция обладает свойством, при котором результат ее применения к своему собственному значенияю меняется. Проще говоря, функция противоположна самой себе. В нашем примере, если мы применим функцию f к ее собственным значениям (0 или 1), результат всегда будет противоположным.
Это лишь один пример самодвойственной функции, но их существует гораздо больше. Каждая из них интересна своей особенностью и может иметь различные применения в разных областях, таких, как математика, логика, информатика и т.д.
Теперь, когда мы знаем, что такое самодвойственная функция и как она работает, можно оценить ее важность и использование в различных задачах. Возможно, ты встретишь еще одну самодвойственную функцию в будущем и сможешь оценить ее применение.
Пример 2
Представьте, что вы уже знакомы с самодвойственными функциями и хотите найти конкретный пример. Возьмем функцию побитового исключающего ИЛИ (XOR) в языке программирования C++.
Эта функция применяет операцию исключающего ИЛИ к двум операндам и возвращает значение, равное true, если один из операндов истинный, и false, если оба операнда истинные или оба ложные. Вот пример кода:
#include <iostream>
using namespace std;
bool xorFunc(bool a, bool b) {
return a xor b;
}
int main() {
bool x = true;
bool y = false;
bool result = xorFunc(x, y);
if (result) {
cout << "Один из операндов истинный!" << endl;
} else {
cout << "Оба операнда ложные или истинные!" << endl;
}
return 0;
}
Таким образом, функция побитового исключающего ИЛИ в языке C++ является примером самодвойственной функции, потому что ее результат зависит только от одного операнда исключительного ИЛИ и того, является ли этот операнд истинным или ложным. Это интересный пример, который позволяет лучше понять понятие самодвойственной функции и ее применение в программировании.
Роль самодвойственных функций в криптографии
Самодвойственная функция (или автоморфизм) - это функция, которая возвращает свое собственное дуальное отображение при инверсии. Другими словами, операция инверсии не меняет результат исходной функции. Из этого свойства следует множество важных характеристик самодвойственных функций, таких как их невозможность представления в виде полиномиальной формы и высокая устойчивость к атакам, основанным на линейной алгебре.
В криптографии самодвойственные функции используются для создания сильных и надежных схем шифрования. Их особенности и свойства позволяют создавать криптографические алгоритмы, устойчивые к различным методам взлома, включая линейные и дифференциальные атаки. Они также широко применяются в области аутентификации, контроля целостности данных и других аспектов безопасности информации.
Использование самодвойственных функций в криптографии обеспечивает высокий уровень безопасности и защиты данных. Они служат основой для разработки прочных алгоритмов шифрования, которые становятся надежным инструментом в защите информации от несанкционированного доступа. Благодаря своим особенностям и высокой надежности, самодвойственные функции продолжают активно применяться в современной криптографии и играют важную роль в обеспечении безопасности в информационных системах и сетях.
Вопрос-ответ:
Какие функции называются самодвойственными в криптографии?
Самодвойственные функции - это такие логические функции, удовлетворяющие условию: при инвертировании всех входных и выходных битов должны получаться те же значения выходных битов.
Какую роль играют самодвойственные функции в криптографии?
Самодвойственные функции имеют важное значение в криптографии, так как они могут использоваться в построении криптографических алгоритмов, таких как блочные шифры, хеш-функции, генераторы псевдослучайных чисел и др. Они позволяют обеспечить свойство неуязвимости к атакам методами линейного криптоанализа и многочленов Буле.
Какие примеры самодвойственных функций можно привести?
Примером самодвойственной функции является функция XOR (исключающее ИЛИ). Она обладает свойством, что при инвертировании всех битов входа и выхода она остается неизменной. Другим примером является функция NOT (отрицание), которая инвертирует значение входного бита.