Понятие сечения многогранника: общая информация и основные принципы

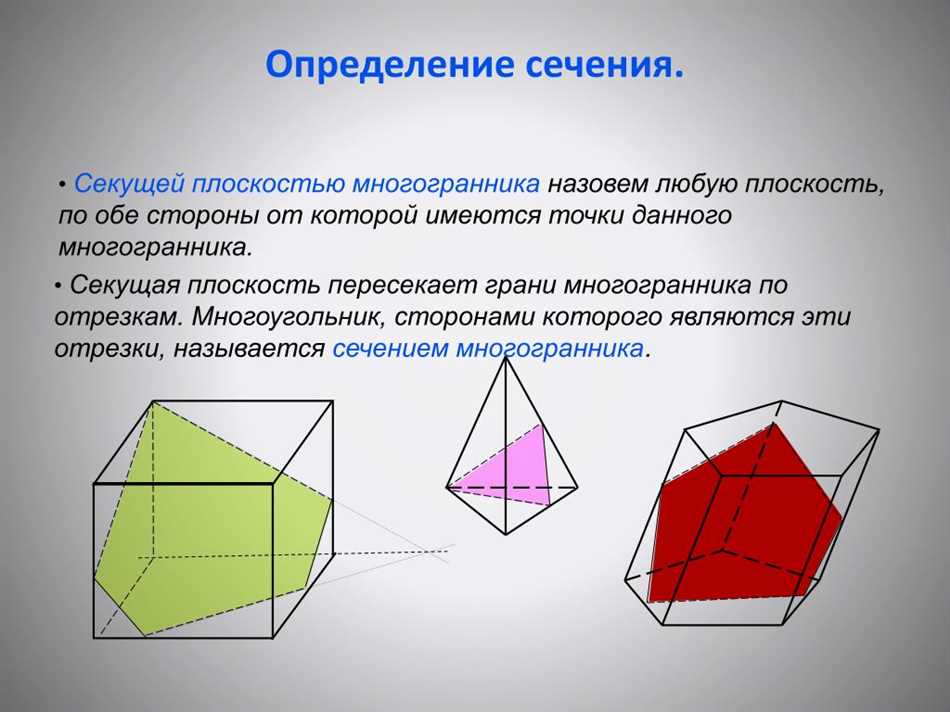
Сечение многогранника – это плоское пересечение многогранного тела, которое образует фигуру на его поверхности. Когда пронизывающая плоскость пересекает многогранник, она создает новую фигуру, которая называется секцией. Сечение может быть различной формы: круглым, овальным, треугольным и т.д., это зависит от положения и угла проникновения плоскости.

Сечение многогранников имеет важное значение для различных областей, таких как геометрия, строительство, архитектура и дизайн. Оно позволяет изучать внутреннюю структуру и свойства многогранников, а также предоставляет информацию о их внешнем виде. Сечение многогранников помогает нам более глубоко понять, анализировать и визуализировать различные формы и конструкции.

Сечение многогранника и его особенности

Ну а теперь давай углубимся в детали. Во-первых, обрати внимание, что сечение может выглядеть очень разнообразно в зависимости от того, как проводить плоскость относительно многогранника. Например, если ты проведешь плоскость параллельно одной из граней куба, то сечение будет точно таким же, как эта грань. Но если плоскость будет идти под каким-то углом, то сечение получится уже совершенно другим.

Еще одна интересная особенность сечений многогранников — это их свойства. Глядя на сечение, можно многое узнать о самом многограннике. Например, если сечение будет иметь форму окружности, то это может говорить о том, что многогранник — шар или около того. Или если сечение будет прямоугольником, то это может значить, что многогранник — параллелепипед.

В общем, сечение многогранника — это весьма интересная и полезная штука. Благодаря сечениям, мы можем лучше понять и визуализировать форму и структуру многогранников. Так что давай не будем останавливаться на поверхности и начнем исследовать мир сечений! Какими сечениями ты бы хотел заняться?

Понятие о сечении многогранника

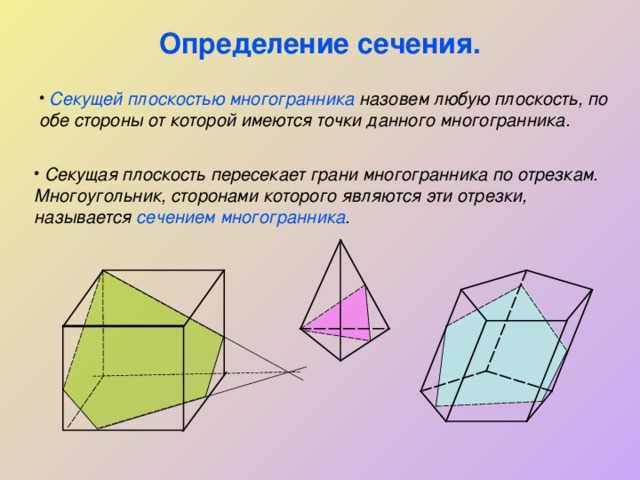
Зависит от того, как плоскость пересекает многогранник, сечение может быть разным. Иногда плоскость может проходить через вершины многогранника и создавать углы. Иногда она будет проходить через ребра и создавать отрезки. Все зависит от угла и направления плоскости относительно многогранника.

Сечение многогранника — это очень важное понятие в математике, которое используется для анализа форм и структуры многогранников. Изучая сечения, мы можем узнать больше о многограннике и его свойствах. Многогранники — это удивительная область математики, которая помогает нам понять и визуализировать пространство вокруг нас. И когда ты следующий раз будешь видеть многогранник, вспомни, что его можно разрезать на кусочки и изучить каждый из них отдельно!

Особенности сечения многогранника

Одна из особенностей сечения – это количество ребер, которые пересекают плоскость. При сечении некоторые ребра могут остаться полностью внутри многогранника, некоторые могут быть пересечены на частичном участке, а некоторые полностью пересекут плоскость. Это создает интересные геометрические формы и может быть использовано для создания уникальных и оригинальных дизайнерских решений.

Другой важной особенностью является форма и размер новой фигуры, полученной в результате сечения. Она может быть многоугольной, эллиптической, параллелограммом или любой другой формой, в зависимости от формы и расположения секущей плоскости относительно многогранника. Это позволяет создавать разнообразные формы и структуры, которые могут использоваться в архитектуре, дизайне и других областях.

И наконец, одной из самых интересных особенностей сечения является получение новых граней и вершин. Когда мы секаем многогранник, некоторые грани могут быть полностью пересечены и разделены на две части, создавая новые грани. Кроме того, некоторые вершины могут быть разделены на две или более вершин, что также добавляет новые элементы в структуру многогранника. Это даёт нам больше возможностей для создания уникальных и сложных форм.

В итоге, сечение многогранника – это удивительный процесс, который позволяет нам исследовать геометрические формы и создавать новые, уникальные фигуры. Он открывает перед нами множество возможностей для творчества и экспериментов. Какие формы ты бы захотел создать, секая многогранник?

Виды сечений многогранника

1. Параллельное сечение: плоскость параллельна одной из граней многогранника. В результате получается срез, который полностью повторяет одну из граней многогранника.

2. Перпендикулярное сечение: плоскость перпендикулярна одной из граней многогранника. В этом случае срез будет являться проекцией всего многогранника на эту плоскость.

3. Сечение под углом: плоскость проходит через многогранник под некоторым углом к его граням. Результатом такого сечения является срез, который представляет собой не просто повторение грани многогранника, а его измененное изображение.

4. Смещенное сечение: плоскость не параллельна и не перпендикулярна граням многогранника. В этом случае срез многогранника будет представлять собой комбинацию нескольких его граней.

В зависимости от выбранного вида сечения, мы можем получить различные представления о форме и структуре многогранника. Это может быть полезно при анализе и изучении многогранников в геометрии.

Плоское сечение

Что такое плоское сечение? Когда я впервые услышал этот термин, у меня возникло множество вопросов. Но, оказалось, что все довольно просто и логично.

Представь себе, что ты имеешь некий многогранник, например, куб. У него есть грани, ребра и вершины — все мы в школе это изучали, верно? Вот и плоское сечение — это просто пересечение этого многогранника плоскостью.

Но зачем всё это нужно? Я был удивлен, узнав, что плоское сечение играет огромную роль в различных областях, таких как архитектура, инженерия и даже в искусстве! Оно помогает нам лучше понять форму многогранника и изучить его свойства.

Также плоское сечение может быть полезным инструментом для расчета площади поверхности многогранника или определения объема. Например, если мы знаем площадь плоского сечения и длину многогранника, то сможем найти его объем.

Мне кажется, что плоское сечение — это как раз тот случай, когда математика и реальный мир пересекаются. Так что давайте вместе изучать и применять этот удивительный инструмент!

Проекционное сечение

Проекционное сечение помогает нам понять форму многогранника, его размеры и взаимное расположение его частей. Например, плоское сечение через параллельные лучи может дать нам информацию о внутренних структурах и полостях многогранника.

Однако, стоит помнить, что проекционное сечение имеет свои ограничения. Некоторые детали могут быть потеряны или искажены при проекции. Поэтому, для полного понимания многогранника, часто применяют комбинацию проекционных сечений с другими методами анализа, например, компьютерным моделированием или физическими моделями.

Как строить сечение многогранника

Представь, что ты встал перед каким-то многогранником. Может быть, это прямоугольный параллелепипед или пирамида. Неважно. Ты хочешь узнать, как выглядит сечение этого многогранника. Ну, это просто!

Первый шаг — возьми острый нож и разрежь многогранник вдоль плоскости, которая тебе интересна. Простое, правда? Но не забудь использовать воображение! Представь, что многогранник — это твердое тело, и ты делаешь разрез, чтобы взглянуть внутрь.

Когда ты разрежешь многогранник, увидишь, что внутри образовалось новое тело — это и есть сечение многогранника. Может быть, это будет плоская фигура, например, просто многоугольник. А может быть, это будет что-то более сложное, например, эллипс или гипербола.

Теперь, когда у тебя есть сечение многогранника, можешь изучать его свойства и формулировать интересные вопросы. Например, сколько углов у этого многоугольника? Какая площадь у этого эллипса? Эти вопросы сможешь решить, если применишь знания о геометрии и алгебре.

Разрезание многогранников — веселая и увлекательная игра. Ты можешь сделать несколько разрезов и посмотреть, как меняется сечение. Играй, экспериментируй, и ты узнаешь все больше о формах и фигурах. Удачи в твоих геометрических приключениях!

Используемые инструменты

1. Теория множеств и логика

Для изучения сечений многогранников необходимо обладать базовыми знаниями в области теории множеств и логики. Понимание принципов множественных операций и аксиоматической логики помогает анализировать свойства сечений и проводить логические рассуждения в процессе их изучения.

2. Геометрические методы

Для визуализации сечений многогранников и проведения геометрического анализа используются различные геометрические методы. Можно использовать простые инструменты, такие как линейка и циркуль, а также более сложные программы для компьютерной графики, позволяющие создавать трехмерные модели и рассчитывать их сечения.

3. Математические моделирование

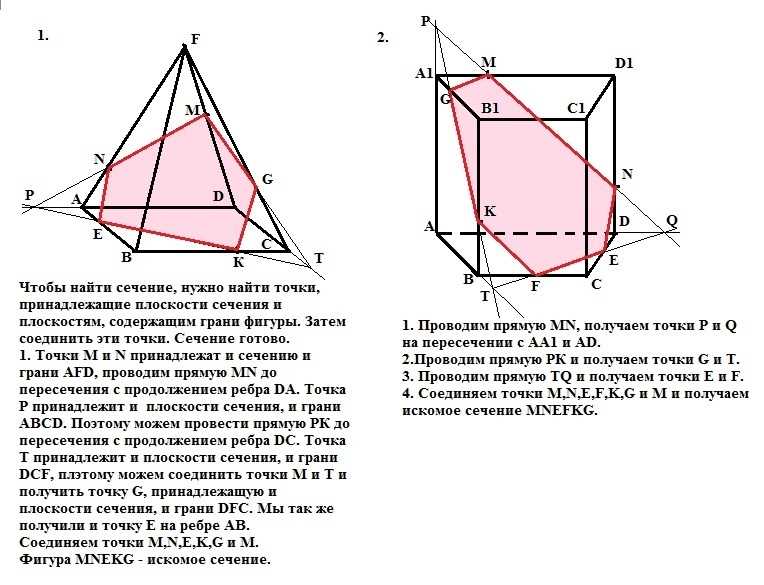
Для более точного анализа сечения многогранников часто применяются методы математического моделирования. С помощью математических моделей можно получить численные значения параметров сечений, а также провести анализ и сравнение различных сечений.

В целом, изучение сечений многогранников требует использования различных инструментов и методов. Опираясь на знания теории множеств и логики, а также используя геометрические методы и математическое моделирование, можно провести глубокий анализ и исследование сечений многогранников.