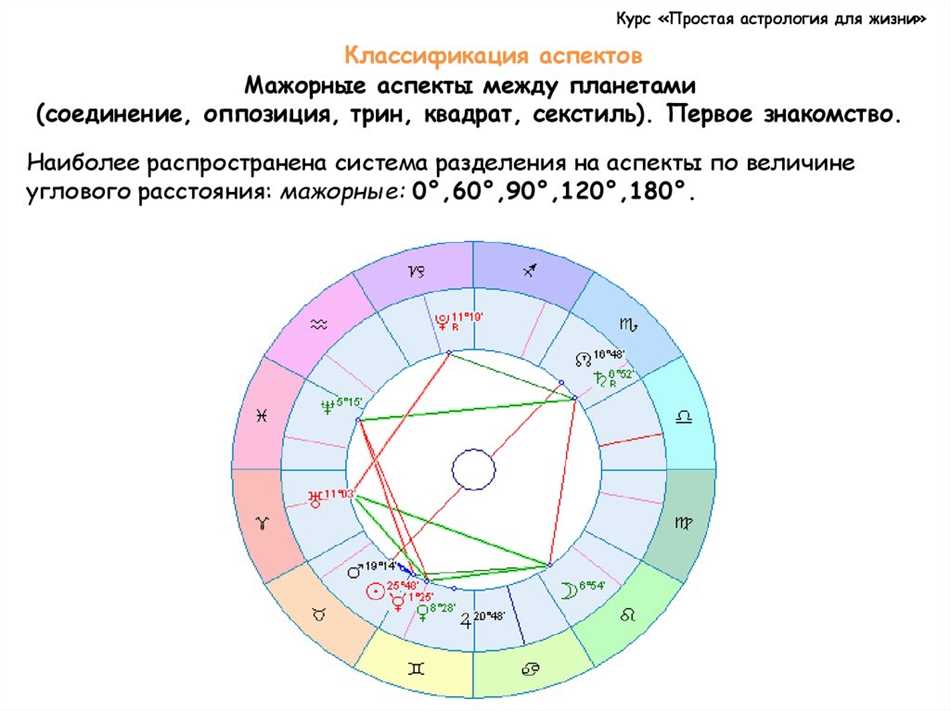
Секстиль и тригон — это два из нескольких геометрических аспектов в астрологии, которые используются для анализа аспектов между планетами в гороскопе.
Секстиль представляет собой угол 60 градусов между двумя планетами, который обычно считается благоприятным аспектом. Он указывает на гармонию, возможности для сотрудничества и обмена информацией.
Тригон — это угол 120 градусов, также считается благоприятным. Он указывает на энергию, силу и взаимодействие между планетами.
Астрологи используют эти аспекты для понимания взаимодействия планет и их влияния на личность. Они могут указывать на благоприятные периоды, возможности для роста и развития, а также наличие гармонии в различных аспектах жизни.
Понимание секстиля и тригона помогает астрологам создавать более точные гороскопы и предоставлять более детальные прогнозы.
Определение секстиля
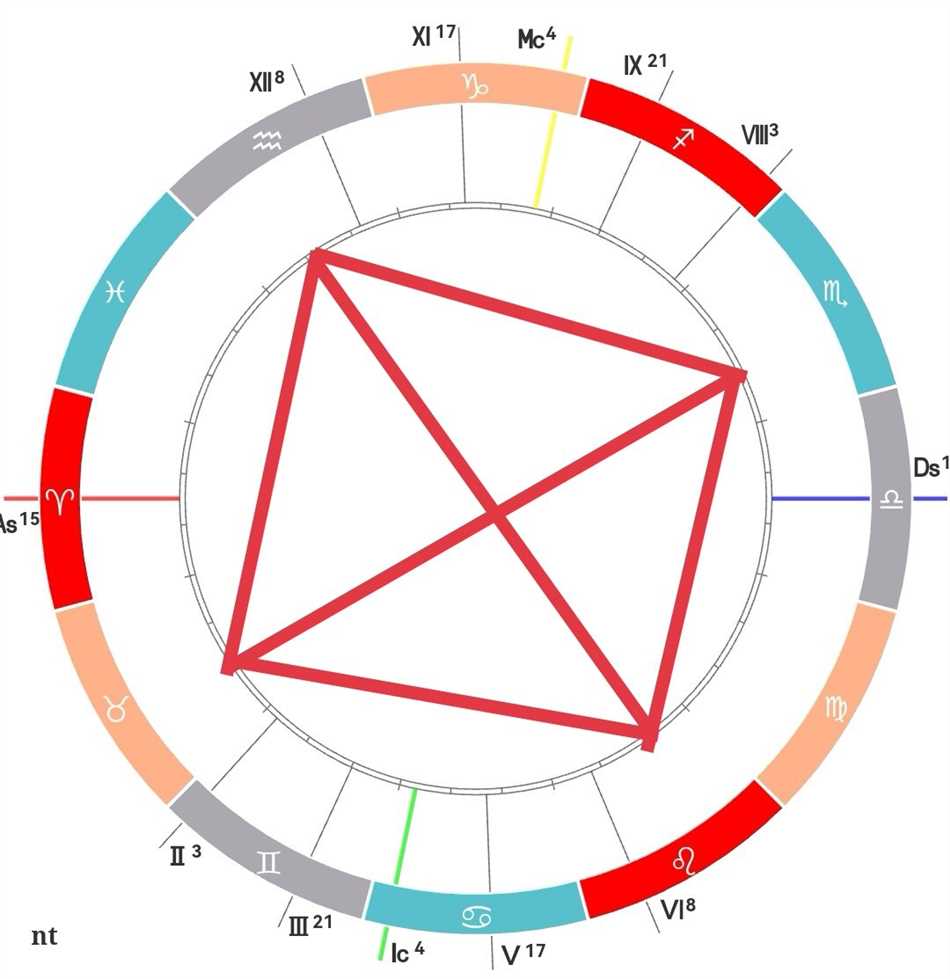
Секстиль представляет собой гармоничное взаимодействие между планетами, которое может привести к удачным событиям и благоприятным возможностям. Этот аспект приносит легкость, гибкость и умение находить компромиссы. Он помогает создать гармоничные отношения между людьми, улучшить коммуникацию и поддерживать мир и спокойствие.
Секстиль также может усилить интеллектуальные способности и таланты человека. Он может помочь в развитии творческого потенциала и способствовать достижению успеха в учебе или работе.
Весьма удачным может быть совместное сотрудничество людей, у которых в гороскопе есть секстили. Они могут легко договариваться и находить общий язык, что способствует совместной работе и достижению общих целей.
Применение секстиля

Секстиль часто рассматривается как благоприятный аспект, который может приносить вдохновение и творческую энергию. Он также может способствовать гармоничным взаимодействиям и легкости в общении.
Когда у вас есть секстиль между планетами в вашей натальной карте, это может указывать на то, что у вас есть естественный талант или способности в области, связанной с этими планетами. Например, секстиль между Солнцем и Венерой может указывать на художественный талант или способность привлекать людей.
Секстили также могут использоваться в астрологии для анализа текущих тенденций и прогнозирования будущих событий. Когда планеты образуют секстиль на диаграмме гороскопа, это может указывать на периоды возможностей, когда вам стоит поискать новые пути или развить свои таланты.
Итак, следующий раз, когда вы увидите секстиль на небе или в своей натальной карте, подумайте о том, как можно использовать эту энергию для реализации своих целей и мечтаний. А может быть, вы уже использовали эту энергию и достигли впечатляющих результатов? Расскажите мне об этом!
Определение тригона
Тригон… Кажется знакомым словом, не так ли? Вероятно, вы слышали его учительницу во время математического урока в школе. Но что же на самом деле означает это загадочное слово?
Тригон — это математический термин, который относится к изучению треугольников и их связи с углами и сторонами. Да, вы правильно поняли, тригонометрия — это область математики, которая исследует треугольники. Звучит немного страшно, не так ли? Но на самом деле, тригонометрия может быть довольно интересной и полезной.
Тригон обычно изучается в школьной программе в конце старшей школы. В этом разделе математики вы узнаете о таких понятиях, как синусы, косинусы и тангенсы. Эти функции вычисляются для углов в треугольнике и позволяют нам решать различные задачи, связанные с треугольниками. Например, вы можете использовать тригонометрию для определения длины неизвестной стороны треугольника или измерения высоты высокой горы.
Что ж, тригонометрия может быть сложной, но также очень увлекательной и полезной. Возможно, вы уже столкнулись с ней в повседневной жизни, даже не осознавая этого. Конечно, на самом деле, вы все равно приступить к изучению математики. Что касается меня, я уверен, что вы сможете преодолеть все препятствия и стать настоящим тригонометрическим гуру. Скажите, готовы ли вы взяться за треугольники и их углы?
Тригонометрические функции

Существует несколько основных тригонометрических функций, которые выразны через отношения сторон треугольника. Например, синус (sin) угла равен отношению противолежащей стороны к гипотенузе треугольника. Косинус (cos) угла равен отношению прилежащей стороны к гипотенузе, а тангенс (tan) угла – отношению противолежащей стороны к прилежащей.
Тригонометрические функции могут применяться для вычисления наклона склона, расстояния, скорости и других параметров в физических задачах. Они также используются для решения уравнений и моделирования.
Пример использования: Если мы знаем длину двух сторон треугольника и хотим найти угол между ними, мы можем использовать тригонометрическую функцию арктангенс (arctan). Это поможет нам найти значение этого угла.
Вопрос к читателю: Какие другие области применения тригонометрических функций вам известны? Какие примеры использования есть у вас в повседневной жизни?
Применение тригона в математике
Тригона, это такой математический раздел, который связан с изучением отношений между сторонами и углами треугольников. Сначала они выглядят такими простыми и невинными, но по мере углубления в материал, они могут стать сложными и запутанными. Однако не стоит паниковать! Тригона вы можете найти повсюду в нашем окружении: в архитектуре, инженерии, физике, астрономии и многих других областях.
Тригона был изначально разработан для работы с треугольниками, но его применение не ограничивается только ими. Он может использоваться для измерения дальности, высоты и углов в различных объектах и окружающей среде. Например, если вы хотите измерить высоту дерева, но не можете подняться на него, вы можете использовать тригональные расчеты, измеряя углы и расстояния от определенных точек.
Тригонометрия также широко применяется в графиках и моделировании, которые используются в компьютерной графике и играх. Отображение 3D-объектов и анимаций требует точного понимания тригонометрии для правильного расчета перспективы и перемещения объектов.
В общем, тригонометрия безусловно полезна и интересна. Использование тригонометрии позволяет нам лучше понять мир, исследовать его и создавать новые возможности. Так что давайте не забывать о тригональных функциях и углах, ведь они могут быть не только важными для нашего образования, но и применимыми в нашей повседневной жизни!
Тригонометрия в геометрии
Когда мы говорим о тригонометрии в геометрии, мы обычно имеем в виду прямоугольные треугольники. Они особенно интересны, потому что они имеют прямой угол в 90 градусов, что делает их такими удобными для изучения. Важные тригонометрические понятия, такие как синус, косинус и тангенс, помогают нам определить отношение между углами и сторонами треугольника.
Например, если нам известна длина одной стороны и угол прилегающий к этой стороне, мы можем использовать тригонометрию, чтобы найти длину другой стороны треугольника. Это очень полезно, когда нам нужно измерить расстояния или высоты, и у нас нет возможности измерить их прямо.
Так что тригонометрия — это наш главный помощник в геометрии. Она позволяет нам легче измерять и понимать наши треугольники и использовать их для решения различных задач. Без тригонометрии, геометрия была бы гораздо сложнее и менее увлекательной! Не забывайте использовать тригонометрию в своих геометрических приключениях!