В математике сектор – это участок окружности, ограниченный двумя радиусами и дугой между ними. Он может быть описан как фигура, имеющая начальную и конечную точки на окружности и угол между ними.
Секторы имеют свои особенности и применяются в разных областях. Например, в геометрии они используются для вычисления площади окружности или для изучения соотношений между различными углами. В графике они могут представлять процентное соотношение частей целого. А в тригонометрии секторы помогают определить значения тригонометрических функций и решить различные задачи.
В общем, сектор – это удобное понятие, которое помогает нам разбираться в сложных математических ситуациях и применять его на практике.
Определение
Чтобы понять, что такое сектор, давай рассмотрим пример. Представим, что у нас есть окружность с центром в точке O и радиусом 5 см. Пусть A и B — это две точки на этой окружности. Если мы соединим точки A и B с центром O, то получим радиусы окружности. Если угол между этими радиусами равен 60 градусам, то сектор будет состоять из дуги AB и двух радиусов.
Секторы используются в различных областях, например, в геометрии, физике, космологии и т. д. Они помогают нам понять, какие пространственные области существуют, и делают наши вычисления более точными и понятными.
Свойства сектора в математике
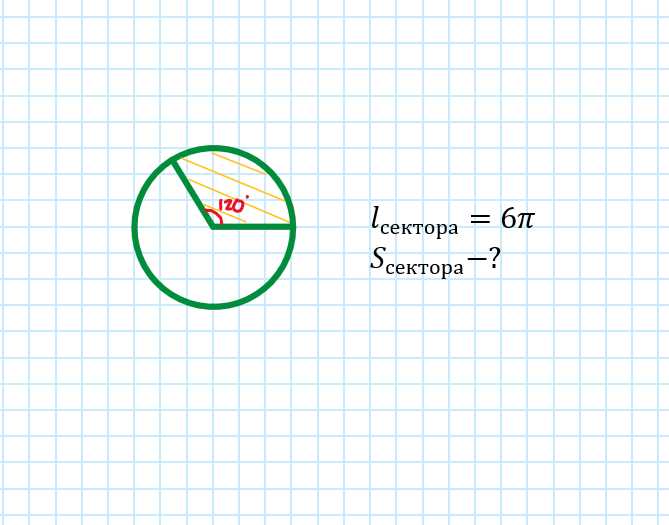
Первое свойство сектора — его площадь. Площадь сектора можно вычислить, используя формулу S = (π * r² * α) / 360, где S — площадь сектора, r — радиус круга, а α — центральный угол сектора. Эта формула позволяет нам определить, сколько площади занимает сектор от всего круга.
Второе свойство сектора — его длина окружности. Длина окружности сектора можно найти, используя формулу L = (2 * π * r * α) / 360, где L — длина окружности сектора. Эта формула помогает нам определить, какую длину занимает дуга сектора.
Третье свойство сектора — его угол. Угол сектора можно вычислить, используя формулу α = (L * 360) / (2 * π * r), где α — центральный угол сектора. Это свойство позволяет нам определить, насколько градусов повернута дуга сектора.
Таким образом, свойства сектора помогают нам анализировать и понимать его характеристики, что пригождается при решении различных геометрических задач и задач из реального мира.
Вычисление площади
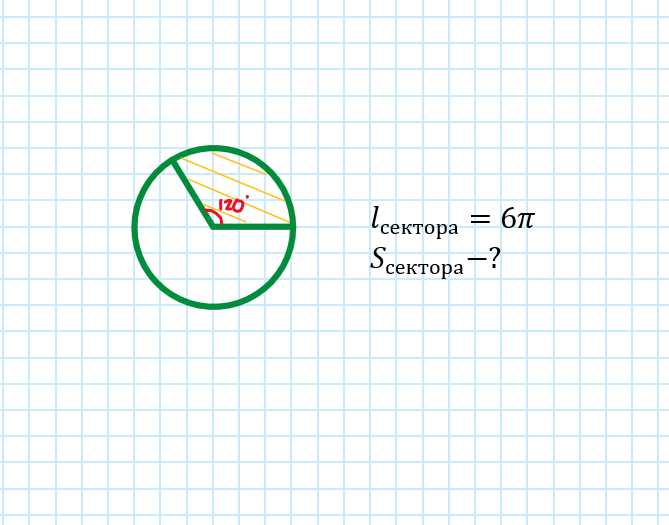
Когда мы говорим о вычислении площади, мы обычно имеем в виду определение площади фигуры или поверхности. Это важный аспект в математике и геометрии, который помогает нам понять, сколько пространства занимает объект.
Если мы хотим вычислить площадь прямоугольника, мы знаем, что площадь равна произведению его длины на ширину. Но что делать, если фигура имеет нестандартную форму, например, круг или треугольник? В таких случаях нам нужно использовать соответствующие формулы для вычисления площади.
Для вычисления площади круга нам нужно знать его радиус. Формула для вычисления площади круга — это π (пи) умноженное на квадрат радиуса. Пи — это математическая константа, приближенное значение которой округлили до 3,14.
А как насчет треугольников? Мы можем использовать формулу для вычисления площади треугольника, известную как «полупроизведение основания на высоту». Это означает, что мы умножаем длину основания треугольника на его высоту, а затем делим полученное значение пополам.
- Прямоугольник: Длина × Ширина
- Круг: π × (Радиус)^2
- Треугольник: (Основание × Высота) ÷ 2
Знание этих формул для вычисления площади поможет нам решать различные задачи и применять их в реальной жизни. Например, если у вас есть участок земли, и вы хотите знать, сколько площади в нем, вам будет полезно знать эти формулы.
Так что, в следующий раз, когда вы столкнетесь с задачей на вычисление площади, не бойтесь! Примените соответствующую формулу и вы сможете найти ответ. Ведь математика — это такой великолепный и универсальный инструмент, который помогает нам разгадывать головоломки нашей физической реальности!
Заключение: Примеры использования
Сектор, который представляет собой часть круга, используется в различных областях математики и физики. Рассмотрим несколько примеров его применения:
- Геометрия: В геометрии секторы используются для измерения углов и площадей. Например, для нахождения площади сектора необходимо знать радиус и центральный угол. Это помогает в решении задач по нахождению площадей фигур и расчету долей площади от общей площади.
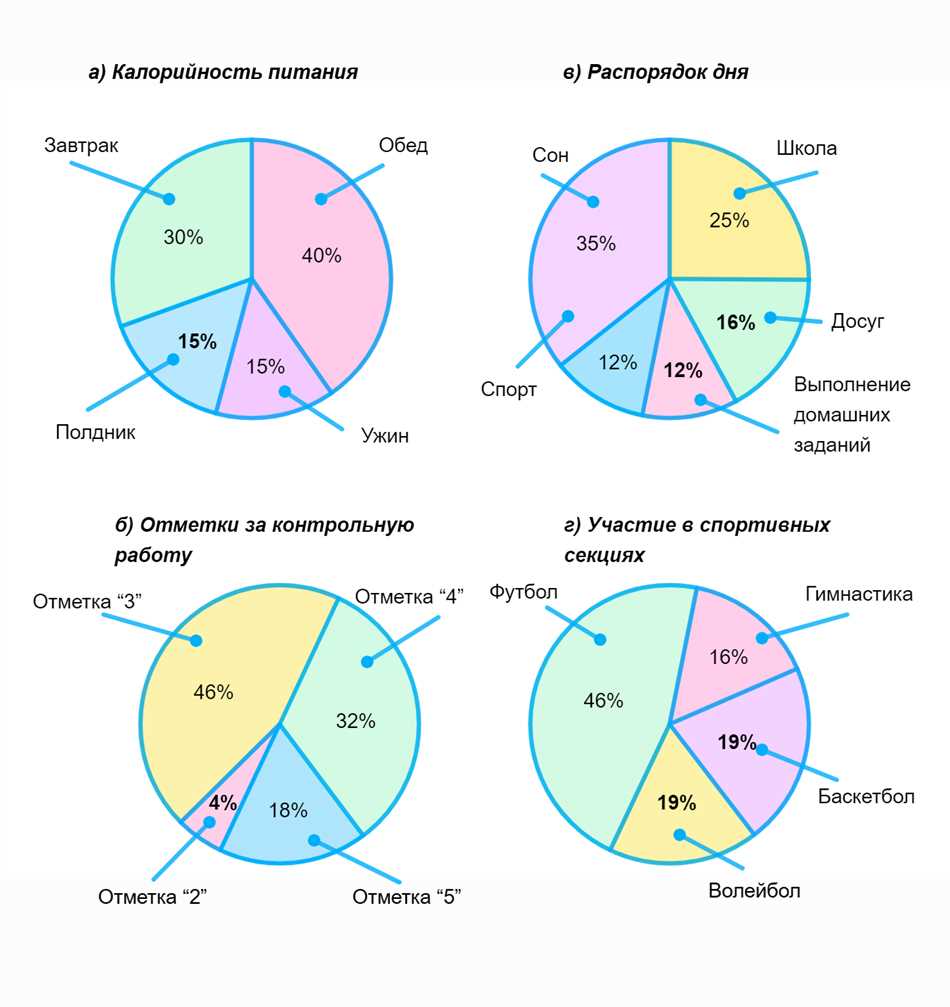
- Статистика: В статистике секторы используются для визуализации долей или процентного соотношения различных категорий или групп данных. Диаграммы секторов (или круговые диаграммы) являются популярным инструментом для представления статистических данных.
- Физика: В физике секторы используются для анализа движения тел. Например, при изучении кругового движения, для определения углового перемещения и скорости объекта, используются секторы. Это позволяет более точно описать и анализировать движение объекта.
Это только некоторые примеры использования секторов в математике и физике. Они являются мощным инструментом, позволяющим более точное измерение и анализ различных явлений и процессов.
Вопрос-ответ:
Какие примеры использования могут быть для новой программы?
Примеры использования новой программы могут быть разными в зависимости от ее функционала. Например, если это программный продукт для учета финансовых операций, то он может быть использован бухгалтерами для ведения учета, руководителями компании для анализа финансовых показателей и т.д. Если это графический редактор, то он может быть использован дизайнерами для создания и редактирования графических элементов, художниками для создания иллюстраций и т.д. В общем, примеры использования программы зависят от ее назначения и функционала.
Какие примеры использования современных технологий в медицине?
Примеры использования современных технологий в медицине многочисленны. Например, разработка программ для анализа медицинских данных позволяет врачам более эффективно проводить диагностику и выбирать оптимальные методы лечения. Использование робототехники позволяет проводить сложные операции с максимальной точностью и минимальными рисками для пациента. Виртуальная реальность используется для обучения медицинского персонала и симуляции хирургических операций. Также активно применяются мобильные приложения для контроля состояния здоровья, приема лекарств и своевременного обращения к врачу. В целом, современные технологии значительно улучшают качество медицинской помощи и повышают эффективность лечения.
Какие примеры использования искусственного интеллекта в бизнесе?
Примеры использования искусственного интеллекта в бизнесе многочисленны. Одним из них является автоматизация процессов в компаниях. Благодаря искусственному интеллекту можно создать программы, которые будут выполнять рутинные задачи, освобождая сотрудников от монотонной работы и увеличивая их продуктивность. Например, искусственный интеллект может быть использован для автоматизации обработки заявок или для предсказания спроса на товары. Также искусственный интеллект может быть использован для анализа больших объемов данных и выявления скрытых закономерностей и тенденций. Например, в банковской сфере искусственный интеллект может быть использован для выявления финансовых мошенничеств или для предсказания риска невыплаты кредита. В целом, использование искусственного интеллекта в бизнесе помогает улучшить эффективность работы и принять более обоснованные решения.