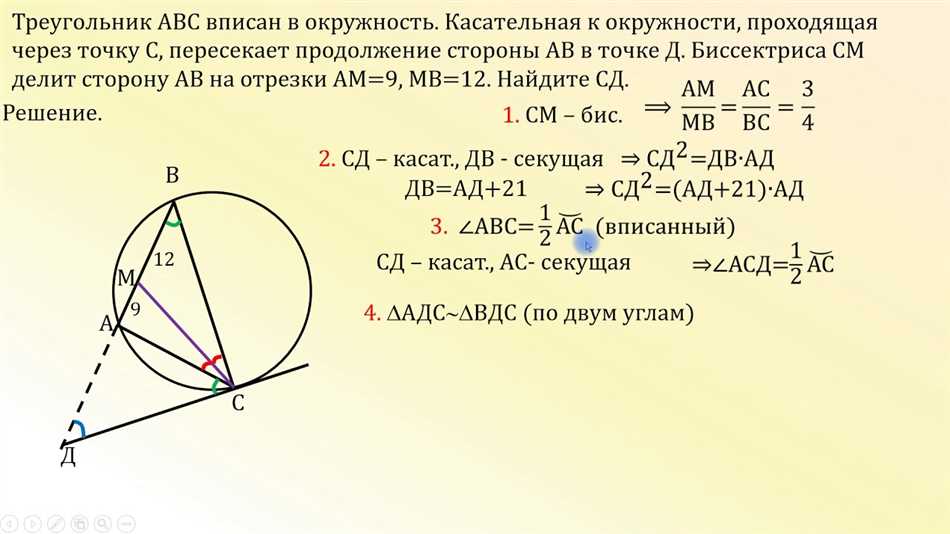
Секущая — это линия или отрезок, который пересекает окружность в двух или более точках. Она может проходить через центр окружности или быть непараллельной ей. Секущая приводит к образованию дуги окружности и двух хорд, которые являются ее отрезками. Секущая имеет свойство пересекать радиусы окружности под прямыми углами. Использование секущих позволяет решать различные задачи в геометрии: определение длины дуги, построение треугольника, через который проходит окружность и т.д. От понимания секущей и ее свойств зависит решение множества геометрических задач и построение сложных фигур на плоскости.
Определение секущей в геометрии окружности
Секущая — это прямая линия, которая пересекает окружность в двух точках. Другими словами, она проходит сквозь окружность и имеет два пересечения с её границей. Когда мы говорим о секущей, мы обращаемся к особенной геометрической связи между прямой линией и окружностью.
Секущая может быть положительной или отрицательной. Положительная секущая пересекает окружность с двух сторон, в то время как отрицательная секущая пересекает ее только один раз.
Секущая имеет большое значение в геометрии, поскольку она помогает нам понять различные свойства и взаимосвязи между окружностью и другими фигурами. Она также используется для нахождения углов и длин отрезков внутри и вне окружности.
Теперь, когда мы знаем определение секущей в геометрии окружности, давайте посмотрим на примеры и узнаем больше о ее свойствах и применениях!
Основные понятия

Теперь перейдем к понятию секущей. Секущая – это прямая, которая пересекает окружность в двух точках. Секущая может иметь разные положения относительно окружности: она может быть касательной (пересекать окружность в одной точке), пересекать окружность внутри нее или пересекать ее снаружи.
Зачем нам нужно знать о секущих? Это понятие используется во многих областях, таких как геометрия, физика, инженерия и даже компьютерная графика. Например, в физике секущая может представлять силу, действующую на объект, движущийся по окружности.
Итак, секущая в геометрии окружности — это прямая, пересекающая окружность в двух точках. Это важное понятие с множеством применений и связей с другими областями знаний.
Уравнение секущей в геометрии окружности
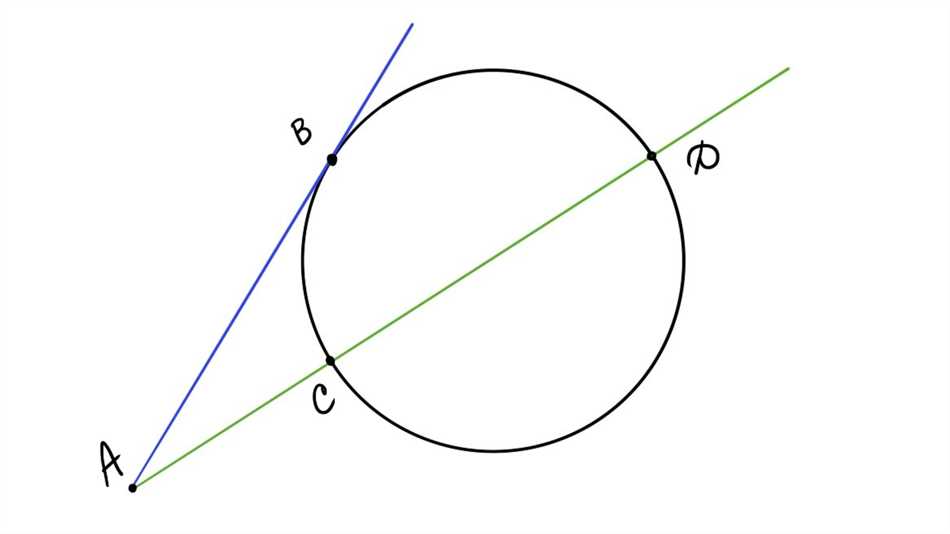
Для того чтобы найти уравнение секущей, необходимо знать координаты двух точек, через которые она проходит. Пусть точки A(x1, y1) и B(x2, y2) — это точки пересечения секущей и окружности.
Уравнение секущей можно записать в виде:
(x — x1)(x — x2) + (y — y1)(y — y2) = 0
Это уравнение задает все точки прямой, проходящей через точки A и B. Если это уравнение выполняется для точки M(x, y), то значит, что точка М лежит на секущей, а значит, эта прямая пересекает окружность.
Таким образом, уравнение секущей позволяет нам определить положение прямой относительно окружности и найти точки ее пересечения с окружностью.
Теоремы о секущих
Что такое секущая в геометрии окружности? Представь себе круг, а теперь нарисуй через него прямую линию. Вот эта линия и называется секущей. Она пересекает окружность в двух точках.
Интересно, что секущие имеют свои теоремы. Первая теорема гласит, что если две секущие пересекаются внутри окружности, то произведения отрезков секущих, ведущих от пересечения секущих до точек пересечения с окружностью, равны. Вторая теорема утверждает, что если секущая пересекает окружность во внешней точке, то произведение отрезков секущей, ведущих от пересечения секущей с окружностью до внешней точки и до ближайшей пересекающей секущую, также равно.
А ты думаешь, что эти теоремы просто так созданы? Конечно же, нет! Ученые годами изучали окружности и открыли эти закономерности. Теперь ты сам можешь применять эти теоремы для решения геометрических задач. И помни, математика – это не только сложно, но и интересно!
Заключение
Пример 1:
Пусть у нас есть окружность с центром O и радиусом r. Проведем две секущие AB и CD, пересекающиеся в точке E. Если известны длина отрезков AE и BE, можно найти длину отрезков CE и DE с помощью теоремы секущих:
CE × DE = AE × BE
Это свойство секущих очень полезно при решении задач на нахождение отрезков, пересекающихся с окружностью.
Пример 2:
Пусть у нас есть окружность с центром O и радиусом r. Проведем две секущие AB и CD, пересекающиеся в точке E. Если известна длина отрезка CE и угол CED, можно найти длину отрезка DE с помощью теоремы секущих:
DE = CE × cot(∠CED/2)
Это свойство секущих помогает находить длину отрезков, пересекающихся с окружностью, если известен угол между секущей и касательной в точке пересечения.
В данной статье мы рассмотрели только два примера использования секущих в геометрии окружности. В действительности, свойства секущих имеют широкий спектр применений и активно используются в различных задачах и теоремах геометрии. Понимание этих свойств поможет вам лучше разобраться в данной теме и с легкостью решать задачи, связанные с секущими.