Понятие следствия в математике: определение и примеры

Когда мы решаем математическую задачу, мы применяем различные методы и операции, чтобы прийти к правильному ответу. Однако в процессе решения часто возникают дополнительные утверждения, которые следуют из наших исходных условий и шагов решения. Именно эти дополнительные утверждения называются следствиями в математике.

Важно отметить, что следствия не всегда очевидны и требуют логического мышления и анализа. Они помогают нам лучше понять и описать свойства и отношения в математике, а также применять их в различных областях науки и техники.

Следствие в математике: план статьи

Следствие — это как результат логического рассуждения. Когда мы знаем некоторый набор фактов или теорем, мы можем использовать их, чтобы получить новые утверждения. В математике следствия позволяют нам расширять наши познания и строить более сложные модели и теории.

Математические следствия могут быть как простыми, так и сложными. Они могут быть следствиями простых уравнений или графиков функций, а иногда требуют применения более сложных математических инструментов, таких как математическая логика или алгебраическая геометрия.

Так как мы можем использовать следствия, чтобы получить новые знания, это позволяет нам строить все более сложные и точные математические модели, которые могут применяться во многих областях науки и жизни. Например, математические модели используются в физике для описания движения тел и в экономике для прогнозирования роста и падения цен.

Когда мы решаем математическую задачу, мы обычно оперируем не только известными фактами, но и используем следствия, чтобы получить новые результаты. Это позволяет нам находить элегантные и эффективные решения для сложных проблем.

Итак, следствия в математике — это наш способ расширить наши знания и построить более точные и полезные модели. Они позволяют нам идти дальше и исследовать глубже. Давайте вместе погрузимся в мир математических следствий и расширим наши границы знания. Что думаете об этом?

Определение

Когда мы решаем математическую задачу или доказываем теорему, мы строим цепочку логических рассуждений от известных данных к неизвестному утверждению. При этом мы используем уже доказанные теоремы или следствия. Следствие может быть индуктивным, если оно следует из конечного множества истинных утверждений, или дедуктивным, если оно следует из основных аксиом и определений.

Примером следствия может быть утверждение «Если сумма двух чисел равна 10, то каждое из них не может быть больше 10». Это следствие следует из свойств и аксиом арифметики и может быть легко доказано с помощью логических рассуждений.

Свойства следствия

• Независимость: Следствие не зависит от контекста или исходных данных. Оно справедливо везде и всегда при условии соблюдения основных правил и аксиом.
• Структурированность: Следствие может быть представлено в удобной форме с помощью таблиц, диаграмм или других графических средств. Это помогает наглядно представить логическую цепочку рассуждений и увидеть все связи.

Различие между следствием и теоремой

Когда мы говорим о математике, часто вспоминаем о теоремах и следствиях. Но в чем их различие? Давайте разберемся.

Теорема – это утверждение, которое было доказано и считается верным. Теоремы являются основными строительными блоками математических теорий и они обычно имеют важное значение в области, к которой они относятся. Теоремы могут быть простыми или сложными, но они все имеют одну общую черту – они доказаны.

Важно помнить, что теорема и следствие – это непрерывный процесс в математике. Чем больше мы изучаем и доказываем, тем больше теорем и следствий мы можем открыть.

Примеры следствий в математике

• Следствие из теоремы Пифагора: Если квадрат числа делится на 3, то само число также делится на 3. Например, 9 — квадрат числа 3, и он делится на 3.
• Следствие из определения угла: Сумма углов внутри треугольника равна 180 градусам. Например, если мы знаем, что два угла треугольника равны 60 градусам, мы можем использовать это следствие, чтобы найти остающийся угол: 180 — 60 — 60 = 60.
• Следствие из теоремы Ферма: Уравнение x^n + y^n = z^n не имеет целых решений при n>2. Это следствие является результатом более общей теоремы Ферма, которая не была доказана в течение долгого времени.
• Следствие из геометрической прогрессии: Если первый член прогрессии равен 1 и знаменатель меньше 1, то сумма всех членов прогрессии равна 1/(1-знаменатель). Например, для прогрессии 1/2, 1/4, 1/8, … сумма всех членов равна 1/(1-1/2) = 2.

Это только небольшой набор примеров следствий в математике. Математика полна интересных и удивительных следствий, которые позволяют нам лучше понимать и описывать мир вокруг нас.

Доказательство следствий

В процессе доказательства следствия мы используем различные математические методы, логику и рассуждения. Основная идея доказательства заключается в том, чтобы привести серию логических шагов, которые приводят от уже известных фактов к новому утверждению. Для этого мы используем логические законы и рассуждения от противного.

Одним из ключевых понятий в доказательстве следствий является «доказательство от противного». Идея заключается в том, что мы предполагаем, что утверждение, которое мы хотим доказать, неверно, и пытаемся найти противоречие или несоответствие этому предположению. Если нам удается найти такое противоречие, то это означает, что исходное утверждение верно.

Важно понимать, что доказательство следствия не является абсолютной истиной или доказательством независимо от контекста. Оно зависит от уже принятых аксиом или доказанных фактов. Иногда мы можем доказать следствие, но оно может быть неверно в других условиях или с другими аксиомами. Поэтому необходимо быть внимательными и внимательно анализировать все предпосылки и условия задачи.

Доказательство следствий — это важный и понятийный процесс в математике, который помогает нам строить новые знания на основе уже известных утверждений и фактов. Оно требует логического мышления, анализа и умения применять математические методы. При этом оно также может быть интересным и увлекательным опытом, который развивает наши интеллектуальные способности и способствует развитию математической интуиции.

Важность следствий в математических исследованиях

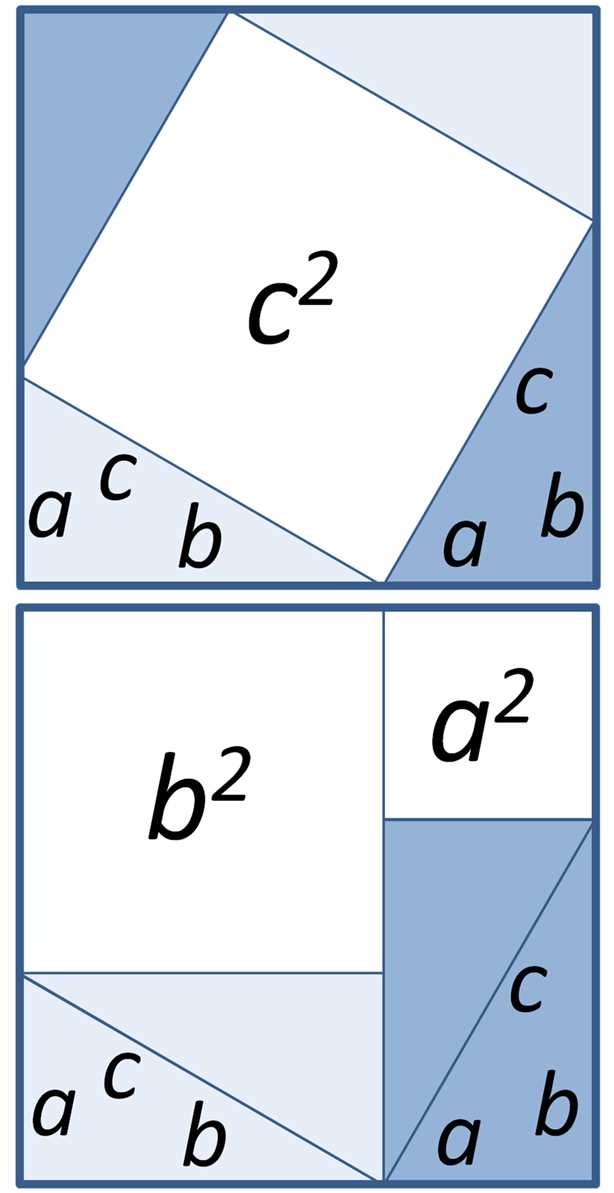
Первая причина, по которой следствия являются важными в математических исследованиях, — это их способность устанавливать новые связи между уже известными фактами. Следствия позволяют нам обобщить конкретные случаи и узнать, действительно ли они являются частью более общего закона или правила. Это позволяет придать математическим теориям большую универсальность и применимость.

Вторая причина, по которой следствия важны, — это их способность выявлять противоречия, неполноту или ошибки в уже установленных теориях. В случае, если из определенных аксиом и определений следуют неверные утверждения или противоречия, это может указывать на неправильность начальных предположений или необходимость уточнить их.

Третий аспект важности следствий в математических исследованиях заключается в их применении в решении практических задач. Они помогают в разработке новых методов и алгоритмов, а также в нахождении оптимальных решений в различных областях науки, техники и экономики. Результаты, полученные в математических исследованиях, часто находят свое применение в решении сложных реальных проблем.

Таким образом, следствия в математических исследованиях играют важную роль в развитии и применении математики. Они позволяют уточнить уже известные факты, обобщить конкретные случаи, выявить противоречия и ошибки, а также применить математические методы в решении практических задач. Без следствий математика не смогла бы достигать такого высокого уровня точности и достоверности.