Правила смены знака неравенств

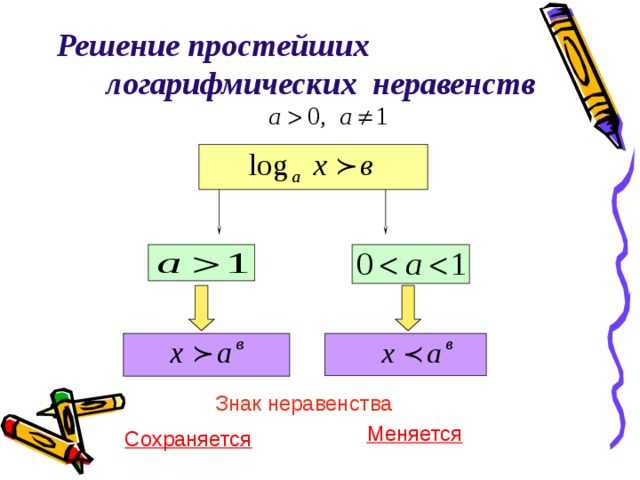
Чтобы понять, при каких условиях меняется знак неравенства, необходимо углубиться в основы математики. Когда мы сравниваем два числа, то можем получить одно из трех возможных отношений: равенство, неравенство или неопределенность. Если числа равны, то знак неравенства не меняется, они остаются равными. Но если числа разные, то все зависит от их сравнения друг с другом. Если первое число больше второго, то мы обозначаем это знаком «>», и знак неравенства сохраняется. Но если второе число больше первого, то мы используем знак «<" и меняем знак неравенства на противоположный. Таким образом, знак неравенства меняется в случае, когда второе число больше первого.

Общая информация

Важно понимать, что в зависимости от значения переменных или констант, знак неравенства может меняться. Изучение условий, при которых это происходит, является ключевым в математике и алгебре.

Когда уравнение содержит знаки сравнения, такие как ‘>’, ‘<', '≥' или '≤', оно называется неравенством. Неравенства могут быть строгими или нестрогими. Строгие неравенства обозначаются знаками '>‘, ‘<', а нестрогие - '≥' и '≤'.

• Знак ‘>’, который читается как «больше», указывает на то, что левая часть неравенства больше правой.
• Знак ‘<', который читается как "меньше", указывает на то, что левая часть неравенства меньше правой.
• Знак ‘≥’, который читается как «больше или равно», указывает на то, что левая часть неравенства больше или равна правой.
• Знак ‘≤’, который читается как «меньше или равно», указывает на то, что левая часть неравенства меньше или равна правой.

Теперь, когда мы вспомнили основные понятия, давайте рассмотрим подробнее, при каких условиях меняется знак неравенства.

Меняется знак при умножении или делении на отрицательное число

Представьте себе два числа: одно положительное, а другое отрицательное. Если мы умножим эти два числа, то получим отрицательное число. Например, 3 умножить на -2 даёт -6. И наоборот, если у нас есть отрицательное число и мы умножаем его на положительное, то также получаем отрицательное число.

То же самое происходит и при делении. Если положительное число разделить на отрицательное, получаем отрицательный результат. Например, 6 делить на -3 даёт -2. И наоборот, если отрицательное число разделить на положительное, также получаем отрицательное число.

Понятно, что умножение или деление на отрицательное число меняет знак числа. То есть, если у нас есть неравенство, и мы умножаем или делим обе его части на отрицательное число, то знак неравенства меняется на противоположный.

Давайте рассмотрим это на примерах:

• Если у нас есть неравенство 5 > 3 и мы поделим обе его части на -1, получим -5 < -3. Знак неравенства поменялся.
• Если у нас есть неравенство -4 < 2 и умножим обе его части на -2, получим 8 > -4. Знак неравенства также поменялся.

Таким образом, меняется знак неравенства при умножении или делении на отрицательное число. Это основное правило, которое помогает нам понять, как ведет себя неравенство при математических операциях.

Меняется знак при взятии обратного значения

Вы, наверное, знакомы с неравенствами. Они используются, чтобы сравнить значения двух выражений и указать, какое из них больше или меньше. Но что происходит, когда мы берем обратное значение обоих выражений? Оказывается, что знак неравенства меняется! Это важное свойство неравенств, оно помогает нам понять, как изменится результат, когда мы меняем направление сравнения.

Давайте рассмотрим пример: у нас есть неравенство a < b. Это означает, что значение a меньше значения b. Но что произойдет, если мы возьмем обратное значение обоих выражений? То есть, если мы возьмем обратное значение a и обратное значение b? Получим -a > -b.

Здесь мы видим, что знак неравенства изменился. Изначально у нас было <, а теперь у нас >. Это произошло потому что мы взяли обратные значения обоих выражений. Такое свойство вызывает инвертирование знака неравенства.

Иначе говоря, если мы знаем, что a < b, то можем сказать, что -a > -b. Это обратное значение неравенства.

Теперь давайте применим это знание к решению задач. Предположим, что у нас есть уравнение 2x > 6. Мы можем разделить обе стороны на 2 и получить x > 3. Здесь мы взяли обратное значение 2x и 6, и знак неравенства поменялся. Теперь мы знаем, что x должно быть больше 3, чтобы уравнение было истинным.

Таким образом, когда мы берем обратные значения обоих выражений в неравенстве, знак неравенства меняется. Это важное свойство неравенств, которое помогает нам понять, как изменится результат, когда мы меняем направление сравнения. Надеюсь, этот небольшой материал поможет вам лучше понять, как и почему меняется знак неравенства при взятии обратного значения. Успехов вам в изучении математики!

Меняется знак при возведении в чётную степень

Знак неравенства может меняться в зависимости от различных условий и правил математики. Одно из таких правил заключается в том, что знак неравенства меняется при возведении в чётную степень.

Давайте рассмотрим пример, чтобы лучше понять это правило:

• Пусть у нас есть неравенство x < 0, где x — любое отрицательное число.
• Если мы возведём это неравенство в чётную степень, например, во вторую степень, то получим x^2 > 0.

Теперь посмотрим на пример с положительным числом:

• Пусть у нас есть неравенство y > 0, где y — любое положительное число.
• Если мы возведём это неравенство в чётную степень, например, во вторую степень, то получим y^2 > 0.

Из этих примеров видно, что знак неравенства не меняется при возведении в чётную степень, если исходное число отрицательное или положительное.

Однако, если исходное число равно нулю, то знак неравенства сохраняется, даже при возведении в чётную степень. Например, для неравенства z ≥ 0, если мы возведём его во вторую степень, то получим z^2 ≥ 0.

При каких условиях меняется знак неравенства

Итак, рассмотрим условия, при которых меняется знак неравенства:

1. Когда обе части неравенства умножаются или делятся на отрицательное число, то знак неравенства меняется на противоположный. Например: если дано неравенство 2x > 6, то делим его обе части на 2 и получаем x < 3.
2. Когда обе части неравенства умножаются или делятся на положительное число, знак неравенства остается без изменений. Например: если дано неравенство 3x < 9, то делим его обе части на 3 и получаем x < 3.
3. Когда обе части неравенства умножаются или делятся на ноль, неравенство теряет смысл и не имеет решений.
4. Когда обе части неравенства сравниваются с нулем по разные стороны, то знак неравенства меняется на противоположный. Например: если дано неравенство 2x — 3 > x + 4, то вычитаем x и 3 из обеих частей и получаем x > 7.
5. Когда обе части неравенства складываются или вычитаются с положительным числом, знак неравенства остается без изменений. Например: если дано неравенство 3x + 5 < 2x + 7, то вычитаем 2x и 5 из обеих частей и получаем x < 2.