Для пятоклассников разряды в математике могут звучать сложно, но на самом деле это не так уж и сложно. Разряды – это группы чисел, которые при записи имеют одинаковое положение в числе. Чтобы лучше понять эту тему, давайте рассмотрим несколько примеров.
Например, число 583. Здесь первый разряд – сотни, второй – десятки, третий – единицы. То есть, цифра в первом разряде показывает, сколько сотен в числе, во втором – сколько десятков, а в третьем – сколько единиц.
Разряды в математике помогают нам легче понять и обрабатывать большие числа. Теперь, когда вы знаете, что такое разряды, давайте приступим к их практическому использованию!
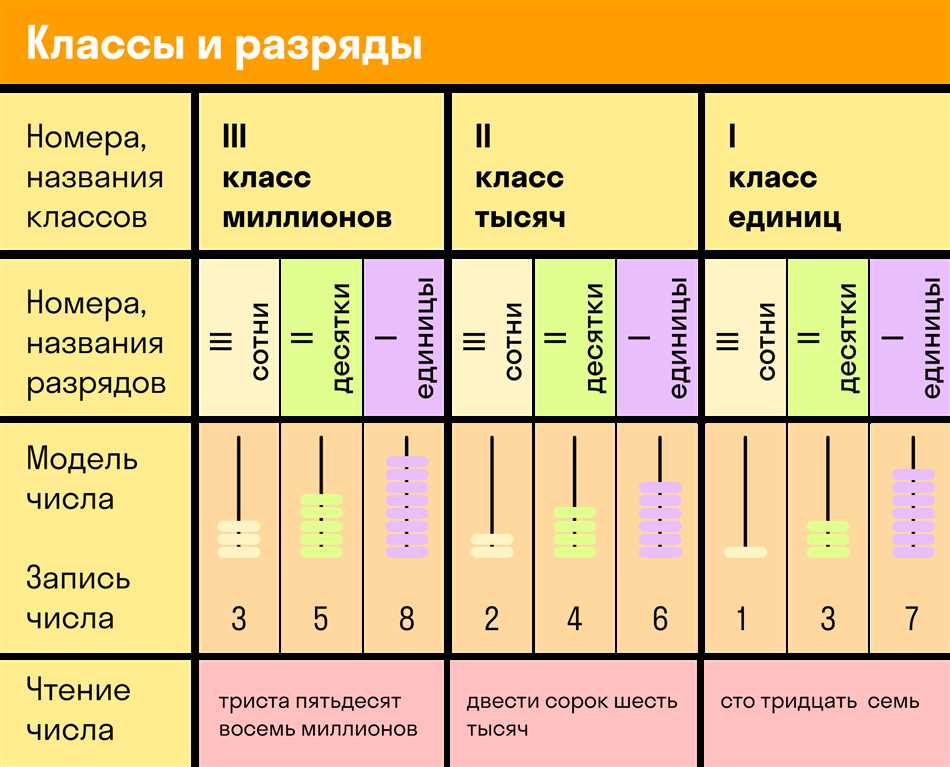
Числа и разряды
Числа окружают нас повсюду — от номеров на дверях до телефонных номеров и цен в магазинах. Зная, как работать с числами, мы можем легко разбираться с этими повседневными ситуациями. Итак, вперед!
Ты наверняка слышал о том, что числа состоят из разрядов. Мы можем представить число в виде суммы разрядов, где каждый разряд имеет свое значение. Для примера возьмем число 5732. В нем есть четыре разряда: тысячи, сотни, десятки и единицы. Число 5 находится в разряде тысяч, 7 — в разряде сотен, 3 — в разряде десятков, а 2 — в разряде единиц.
Каждый разряд имеет свое значение, которое зависит от его положения в числе. Например, в разряде тысяч каждая цифра умножается на 1000, в разряде сотен — на 100, в разряде десятков — на 10, и в разряде единиц — остается без изменений. Таким образом, число 5732 можно представить как (5 * 1000) + (7 * 100) + (3 * 10) + 2.
И вот еще один интересный факт: чем правее находится разряд в числе, тем меньше его значение. Например, разряд единиц имеет самое маленькое значение, а разряды тысяч — самое большое.
Теперь, когда ты разобрался с понятием разрядов и их значений, ты можешь легко работать с числами. Не бойся экспериментировать и практиковаться — только так ты сможешь улучшить свои навыки в математике!
Ну что, каковы твои мысли по поводу чисел и разрядов? Значит, приготовься использовать свои новые знания в повседневной жизни! Удачи тебе, друг, и пусть математика всегда будет на твоей стороне!
Понятие разряда
Но не просто так! Разряды имеют особое значение. Например, в числе 785, цифра 5 занимает место в единицах, цифра 8 занимает место в десятках, а цифра 7 — в сотнях. Каждый разряд представляет значение в зависимости от своего положения.
Давай пройдемся по разрядам:
- Разряд единиц — это самый младший разряд числа. В нем можно найти цифры от 0 до 9.
- Разряд десятков — это следующий разряд после единиц. В нем можно найти цифры от 0 до 9.
- Разряд сотен — это разряд после десятков. Опять же, в нем можно найти цифры от 0 до 9.
И так далее, каждый следующий разряд увеличивается в 10 раз. Например, разряд тысяч содержит значения от 0 до 9, разряд десятков тысяч — от 0 до 9, а разряд сотен тысяч — также от 0 до 9.
Таким образом, понимание разрядов помогает нам распознавать и понимать значения чисел. Они помогают нам решать различные математические задачи, основанные на числах и их разрядах.
Десятичная система счисления

В десятичной системе счисления мы используем десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждая цифра представляет определенное количество, которое зависит от ее позиции в числе.
Давайте посмотрим на пример. Возьмем число 357. В этом числе цифра 7 находится в единичном разряде, цифра 5 — в десятичном разряде, а цифра 3 — в сотенном разряде. Каждая позиция в числе умножается на соответствующую степень числа 10.
Теперь представьте, что вы пишете число 658. Вопрос для вас: какую цифру вы меняете, чтобы получить число, большее 658? Если вы ответили «цифру в сотенном разряде», то вы правильно ответили! Если вы заменили цифру 6 на 7, то получили число 758.
Десятичная система счисления очень важна в нашей жизни. Мы используем ее для счета денег, измерения времени и многих других вещей. Почти все, что мы делаем, связано с числами, и понимание десятичной системы счисления помогает нам лучше понимать мир вокруг нас.
Так что следующий раз, когда вы увидите число, подумайте о том, как оно представлено в десятичной системе счисления. И помните, что числа везде — от счета овечек перед сном до звезд в небе.
Основание числа
Знаешь ли ты, что в мире существует не только десятичная система счисления? В математике есть другие системы, и в каждой из них числа представляются по-разному. Но вне зависимости от системы, есть одна общая вещь, которая называется «основание числа».
Основание числа — это число, которое определяет, сколько «разрядов» может быть в числе. Например, в десятичной системе счисления основание равно 10, поэтому число может быть составлено из десяти разрядов: от 0 до 9. В двоичной системе счисления основание равно 2, поэтому число может быть составлено только из двух разрядов: 0 и 1.
Когда мы записываем число в разных системах счисления, мы используем цифры и позиции, чтобы указать значение каждого разряда. Например, в десятичной системе число 1234 состоит из разрядов с значениями 1, 2, 3 и 4, умноженными на соответствующие степени десяти. В двоичной системе число 1101 представляет собой сумму разрядов с значениями 1, 2 и 8, умноженными на соответствующие степени двойки.
Понимание основания числа поможет тебе лучше понять, как работают разные системы счисления и как записывать числа в них. Так что, почему бы не провести небольшой эксперимент и записать несколько чисел в разных системах счисления? Ты удивишься, насколько весело и интересно это может быть!
Запись чисел в разрядах
Так вот, запись чисел в разрядах — это когда мы разбиваем число на группы и каждая группа имеет свой разряд. Например, давай взглянем на число 357. Мы можем разделить его на группы по три цифры: сотни, десятки и единицы. Теперь можем записать это число как 300 (сотни), 50 (десятки) и 7 (единицы).
Что интересно в записи чисел в разрядах, так это то, что мы можем использовать это понятие для больших чисел. Вместо того, чтобы записывать число 20345, мы можем разбить его на группы и записать его как 20 (тысячи), 300 (сотни), 40 (десятки) и 5 (единицы).
Запись чисел в разрядах помогает нам понять структуру числа и работать с ним более удобно. Например, мы можем легко складывать и вычитать числа, зная, что каждый разряд имеет свою весовую ценность.
Надеюсь, теперь ты лучше понимаешь, что такое запись чисел в разрядах. Она помогает нам разобраться с большими числами и работать с ними без проблем. Давай экспериментировать с числами и применять эти знания на практике!
Перевод чисел из одной системы счисления в другую
Давай начнем с основных систем счисления: десятичной, двоичной и шестнадцатеричной. В десятичной системе мы используем цифры от 0 до 9, в двоичной — только 0 и 1, а в шестнадцатеричной — от 0 до 9 и буквы от A до F.
Чтобы перевести число из одной системы счисления в другую, мы используем метод замены разрядов. Например, если у нас есть число 101 в двоичной системе, мы можем перевести его в десятичную систему, заменив разряды согласно формуле: каждую цифру умножаем на соответствующую степень основания системы счисления и складываем все полученные значения. Таким образом, 101 в двоичной системе равно 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 5 в десятичной системе.
Теперь давай посмотрим, как перевести число из десятичной системы в двоичную. Здесь мы будем делить число на 2 и записывать остатки в обратном порядке. Например, если у нас есть число 10 в десятичной системе, мы делим его на 2 и получаем 5 с остатком 0. Далее делим 5 на 2 и получаем 2 с остатком 1. И, наконец, делим 2 на 2 и получаем 1 с остатком 0. Записывая остатки снизу вверх, получаем 1010 в двоичной системе.
А как насчет перевода числа из десятичной системы в шестнадцатеричную? Здесь мы также будем делить число, но уже на 16. Остатки от деления представляем с помощью букв: 10 — A, 11 — B, 12 — C и так далее. Например, если у нас есть число 15 в десятичной системе, мы делим его на 16 и получаем 0 с остатком 15. Остаток 15 представляем как F, итак, 15 в десятичной системе равно F в шестнадцатеричной системе.
Надеюсь, теперь тебе понятно, как переводить числа из одной системы счисления в другую. Это очень полезный навык, который пригодится не только в математике, но и в программировании и других областях. Попрактикуйся в переводе чисел различных систем счисления и стань настоящим мастером в этом деле!
Суммирование чисел в разрядах
Давай рассмотрим, что значит «суммировать числа в разрядах». Когда мы складываем числа, мы смотрим на каждый разряд и суммируем цифры, стоящие на одной позиции. Например, если у нас есть число 456, мы можем разбить его на сумму 400, 50 и 6.
Однако, при сложении сумму каждого разряда нужно вычислять отдельно. Например, если у нас есть два числа: 456 и 327, мы начинаем с суммы цифр в младшем разряде (единицы). Здесь 6+7=13, но мы не можем записать две цифры в одну позицию, поэтому мы записываем 3 в разряд единиц и переносим 1 к следующему разряду.
Затем мы суммируем цифры в следующем разряде (десятки). Здесь 5+2+1 (перенос) = 8, и записываем 8 в разряд десятков.
В конце мы суммируем цифры в старшем разряде (сотни). Здесь 4+3=7, и записываем 7 в разряд сотен.
Чтобы лучше понять этот процесс, давай рассмотрим другой пример: сложение чисел 123 и 456. В этом случае, мы начнем с суммы цифр в разряде единиц: 3+6=9. Затем мы переходим к разряду десятков: 2+5 (перенос 1) = 8. Наконец, мы суммируем цифры в разряде сотен: 1+4 (перенос 0) = 5.
Таким образом, получаем ответ 579.
Умножение и деление чисел в разрядах
Умножение чисел в разрядах
Для умножения чисел в разрядах нам нужно перемножить цифры каждого разряда по очереди. Например, умножим 34 на 12. Сначала умножим 4 на 2, получаем 8. Запишем 8 внизу. Затем умножим 4 на 1, получаем 4. Запишем 4 вверху, но сдвинем его на один разряд влево. Таким образом, получаем 4 внизу и 4 вверху, что дает нам 408. Просто, правда?
Деление чисел в разрядах
Теперь перейдем к делению чисел в разрядах. Здесь нам нужно разделить число с более высоким разрядом на число с более низким разрядом и записать частное. Например, поделим 572 на 4. Начнем с первого разряда. 5 не делится на 4, поэтому идем к следующему разряду. 57 делится на 4 без остатка, поэтому записываем 14 внизу. Затем перемещаемся к следующему разряду и получаем остаток 2. Пишем его внизу, причем сдвигаем на один разряд влево. Итак, получаем частное 143 и остаток 2. Вот и все!
Вот и все, что я хочу сказать на тему умножения и деления чисел в разрядах. Надеюсь, теперь тебе стало понятно, как это делается. Практикуйся и скоро станешь настоящим мастером разрядов!