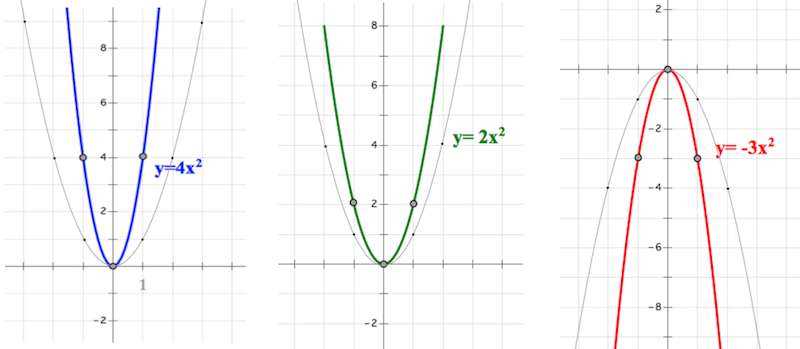
Коэффициент b является одним из важных показателей, определяющих форму и положение параболы. В параболическом уравнении y = ax^2 + bx + c, коэффициент b отвечает за сдвиг параболы по оси x.
Значение коэффициента b указывает, насколько велика горизонтальная составляющая параболы. Если значение b положительно, парабола смещается вправо, а если оно отрицательно, парабола смещается влево. Это связано с тем, что коэффициент b определяет положение вершины параболы.
Кроме того, значением коэффициента b можно контролировать наклон параболы. Если значение b большое, парабола будет иметь более стремительный наклон, а если значение b маленькое, наклон будет более пологим.
Таким образом, коэффициент b играет важную роль в определении формы и положения параболы, а также наклона ее кривой.
Раздел 2: Что представляет собой коэффициент b
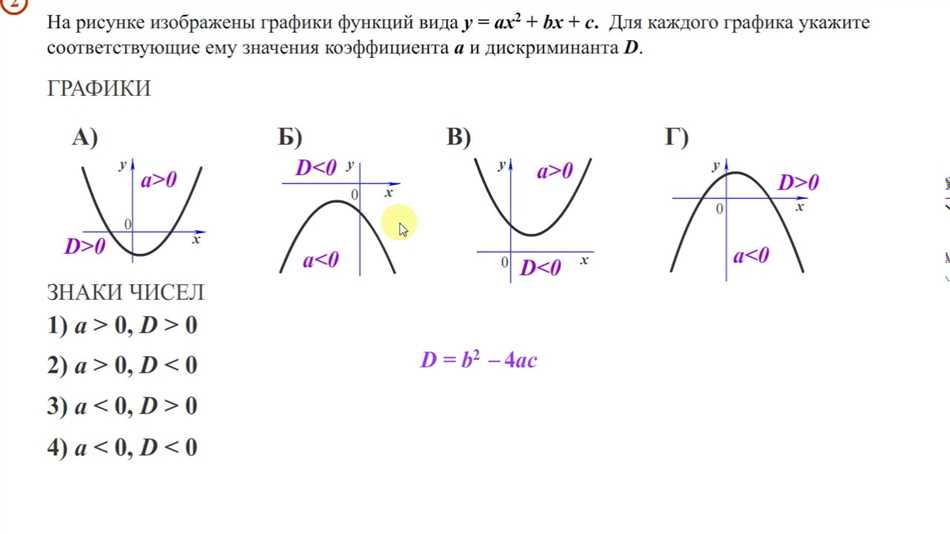
Коэффициент b в параболе отвечает за сдвиг параболы влево или вправо. Если b положительное число, парабола смещается вправо, а если b отрицательное число, парабола смещается влево.
Представьте себе, что вы имеете уравнение параболы вида y = ax^2 + bx + c. Коэффициент b определяет положение параболы на оси x. Если b равно нулю, то парабола будет проходить через ось y и будет отражаться симметрично. Но, как только значение b начинает отличаться от нуля, парабола начинает смещаться.
Давайте посмотрим на примере. У нас есть уравнение параболы y = x^2 + 2x + 1. Здесь b равно 2. Это означает, что парабола смещена вправо на 2 единицы. Если бы у нас было y = x^2 — 2x + 1, то парабола была бы смещена влево на 2 единицы.
Коэффициент b также влияет на наклон параболы. Чем больше значение b, тем более крутая парабола. Если значение b положительное, парабола открывается вверх, а если отрицательное, она открывается вниз.
Рассмотрим еще один пример. У нас есть уравнение параболы y = x^2 + 4x + 4. Здесь b равно 4. Поскольку b положительное число, парабола открывается вверх и имеет более крутой наклон, чем у параболы с меньшим значением b.
Раздел 3: Влияние коэффициента b на форму параболы
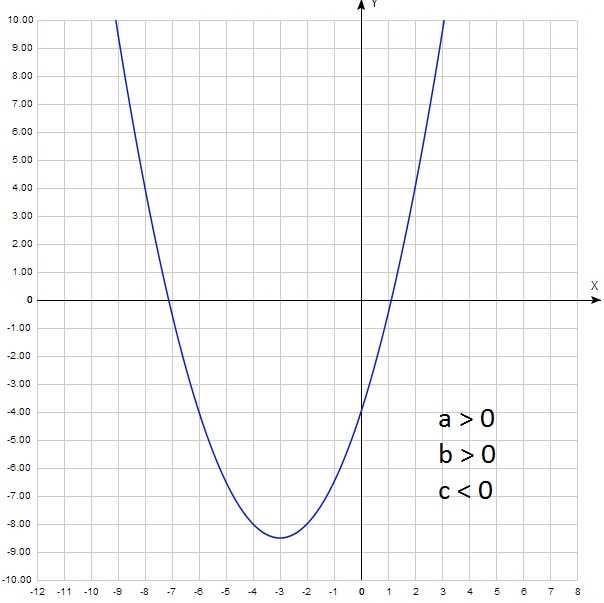
Коэффициент b в уравнении параболы имеет значительное влияние на ее форму и характеристики. Он определяет смещение параболы вверх или вниз и ее направление. Рассмотрим более подробно этот коэффициент и его влияние на форму параболы.
Коэффициент b в уравнении параболы задает смещение параболы вверх или вниз относительно оси ординат. Если b положительный, то парабола смещается вверх, а если b отрицательный, она смещается вниз. Величина смещения зависит от значения b — чем больше абсолютное значение b, тем больше смещение.
Кроме смещения, коэффициент b также определяет направление параболы. Если b положительный, то парабола открывается вверх, а если b отрицательный, она открывается вниз. Направление параболы также зависит от значения b — чем больше абсолютное значение b, тем более открытой или закрытой будет парабола.
Пример 1: Рассмотрим уравнение параболы y = x^2 + 3. Коэффициент b равен 3, что означает, что парабола будет смещена вверх на 3 единицы относительно оси ординат. Она также откроется вверх, создавая впечатление возвышенности.
Пример 2: Теперь рассмотрим уравнение параболы y = x^2 — 2. Коэффициент b равен -2, что означает, что парабола будет смещена вниз на 2 единицы относительно оси ординат. Она также откроется вверх, но будет более закрытой, чем в предыдущем примере.
Коэффициент b также влияет на вершину параболы. Вершина параболы — это точка, в которой парабола достигает своего экстремума или самой высокой/низкой точки на графике. Для параболы вида y = ax^2 + bx + c, координаты вершины можно найти с помощью формулы x = -b/2a и y = f(x), где f(x) — подставление значения x в уравнение параболы.
Вершина параболы скоординатами (h, k) определяет ее положение и форму. Если b положительный, то вершина будет иметь отрицательную координату k, что означает, что парабола откроется вверх и будет расположена ниже оси ординат. Если b отрицательный, то вершина будет иметь положительную координату k, что означает, что парабола откроется вниз и будет расположена выше оси ординат.
Итак, коэффициент b в уравнении параболы играет огромную роль в определении ее формы, смещения, направления и вершины. При изучении парабол и их характеристик важно учитывать значение этого коэффициента и его влияние на график.
Коэффициент b в параболе: его влияние и значение
Значение коэффициента b влияет на положение параболы на координатной плоскости и форму ее графика:
- Если b > 0, парабола смотрит вверх и ее вершина находится выше оси OX.
- Если b < 0, парабола смотрит вниз и ее вершина находится ниже оси OX.
- Если b = 0, парабола параллельна оси OX и ее вершина совпадает с началом координат.
Значение коэффициента b также определяет наклон параболы и скорость ее роста или падения:
- Чем больше модуль значения коэффициента b, тем более крутая парабола и быстрее изменяется ее значение. Например, при b = -2 и b = -4 нижеасимптотическая линия будет идти гораздо быстрее, чем при b = -1.
- При отрицательных значениях коэффициента b парабола будет испытывать увеличение вниз.
- При положительных значениях коэффициента b парабола будет испытывать увеличение вверх.
Таким образом, коэффициент b в параболе играет важную роль при определении ее формы, положения и направления открывания. Подобно другим коэффициентам, его значение может быть изменено, чтобы получить желаемый результат. Он является одним из элементов, определяющих уравнение параболической функции и может быть использован для управления ее поведением на графике.