Ротор в математике: определение и примеры

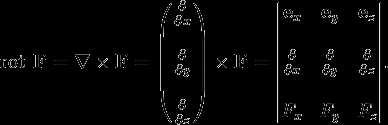
Ротор – это понятие, используемое в векторном анализе для описания вращательных свойств поля. Он позволяет измерить величину и направление кручения или вихревого движения вокруг точки. Ротор определяется как векторная операция, которая применяется к векторному полю и результатом является другое векторное поле. Математически вычисление ротора связано с операцией криволинейного дифференцирования, градиентом и криволинейным интегралом. Важно отметить, что ротор имеет фундаментальное значение в физике, так как позволяет описывать электромагнитные поля и гидродинамические потоки, а также играет важную роль в решении многих других задач, связанных с вращательными явлениями.

Определение ротора

Представь, что у тебя есть поле, которое описывает направление и интенсивность некоторой физической величины, например, скорость жидкости или электрическое поле. Ротор показывает, насколько эти перемены величины в разных точках поля вращаются или изгибаются. Он позволяет нам понять, есть ли в поле вихрь, и если есть, то как сильно и куда он направлен.

Давай посмотрим на пример. Представь, что ты наблюдаешь волну на воде, и это поле описывает скорость движения воды. Если вода вращается вокруг какой-то точки, то поле будет иметь высокий ротор в этой области. Если вода течет равномерно, без изменений, то ротор будет равен нулю.

Очень удобно использовать ротор, когда мы имеем дело с вихревыми структурами, потому что он позволяет нам определить их интенсивность и направление. Мы можем использовать ротор в различных областях, таких как электромагнетизм, гидродинамика и многих других.

Так что вот, ротор — это одна из тех магических операций в математике, которая помогает нам разгадывать тайны вихрей и вращений в нашем мире.

Физический смысл ротора

Вы, наверное, никогда не думали о том, что такое «ротор», когда делали свои домашние задания по математике. Но обнаруживаете ли вы, что многим математическим понятиям можно придать физический смысл?

Итак, что такое ротор в математике? Вот пример, основанный на трехмерном пространстве. Предположим, у вас есть векторное поле, которое можно визуализировать как поток воздуха. Тогда ротор показывает, насколько плотный поток воздуха вращается в каждой точке этого поля.

Можно представить, что каждая точка в поле вызывает вертушку или карусель, и ротор покажет, насколько быстро она вращается. Чем сильнее вращение, тем больше ротор.

Это поле может использоваться во многих различных областях, таких как физика, инженерия и аэродинамика, чтобы понять, как воздух или другие флюиды движутся в пространстве. Знание ротора позволяет нам определить вихревое движение жидкостей и газов, предсказывать паттерны ветра и даже разрабатывать более эффективные системы вентиляции и охлаждения.

Таким образом, физический смысл ротора заключается в том, что он позволяет нам понять и изучать вращательные движения векторных полей и их влияние на окружающую среду.

Применение ротора в различных областях

Ротор, или векторное поле, играет ключевую роль во многих науках и областях, таких как физика, инженерия и математика. Давайте рассмотрим, как ротор применяется в каждой из этих областей.

Физика

В физике ротор часто используется для описания движения жидкостей и газов. Например, он помогает нам понять вращение вихря в жидкости или течение электромагнитного поля в пространстве. Ротор также используется для вычисления магнитных полей и индукции в электромагнитных системах.

Инженерия

В инженерии ротор применяется для анализа и конструирования различных механических систем. Он помогает в расчетах турбин, компрессоров и других механизмов, а также в определении гидродинамического сопротивления при движении тела в жидкости или газе. Также ротор используется для моделирования электрических цепей и оптимизации работы электронных устройств.

Математика

В математике ротор играет важную роль в векторном анализе. Он используется для нахождения дивергенции и градиента векторных полей, а также для решения уравнений Навье-Стокса, описывающих движение жидкостей. Ротор также применяется в теории функций комплексного переменного и в дифференциальной геометрии.

Таким образом, ротор широко применяется в различных областях, помогая нам лучше понять и описывать физические явления, конструировать и анализировать инженерные системы и решать разнообразные математические проблемы. Независимо от того, работаете ли вы в науке, инженерии или математике, понимание ротора может быть незаменимым инструментом для решения сложных задач и создания новых технологий.

Теорема о роторе

Но что же делает теорему о роторе такой особенной? Ну, она говорит нам, что ротор поля скоростей жидкости или газа равен потоку векторного поля через поверхность, ограниченную этим полем. Представьте себе, что вы смотрите на брызги фонтана и пытаетесь понять, как они движутся. Ротор позволяет нам увидеть, как вода вращается и перемещается вокруг фонтана.

Итак, задолго до того, как мы стали использовать ротор в науке и инженерии, он использовался художниками и дизайнерами. Они применяли его, чтобы создавать красивые и изящные движения в своих работах. Например, ротор был ключевым элементом в создании потрясающих кружевных узоров или визуализации водного потока во время рисования реки или океана.

Заключение

В данной статье были рассмотрены примеры вычисления ротора в различных системах координат. Примеры показали, что ротор может быть выражен в виде аналитической формулы, которая зависит от производных компонент векторного поля по соответствующим координатам.

Таким образом, вычисление ротора является полезным инструментом для анализа вихревых структур и вращения векторных полей. Знание методов вычисления ротора позволяет более глубоко понять физические и геометрические свойства векторных полей.