Середина отрезка в геометрии 7 класс — объяснение и примеры

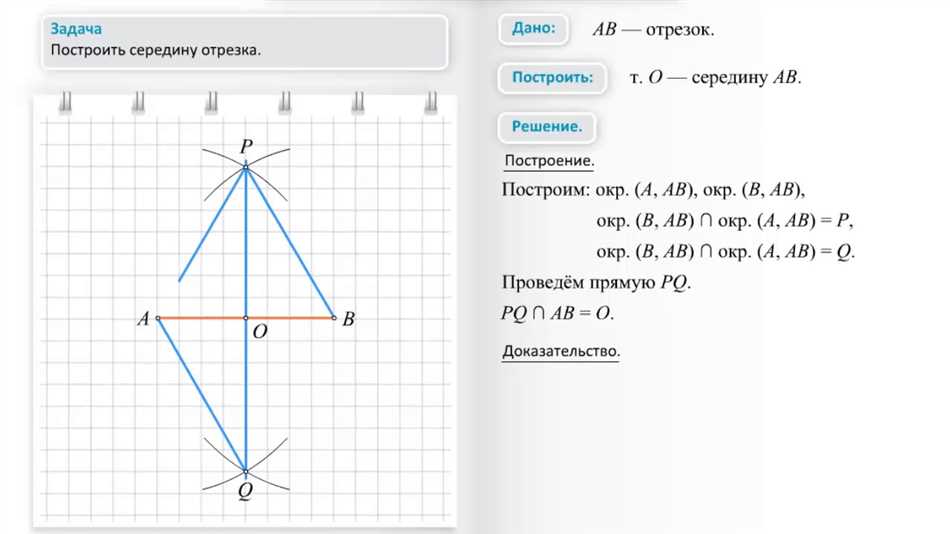
Если мы хотим найти середину отрезка, это значит мы хотим разделить его на две равные части. Середина отрезка находится точно посередине, на равном расстоянии от его концов. Для найдения середины отрезка можно использовать геометрическую конструкцию. Нам понадобится циркуль и линейка. Сначала мы ставим концы отрезка на отметках на линейке, а затем, зажимая циркуль за ножку, делаем окружность с таким радиусом, чтобы она пересекла отрезок в двух точках. Точка пересечения окружности с отрезком будет являться серединой этого отрезка. Важно помнить, что середина отрезка не зависит от его длины, и всегда находится посередине.

Середина отрезка в геометрии 7 класс

Допустим, у нас есть отрезок AB. Серединой этого отрезка называется точка, которая находится на равном расстоянии от точки A и точки B. Другими словами, если мы измерим расстояние от точки A до середины отрезка и расстояние от точки B до середины отрезка, то получим одинаковые значения.

Но как найти середину отрезка? Не переживай, это довольно просто. Можно использовать теорему о середине отрезка, которая гласит: середина отрезка является точкой пересечения его диагоналей.

А что такое диагонали? Это прямые линии, которые соединяют противоположные углы фигуры. Например, если у нас есть прямоугольник ABCD, то диагонали будут отрезками AC и BD. Таким образом, середина отрезка AC будет точкой пересечения диагоналей прямоугольника ABCD.

Надеюсь, я смог помочь тебе понять, что такое середина отрезка в геометрии. Это очень полезное понятие, с помощью которого можно решать задачи и доказывать теоремы. Удачи в изучении геометрии!

Определение середины отрезка

Давай представим, что у тебя есть отрезок на листе бумаги. Одним концом он крепится в одной точке, а другим в другой. Чтобы найти середину этого отрезка, ты можешь провести линию или линию с подписью от начальной точки до конечной. Затем, чтобы найти середину, тебе нужно измерить расстояние от начальной точки до середины, а затем измерить это же расстояние от середины до конечной точки. Если оба измерения одинаковы, то ты нашел середину отрезка!

Зачем нам нужно знать, как найти середину отрезка? Ну, это может быть полезно, когда нам нужно разделить что-то на две равные части, например, кусок торта или отрезок трубопровода. Кроме того, понимание середины отрезка помогает нам также понять и решать другие геометрические задачи, связанные с отрезками и их свойствами.

Координаты середины отрезка

Чтобы найти координаты середины отрезка, нам понадобятся координаты начальной и конечной точек. Представьте себе, что отрезок лежит на числовой прямой. Если у нас есть отрезок AB, где А имеет координату (x1, y1), а В имеет координату (x2, y2), то координаты середины отрезка можно найти следующим образом:

• Для линии X: координата середины будет равна (x1 + x2) / 2
• Для линии Y: координата середины будет равна (y1 + y2) / 2

Получив эти значения, мы найдем координаты середины отрезка. Просто сложите координаты начальной и конечной точек по каждой оси и разделите результат на 2.

Теперь, когда вы знаете, как найти координаты середины отрезка, вы сможете справиться с любыми задачами, связанными с этой темой. Удачи в ваших геометрических приключениях!

Свойства середины отрезка

• Расстояние от начала отрезка до середины равно расстоянию от середины до конца. Это свойство помогает нам понять, что середина отрезка находится на равном удалении от начала и конца.
• Середина отрезка делит его на две равные части. Если мы берем линейку и измеряем расстояние от начала до середины, оно будет равно расстоянию от середины до конца.
• Середина отрезка лежит на прямой, соединяющей начало и конец отрезка. Это значит, что если мы проведем прямую линию через начало, середину и конец отрезка, она будет проходить через середину.

Интересно, правда? Теперь, когда мы знаем эти свойства, мы можем использовать их в геометрии, чтобы решать задачи и находить нужные точки на отрезках. Например, мы можем использовать середину отрезка, чтобы найти другую точку, расположенную на определенном расстоянии от начала или конца отрезка.

Перпендикуляр из середины отрезка

Теперь, представь, что у нас есть отрезок AB, и мы знаем его середину C. Мы можем провести прямую линию, которая будет перпендикулярна к отрезку AB и будет проходить через его середину C. Это называется перпендикуляр из середины отрезка.

Зачем это нужно? Ну, это один из способов нахождения середины отрезка, если мы знаем начальную и конечную точку. А еще это очень полезно в геометрии, когда мы исследуем фигуры, строим построения и решаем задачи. И помни, геометрия — это интересно и полезно, она помогает нам лучше понять мир вокруг нас!

Секущая из середины отрезка

Тебе когда-нибудь приходилось задумываться о том, что произойдет, если из середины отрезка провести линию, которая пересекает этот отрезок? В таких случаях говорят о секущей из середины отрезка. Интересно, не так ли?

Секущая – это линия, которая пересекает отрезок. Если провести секущую из середины отрезка, она разделит отрезок на две равные части. То есть, если отрезок имеет точку A на одном конце и точку B на другом конце, то секущая из середины будет проходить через точку, являющуюся серединой отрезка, и пересекать его в этой точке.

Секущая из середины отрезка имеет много применений в геометрии. Она помогает в построении перпендикуляров, а также может использоваться в задачах о нахождении площади фигур.

Теперь, когда ты знаешь, что такое секущая из середины отрезка, можешь использовать это знание в своих геометрических задачах и построениях. Поехали!

Примеры решения задач про середину отрезка

Давайте рассмотрим несколько примеров задач, которые связаны с определением и свойствами середины отрезка.

Пример 1:

У нас есть отрезок AB длиной 10 см. Найдите координаты точки M, являющейся серединой отрезка AB.

Решение:

Для нахождения координат точки M, мы можем использовать формулы нахождения среднего значения для координат. Если координаты точки A равны (x1, y1), а координаты точки B равны (x2, y2), то координаты середины отрезка M будут:

• x_M = (x₁ + x₂) / 2
• y_M = (y₁ + y₂) / 2

В этом случае, если точка A имеет координаты (2, 4), а точка B имеет координаты (8, 6), то координаты точки M будут:

• x_M = (2 + / 2 = 5
• y_M = (4 + 6) / 2 = 5

Таким образом, точка M имеет координаты (5, 5).

Пример 2:

У вас есть треугольник ABC, и вы знаете, что точка M является серединой стороны AB. Найдите отношение длины стороны AM к длине стороны BM.

Решение:

По свойству середины отрезка, значение отношения длины стороны AM к длине стороны BM равно 1:1. То есть, AM = BM. Это означает, что отрезок AM равен отрезку BM в данном треугольнике.

Пример 3:

Дано, что точка P является серединой отрезка CD. Точка A имеет координаты (8, 2), а точка B имеет координаты (4, 6). Найдите координаты точки D.

Решение:

Если точка P является серединой отрезка CD, то сумма координат точек C и D будет равна удвоенным значениям координат точки P.

В данном случае, если точка P имеет координаты (x_P, y_P), то координаты точки D будут:

• x_D = 2 * x_P — x_A = 2 * x_P — 8
• y_D = 2 * y_P — y_A = 2 * y_P — 2

Таким образом, если точка P имеет координаты (6, 4), то координаты точки D будут:

• x_D = 2 * 6 — 8 = 4
• y_D = 2 * 4 — 2 = 6

Таким образом, координаты точки D равны (4, 6).

Такие задачи помогают нам понять и применить свойства середины отрезка. Они позволяют нам увидеть практическое значение и применение этого понятия в геометрии.

Использование середины отрезка в реальной жизни

Первое применение середины отрезка можно увидеть в конструкции мостов и зданий. Инженеры используют середину отрезка для вычисления равномерно распределенной нагрузки и определения точки подвеса или опоры. Знание середины отрезка помогает создавать устойчивые и прочные конструкции.

Кроме того, середина отрезка применяется в медицине. Например, при введении инъекции, врачи стараются выбирать точку, расположенную близко к середине отрезка. Это обеспечивает более равномерное распределение лекарственного вещества и снижение возможных побочных эффектов.

Также середина отрезка может быть использована в навигации. При определении координат и маршрутов, географы учитывают принцип середины отрезка для более точного определения местоположения объектов и планирования пути.

В целом, использование середины отрезка в реальной жизни помогает рационально использовать ресурсы и обеспечивать эффективность в различных областях, от строительства до медицины и навигации.