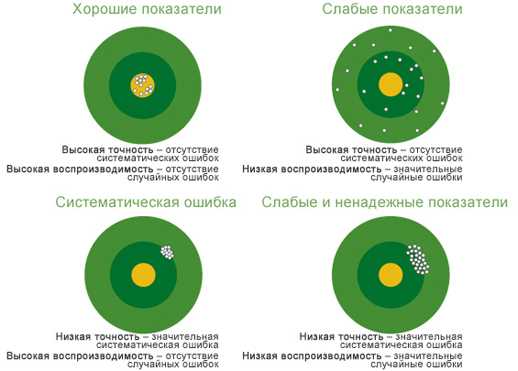
Определение сходимости
В математике сходимость относится к понятию, когда элементы последовательности или значения функции приближаются к определенному значению или пределу. Сходимость позволяет нам определить, насколько близко последовательность или функция приближаются к своему предельному значению, и как быстро они стремятся к этому значению.
Сходимость может быть представлена математически с использованием различных понятий, таких как предел последовательности, предел функции, предел по мере, точечная сходимость и др. Каждое из этих понятий имеет свои собственные определения и критерии для описания сходимости.
В целом, сходимость является основополагающим понятием во многих областях науки и математики. Она позволяет нам описывать и изучать поведение систем и процессов, обеспечивает точность и надежность результатов измерений и экспериментов, и способствует развитию науки и технологии.
Факторы, влияющие на сходимость результатов измерений
Влияние на сходимость результатов измерений оказывают различные факторы, среди которых можно выделить следующие:
- Качество и точность используемых измерительных приборов: одним из основных факторов, влияющих на сходимость результатов, является качество и точность измерительных приборов. Использование неправильных или неисправных приборов может привести к неточным результатам. Поэтому необходимо выбирать и использовать приборы с высокой точностью и надежностью, а также регулярно проверять их работоспособность.
- Квалификация и опытность оператора: роль оператора измерений также велика. Некомпетентность или неопытность оператора может привести к ошибкам при выполнении измерений. Поэтому необходимо уделять особое внимание обучению и тренировке операторов, чтобы они имели достаточную квалификацию и опыт для проведения измерений.
- Условия окружающей среды: окружающая среда и условия, в которых проводятся измерения, также оказывают влияние на сходимость результатов. Факторами, которые могут повлиять на измерения, являются температура, влажность, электромагнитные помехи и другие. Поэтому необходимо обеспечить оптимальные условия для проведения измерений, например, изолировать приборы от внешних помех или поддерживать стабильную температуру.
- Методика измерений: правильный подход и методика измерений также важны для получения сходимых результатов. Неправильная методика может привести к искажению данных и неточным результатам. Поэтому необходимо разработать и применять правильные методики, которые учитывают особенности измеряемого объекта и учитывают все факторы, которые могут повлиять на результаты измерений.
- Стандартные образцы и калибровка: использование стандартных образцов и калибровка измерительных приборов также играют важную роль в сходимости результатов. Стандартные образцы позволяют проверить и калибровать приборы, а калибровка позволяет установить точность измерений. Поэтому необходимо регулярно проводить проверку и калибровку приборов, а также использовать стандартные образцы для сравнения и контроля.
Все эти факторы оказывают влияние на сходимость результатов измерений и, следовательно, на надежность и точность полученных данных. Учитывая все эти факторы и применяя соответствующие методики, можно достичь высокой сходимости результатов измерений и повысить надежность и точность получаемой информации.
Методы оценки сходимости
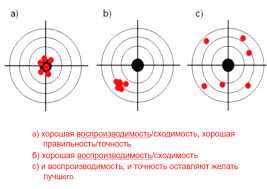
Существует несколько методов оценки сходимости, которые широко используются в различных научных дисциплинах:
- Метод последовательных приближений
- Метод регуляризации
- Метод разложения в ряд
- Метод статистических оценок
Метод последовательных приближений основан на итерационном подходе. Он заключается в том, что начиная с некоторого начального значения, производится последовательность приближений, каждое из которых ближе к истинному значению. Этот метод широко применяется в математике и физике для решения различных уравнений и задач.
Метод регуляризации используется для решения проблемы неустойчивости или плохо обусловленных задач. Он заключается в добавлении некоторого регуляризующего параметра в математическую модель, чтобы избежать осцилляций или неустойчивости. Этот метод часто применяется в обработке сигналов, обратной задаче и других областях науки.
Метод разложения в ряд используется для приближенного вычисления функций или решения уравнений. Он заключается в разложении функции или решения в бесконечную сумму или произведение других функций с известными свойствами. Такой подход позволяет получить приближенное решение с любой заданной точностью. Этот метод широко используется в математическом анализе, физике и других научных областях.
Метод статистических оценок является одним из главных инструментов в статистике и экспериментальном исследовании. Он основан на анализе данных и их статистической обработке. Статистические оценки используются для определения точности и надежности измерений, оценки параметров модели, проверки гипотез и других задач статистического анализа.
Выбор метода оценки сходимости зависит от конкретной задачи, типа данных и требуемого уровня точности. Каждый из этих методов имеет свои преимущества и ограничения, поэтому важно выбрать наиболее подходящий метод для конкретной ситуации.
Независимо от выбранного метода, важно проводить анализ погрешности и невязки для оценки сходимости. Это позволяет определить, насколько точно результаты измерений сходятся к истинному значению и принять соответствующие меры для улучшения качества и достоверности результатов.
Практическое применение сходимости и воспроизводимости
Разберемся, что такое сходимость и воспроизводимость, и как они применяются на практике. Сходимость означает, что результаты измерений или экспериментов стремятся к некоторому значению с учетом погрешности. Воспроизводимость, в свою очередь, говорит о том, насколько успешно можно повторить измерения или эксперимент и получить схожие результаты.
Одним из примеров практического применения сходимости и воспроизводимости является медицинская диагностика. Для определения заболеваний и состояния пациента необходимо проводить различные исследования, такие как анализ крови, рентгенография и другие. Важно, чтобы результаты этих исследований были сходными и повторяемыми, чтобы медицинский персонал мог доверять им и принимать обоснованные решения.
В промышленной области, сходимость и воспроизводимость также являются критическими при проведении качественного контроля продукции. Например, в процессе производства автомобилей проводятся множество измерений и испытаний для того, чтобы убедиться, что каждый автомобиль соответствует определенным стандартам и требованиям безопасности.
Также сходимость и воспроизводимость применяются в физике и математике. Многие физические и математические теории базируются на экспериментальных данных, которые должны быть сходными и повторяемыми для подтверждения теорий. Например, в физике элементарных частиц проводятся эксперименты в больших коллайдерах, чтобы обнаружить новые частицы и проверить существующие теории.
Сходимость и воспроизводимость также играют важную роль в научных исследованиях. Ученые проводят эксперименты и измерения, чтобы получить новые знания и улучшить уже существующую науку. Но для того, чтобы результаты исследования были действительно значимыми, необходимо, чтобы они были сходимыми и воспроизводимыми.
Сходимость и воспроизводимость результатов измерения: понятие и применение

Сходимость результатов измерения означает, что при повторении измерений в разных условиях все результаты стремятся к одному и тому же значению или диапазону значений. Если результаты сходятся, то это говорит о надежности и точности проведенных измерений.
Воспроизводимость результатов измерения означает, что другие исследователи могут повторить проведенные измерения и получить сходные результаты. Это позволяет проверить достоверность полученных данных и подтвердить или опровергнуть научные или технические гипотезы.
Сходимость и воспроизводимость результатов измерения имеют большое значение во многих областях науки и техники. Они используются при разработке новых материалов, технологий, медицинских препаратов, клинических исследований и других областях, где точные результаты измерений необходимы для принятия важных решений и разработки новых продуктов.
- Сходимость и воспроизводимость позволяют установить является ли измерение достоверным и точным.
- Сходимость и воспроизводимость помогают валидировать результаты исследования.
- Сходимость и воспроизводимость обеспечивают повторяемость экспериментов.
- Сходимость и воспроизводимость являются основой для проведения статистического анализа.
Для оценки сходимости и воспроизводимости результатов измерения используются различные методы статистического анализа, такие как среднее значение, стандартное отклонение, коэффициент вариации и другие. Эти методы позволяют оценить степень точности и надежности проведенных измерений и определить их пригодность для дальнейшей обработки данных.
| Метод | Описание |
|---|---|
| Среднее значение | Сумма всех измерений, деленная на их количество, показывает центральную тенденцию данных. |
| Стандартное отклонение | Мера разброса данных относительно их среднего значения. |
| Коэффициент вариации | Соотношение стандартного отклонения к среднему значению, выраженное в процентах, позволяет оценить относительную вариабельность данных. |
Таким образом, сходимость и воспроизводимость результатов измерения играют важную роль в науке и технике, обеспечивая достоверность и точность полученных данных. Они позволяют принимать обоснованные решения на основе проведенных исследований и дальнейшей обработки данных.

