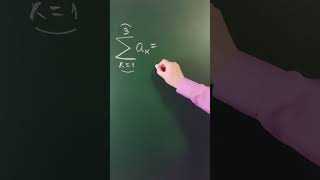
Сигма (символ «Σ») – это математический символ, который часто используется в различных областях науки и инженерии. Он обозначает сумму последовательности чисел или выражений. Значение этого символа в математике заключается в том, что он позволяет удобно записывать сложные выражения, которые требуют постоянной суммирования.
Использование сигма математики требует понимания базовых принципов математической нотации и умения применять его в решении задач. Это позволяет упростить и ускорить процесс анализа информации и повысить точность результатов.
Что такое сигма математика?

Символ сигмы был введен в XVII веке математиком Йозефом Луинхолдом и с тех пор стал неотъемлемой частью математической нотации. Он используется для обозначения суммы всех чисел в заданном ряду. Например, сумма чисел от 1 до 10 может быть записана как ∑(n = 1 до 10) n.
Сигма математика предоставляет удобный и компактный способ записи и обозначения суммы ряда чисел. Она позволяет сократить длинные и трудоемкие выражения, делая их более удобочитаемыми и легкими для понимания. Это особенно полезно при работе с большими наборами данных или при решении сложных математических проблем.
С использованием сигма математики можно решать разнообразные задачи, такие как вычисление суммы арифметической или геометрической прогрессии, нахождение среднего значения ряда чисел или суммы квадратов чисел. Она также широко применяется в других областях науки, включая физику, статистику, экономику и инженерию.
Сигма математика представляет собой мощный инструмент для работы с суммами и рядами чисел. Она упрощает обозначение и вычисление сложных математических операций, а также позволяет сократить объем работы и время выполнения задач. Понимание и применение сигма математики может значительно облегчить математические вычисления и улучшить понимание различных математических концепций.
Значение и основные принципы сигма математики
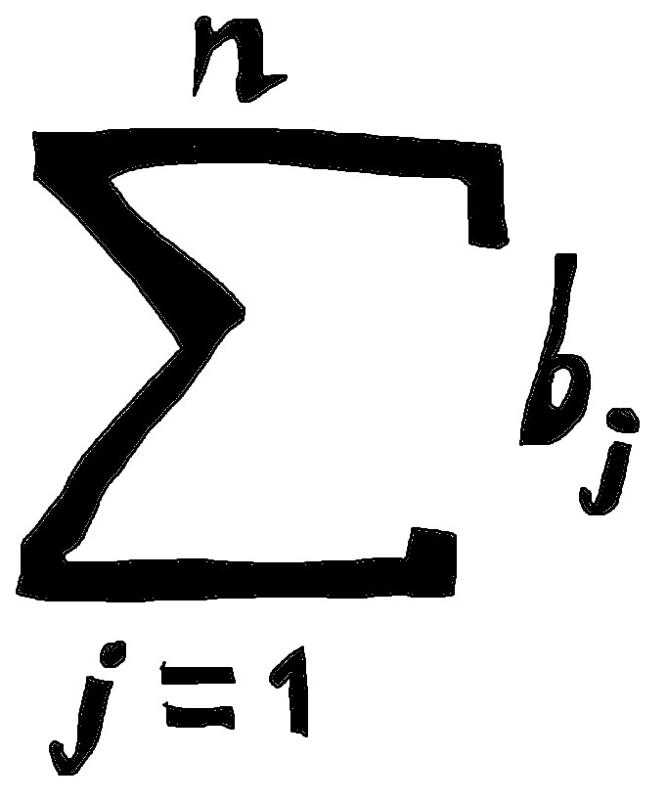
Сигма математика, также известная как сигма-алгебра, является разделом математики, который изучает свойства множеств и операций над ними. Она играет важную роль во многих областях науки, техники и экономики, позволяя анализировать и описывать сложные системы и явления.
Основной принцип сигма математики заключается в использовании символа сигма (∑), обозначающего сумму, для сжатия и упрощения математических выражений. Вместо того чтобы перечислять все элементы множества и складывать их поочередно, мы можем применить сигму-оператор для вычисления суммы всех элементов с помощью более компактной записи.
Кроме того, сигма математика также основывается на принципе индукции — методе математического доказательства, который позволяет нам обобщать утверждения на всю бесконечность, исходя из их верности для некоторых начальных условий. Это позволяет нам решать сложные задачи, которые включают бесконечные множества или последовательности чисел.
Значение сигма математики не ограничивается только академической областью. Она широко используется в физике, инженерии, экономике, информатике и других областях. Например, с ее помощью можно анализировать ряды данных, моделировать сложные системы, оптимизировать процессы и многое другое.
Также сигма математика играет важную роль в обработке и интерпретации статистических данных. Например, ее можно использовать для вычисления среднего значения, дисперсии или суммы определенной выборки. Это принципиально важно для многих исследований и аналитических задач, которые требуют обработки больших объемов данных.
Таким образом, сигма математика имеет огромное значение в современном мире. Она помогает нам лучше понимать и анализировать различные явления и системы, упрощает математические вычисления и способствует развитию науки и технологий. Возможно, вы тоже встречались с сигма-оператором в своем образовании или работе?
Применение сигма математики в науке
Применение сигма математики в науке неограничено и включает в себя различные области знания. Например, в физике суммирование может использоваться для расчета траекторий движения частиц, определения энергетических уровней или анализа экспериментальных данных. В биологии суммирование может применяться для вычисления генетических вероятностей или анализа статистических данных. В экономике суммирование может помочь в анализе доходов и расходов, моделировании финансовых рынков или прогнозировании трендов.
Также сигма математика широко используется в статистике. Суммирование может быть полезным для вычисления средних значений, стандартных отклонений или других характеристик распределений данных. В социальных науках суммирование может помочь в анализе опросных данных, вычислении социологических показателей или изучении общественных тенденций.
Примеры применения сигма математики в науке:

- Расчет суммы прогрессии: S = 1 + 2 + 3 + … + n
- Апроксимация интеграла: ∫f(x)dx ≈ ∑f(x)Δx, где Δx — малый шаг интегрирования
- Вычисление среднего значения: average = 1/n ∑x
- Вычисление стандартного отклонения: σ = √(1/n ∑(x — average)^2)
С помощью сигма математики ученые могут компактно записывать и анализировать большие объемы данных. Это особенно важно в современной науке, где собираются огромные массивы данных, например в генетике или астрофизике.
Применение сигма математики в финансовой аналитике

Что такое сигма математика?
Сигма математика — это статистический инструмент, используемый для измерения разброса данных. Она позволяет определить, насколько удалены данные от среднего значения, и измерить вероятность нахождения данных в определенном диапазоне.
Как используется сигма математика в финансовой аналитике?
В финансовой аналитике сигма математика используется для анализа финансовых данных и оценки рисков. Например, с помощью сигма математики можно определить, как вероятно получить доходность от определенного инвестиционного портфеля или решить, насколько близко находятся фактические результаты компании к ее прогнозным показателям.
Сигма математика также используется для выявления выбросов в данных и оценки стабильности финансовых показателей. Это помогает финансовым аналитикам принимать обоснованные решения, основанные на надежной статистической информации.
Кроме того, сигма математика может быть использована для определения оптимальных уровней риска и доходности в инвестиционной стратегии. Она позволяет определить, какие уровни и распределение риска будут наиболее подходящими для конкретного инвестора или компании.
Интересно, что в финансовой аналитике сигма математика может быть применена как на микроуровне (например, при анализе финансовых показателей отдельной компании), так и на макроуровне (например, при анализе экономических показателей страны).
Преимущества использования сигма математики в финансовой аналитике
- Позволяет определить риски и прогнозировать будущие результаты с высокой точностью;
- Упрощает процесс принятия решений на основе объективных данных;
- Позволяет выявить выбросы и аномалии в данных;
- Способствует оптимизации инвестиционных стратегий и уровней риска;
- Повышает надежность и достоверность финансовых анализов.
Сигма в математике: значение и применение
Использование символа Сигма в математике позволяет компактно и ясно записывать сложные суммы. Он позволяет указать начальное и конечное значение переменной и выразить сумму всех промежуточных значений этой переменной. Например, символ Сигма может быть использован для записи суммы первых n членов арифметической или геометрической прогрессии.
Для использования символа Сигма в математических выражениях следует в качестве аргументов указывать начальное и конечное значение переменной, а также выражение, которое нужно суммировать. Под знаком Сигма могут находиться как простые числа или переменные, так и более сложные формулы или функции.
Применение символа Сигма не ограничивается только математикой. Он также находит применение в физике, статистике, программировании и других науках. В этих областях символ Сигма используется для записи суммирования больших объемов данных или результатов эксперимента. Он помогает сократить объем записи и сделать формулы более понятными и лаконичными.