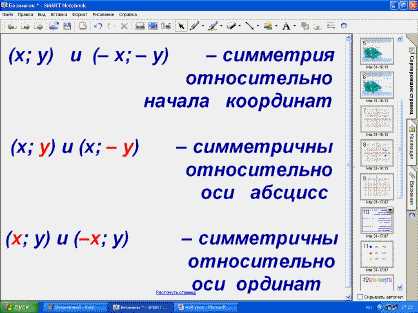
Симметрия относительно начала координат — это особый вид симметрии, который обозначает, что фигура или объект, проходит через точку (0, 0) на координатной плоскости, сохраняя свою форму и размеры. Такая симметрия значит, что если мы отразим фигуру относительно начала координат, получится идентичная копия фигуры.
Примеры фигур с симметрией относительно начала координат включают в себя: круг, эллипс, равносторонний треугольник и множество других геометрических фигур. Если на графике координатной плоскости задана фигура, то для определения симметрии относительно начала координат необходимо проверить, совпадают ли точки фигуры с их отображениями относительно начала координат.
Симметрия относительно начала координат имеет множество практических применений, от создания красивых и симметричных изображений на графике до различных физических и математических моделей. Это важный концепт в изучении геометрии и алгебры, который позволяет анализировать форму и структуру объектов на координатной плоскости.
Зачем нужна симметрия относительно начала координат
Когда мы говорим о симметрии относительно начала координат, мы имеем в виду, что объекты или графики отражаются симметрично относительно оси координат. Это понятие не только математическое, но также применяется в различных областях, таких как физика, графический дизайн и даже в нашей повседневной жизни.
Симметрия относительно начала координат играет важную роль в анализе и представлении графиков и функций. Она помогает нам понять, как изменения в значениях на одной стороне оси влияют на значения на другой стороне. Например, если мы имеем симметричную фигуру относительно начала координат, то мы можем сразу же узнать, что значения на одной стороне будут точно такими же, как на противоположной стороне. Это упрощает анализ и решение математических и физических задач.
Кроме того, симметрия относительно начала координат также является важным аспектом в графическом дизайне. Она помогает создавать сбалансированные и эстетически приятные композиции, привлекая внимание к центральному элементу или оси. Мы можем использовать симметрию, чтобы создать гармонию и порядок в дизайне, что делает его более привлекательным для глаз.
В конечном итоге, симметрия относительно начала координат помогает нам понять и анализировать мир вокруг нас, а также создавать красивые и уравновешенные композиции в графическом дизайне. Она является важным инструментом для решения задач и передачи информации, и без нее многие из наших научных и художественных достижений были бы невозможными.
Принципы симметрии
Один из примеров симметрии — симметрия относительно начала координат. Это означает, что фигура симметрична относительно оси, проходящей через начало координат. Если мы возьмем отражение фигуры относительно этой оси, она будет выглядеть идентично первоначальной фигуре.
Принципы симметрии помогают нам понять и описать мир вокруг нас. Они помогают нам распознавать и создавать гармоничные и эстетически приятные композиции. Например, симметричные формы в архитектуре и дизайне могут придать зданию или предмету привлекательность и сбалансированность.
Так же симметрия может быть полезна в науке и математике. Она позволяет исследовать и анализировать сложные системы и отношения. Математики используют симметрию для понимания структуры и связей между различными объектами.
Подводя итог, принципы симметрии являются универсальными и важными в нашей жизни. Они помогают нам видеть и создавать гармонию, а также понимать и изучать окружающий мир. Стоит задуматься о симметрии и ее роли в нашей жизни.
Определение симметрии относительно начала координат
Другими словами, если мы возьмем фигуру, нарисованную на графике, и отразим ее по отношению к началу координат, то получим идентичную фигуру. Например, если мы нарисуем линию, и она будет симметрична относительно начала координат, то линия будет выглядеть одинаково с обоих сторон.
Симметрия относительно начала координат является особым случаем симметрии относительно оси координат. В этом случае, фигура полностью совпадает с ее отражением и не изменяется при отражении.
Симметрия относительно начала координат встречается в различных областях математики, физики и геометрии. Она имеет важное значение при изучении симметричных графиков функций и решении геометрических задач.
Примеры симметрии относительно начала координат
-
График функции y = x – прямая линия, которая проходит через начало координат и имеет угол наклона 45 градусов. Она является симметричной относительно начала координат, так как отображение ее отражением относительно начала координат не изменяет форму прямой.
-
Окружность – геометрическая фигура, все точки которой равноудалены от центра. Если центр окружности расположен в начале координат, то она будет симметричной относительно начала координат. Если отразить половину окружности относительно начала координат, получится другая половина, и окружность останется неизменной.
-
График функции y = -x^2 – парабола, симметричная относительно начала координат. Отражение половины параболы относительно начала координат даст другую половину, и парабола сохранит свою форму.
Таким образом, симметрия относительно начала координат является важным понятием в математике и геометрии, и часто встречается в различных графиках и фигурах.
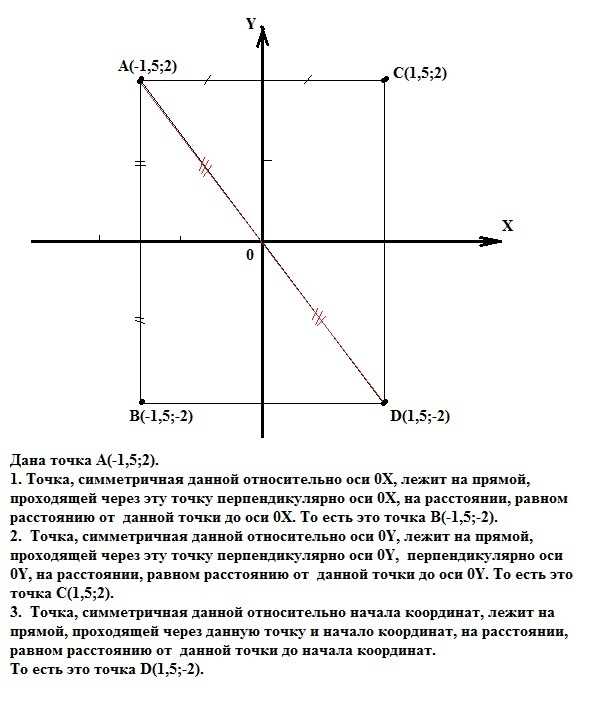
Геометрическое представление симметрии относительно начала координат
Представь, что у тебя есть точка в первом квадранте, координаты которой (2,3). Если ты отразишь эту точку относительно начала координат, новые координаты будут (-2,-3). То же самое произойдет, если отразить точку, находящуюся во втором, третьем или четвертом квадранте.
Итак, симметрия относительно начала координат очень простая и понятная концепция в геометрии. Так как у нас нет ограничений, связанных с положением центра симметрии, мы можем легко определить, является ли фигура симметричной относительно начала координат. Это даёт нам большую свободу в анализе и построении фигур.
Заключение
В физике симметрия относительно начала координат может быть использована, например, для описания движения тела в пространстве. В технических науках симметрия относительно начала координат может быть использована при проектировании симметричных систем, таких как электрические схемы или механические конструкции.
Для математиков симметрия относительно начала координат является исследуемым объектом сама по себе. С помощью этого свойства математики могут решать сложные задачи, исследовать структуру математических объектов и находить новые связи между различными разделами математики.




