Симметрия отрезка является одним из важных понятий в геометрии. Она описывает свойство отрезка быть равным самому себе при отражении относительно какой-то оси. Представь, что ты разметил отрезок на бумаге и его зеркальное отражение поставил рядом. Если они идеально совпали, значит, отрезок обладает симметрией.
Симметрию можно наблюдать не только в геометрии, но и в повседневной жизни. Например, крылья бабочки симметричны, а лицо человека также имеет симметричную структуру. Это свойство придает отрезкам, предметам или формам гармоничный и эстетичный вид.
Симметрия отрезка помогает нам анализировать и понимать геометрические объекты. Некоторые симметричные формы, такие как круги, квадраты или треугольники, используются в дизайне, архитектуре и искусстве для создания баланса и привлекательности.
Симметрия отрезка
А ты знаешь, что такое симметрия? Конечно, ты знаешь! Мы видим ее вокруг нас каждый день. Как, например, в симметричном лице человека или в симметричных крыльях бабочки. Это такое свойство, когда у объекта есть ось, относительно которой он выглядит одинаково с обеих сторон.
Теперь представь себе отрезок. Небольшую линию между двумя точками. А теперь давай поищем ось симметрии. Отрезок, по определению, имеет две конечные точки. Для того, чтобы он был симметричным, остальная часть его должна быть зеркальным отражением этих точек. То есть, если мы возьмем середину отрезка, то от каждой конечной точки до середины мы получим одинаковые отрезки.
Интересно, правда? Вот и я так подумал! Симметрия отрезка — это такое волшебное свойство, которое делает его и визуально привлекательным, и математически интересным. А еще симметричные отрезки используются в архитектуре, дизайне и искусстве. Ведь они могут создать баланс и гармонию в любом проекте.
Свойства симметрии отрезка
Одно из главных свойств симметрии отрезка — симметрия относительно середины. Знаешь, в любом отрезке есть точка, которая делит его пополам. И когда отрезок симметричен относительно этой точки, он равномерно и красиво располагается в пространстве.
Еще одно замечательное свойство — симметрия относительно оси. Представь себе отрезок, который лежит на прямой линии. Если этот отрезок симметричен относительно этой линии, то его две части будут выглядеть идентично. Это как две близнеца, смотрят друг на друга и улыбаются.
Ну а как насчет зеркальной симметрии? Представь себе, что отрезок стоит перед зеркалом. Если он симметричен относительно плоскости зеркала, то его отражение будет выглядеть точно так же. Здорово, правда?
Ты понял, какие замечательные свойства есть у симметрии отрезка? Оно приводит к красоте и гармонии. Так давай вместе изучать и наслаждаться этим удивительным феноменом!
Примеры симметрии отрезка

Ниже приведены примеры, иллюстрирующие симметрию отрезка:
-
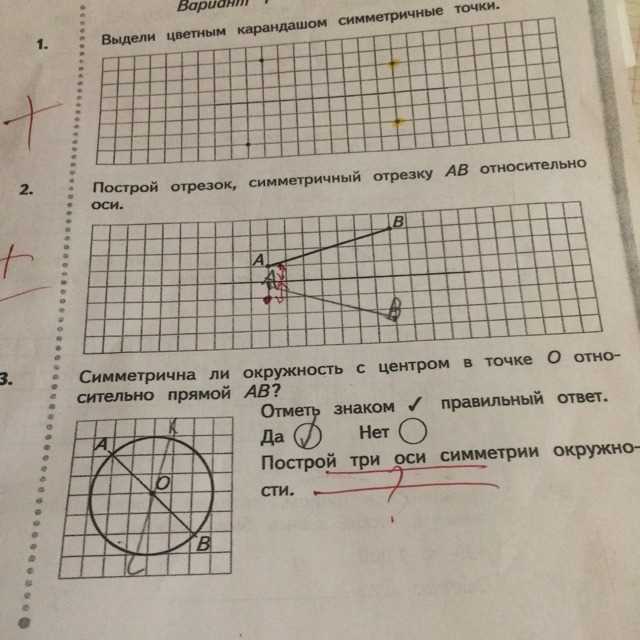
Пример 1: Отрезок AB, где A(-2, 0) и B(2, 0), является осью симметрии. Это означает, что точка, находящаяся на одинаковом расстоянии от точки A и B, будет находиться на этой оси симметрии.
-
Пример 2: Отрезок CD, где C(0, -3) и D(0, 3), является также осью симметрии. Все точки находятся на одинаковом расстоянии от точки C и D и симметричны относительно этой оси.
-
Пример 3: Отрезок EF, где E(-4, -4) и F(4, 4), также обладает симметрией. Отрезок EF является диагональю квадрата и является осью симметрии для квадрата, так как все точки находятся на одинаковом расстоянии от центра квадрата и от его диагонали.
Эти примеры демонстрируют, как в геометрии и математике используется понятие симметрии отрезка и как оно помогает в решении различных задач и построении геометрических фигур.






