Скаляры — это числовые значения, которые используются в математике для обозначения величин, не имеющих направления и ориентации. Они отличаются от векторов, которые представляют собой направленные величины.
Скалярные величины могут быть измерены и представлены с помощью чисел без дополнительной информации. Например, масса, время, длина и температура — все эти величины являются скалярами.
Скаляры также могут быть объединены с помощью различных математических операций, таких как сложение, вычитание, умножение и деление. Величины, которые имеют одинаковые единицы измерения и могут быть складываемыми или умножаемыми, являются скалярами.
Важно различать скаляры от векторов, так как векторы имеют направление и могут быть представлены с помощью координат. Скаляры, напротив, представляют собой только числа, представляющие значения величин без определенного направления.
Скаляр в математике
В математике есть такое понятие, как скаляр. Давай разберемся, что это такое и как оно связано с нашей повседневной жизнью.
Скаляр — это просто число. Ничего сложного. Но зачем оно нужно в математике? Дело в том, что скаляры позволяют нам описывать различные физические величины, такие как время, расстояние, масса и т.д.
Давай рассмотрим пример. Представь, ты едешь на велосипеде и за 2 часа проезжаешь 40 километров. Здесь время — это скаляр, потому что оно просто указывает, сколько времени ты потратил на поездку. Расстояние тоже является скаляром, потому что оно просто указывает, сколько километров ты проехал.
Скаляры очень полезны, потому что с их помощью можно проводить различные операции, такие как сложение и умножение. Например, ты едешь на велосипеде со скоростью 20 километров в час и проезжаешь 3 часа. Если умножить скорость на время, то получим расстояние: 20 км/ч * 3 часа = 60 километров. В этом примере скорость — это скаляр, потому что она просто указывает, как быстро ты двигаешься.
Так что скаляры — это просто числа, которые помогают нам описывать различные величины в математике и в нашей повседневной жизни. Не так сложно, верно? Вот и все, что нужно знать о скалярах! Если у тебя возникли вопросы или хочешь узнать больше, пиши в комментариях.
Определение скаляра
Теперь представь, что ты смотришь на звездное небо. Ты хочешь узнать, сколько звезд находится на небе. Но как ты можешь это сделать? Ты не можешь взять рулетку и измерить каждую звезду. Вместо этого, ты можешь использовать скалярные величины, такие как яркость, для определения количества звезд.
Так что же такое скаляр? Скаляр — это величина, которая имеет только значение (число) без определенной направленности. Он может представлять собой такие величины, как длина, масса, время, температура и т.д. Скалярный характер позволяет нам выполнять простые математические операции, такие как сложение и умножение, без необходимости учитывать направление или ориентацию.
Так что, при следующем путешествии по бескрайнему пространству или изучении звездного неба, помни, что скаляры помогут тебе измерить и понять окружающий мир без необходимости использовать сложные математические понятия.
Свойства скаляра
Вот несколько свойств скаляров:
- Аддитивность: Скаляры можно складывать и вычитать. Например, если у вас есть 5 яблок и 3 яблока, вы можете сложить их, чтобы получить общее количество яблок — 8 яблок.
- Умножение с числом: Скаляры можно умножать на числа. Например, если у вас есть 2 яблока, вы можете умножить его на 3, чтобы получить 6 яблок.
- Коммутативность: Порядок, в котором мы добавляем или умножаем скаляры, не имеет значения. Например, 2 + 3 = 3 + 2 и 2 * 3 = 3 * 2.
- Ассоциативность: Мы можем группировать скаляры в любом порядке. Например, (2 + 3) + 4 = 2 + (3 + 4) и (2 * 3) * 4 = 2 * (3 * 4).
- Инвариантность: Изменение единицы измерения не меняет значение скаляра. Например, если мы измеряем длину в футах или метрах, результат будет тот же — просто число без единицы измерения.
Скаляры широко используются в различных областях, от физики и экономики до информатики и биологии. Их свойства делают их удобными для работы с простыми величинами и выполнения различных вычислений.
Примеры применения скаляров
В физике:
- Векторная алгебра используется для описания движения тел и взаимодействия между ними. Например, скалярная величина, такая как масса, используется для измерения количества вещества в теле.
- Сила — еще один пример скалярной величины в физике. Она может быть представлена в виде числа без направления и используется для описания воздействия на объекты.
В экономике:
- В экономике используются скаляры для измерения различных величин, таких как цена, доход, объем продаж и потребление. Это позволяет анализировать экономическую ситуацию и принимать решения на основе числовых данных.
- Индексы потребительских цен — еще один пример использования скалярных величин в экономике. Они используются для измерения изменения цен на товары и услуги, что помогает анализировать уровень инфляции и его влияние на экономику.
В компьютерных науках:
- В компьютерных науках скаляры широко используются для представления числовых данных, таких как координаты пикселей на экране, числа для математических операций и другие параметры.
- Также скалярные величины используются в алгоритмах и программировании для выполнения различных операций и вычислений.
Вот лишь несколько примеров, как скаляры применяются в различных областях нашей жизни. Их использование помогает нам измерять, анализировать и понимать различные физические, экономические и компьютерные процессы. Без них наш мир был бы менее измеримым и понятным. Знание математики и понимание скаляров дает нам возможность улучшать, развивать и совершенствовать нашу жизнь и окружающий нас мир. Как вы применяете скаляры в своей жизни?
Отличие скаляра от вектора

Скаляр

Скаляр — это математический объект, который описывает величину без учета направления. Скаляром могут быть числа, как положительные, так и отрицательные. Они не имеют ориентации и не зависят от координатной системы. Примерами скаляров могут служить время, температура, масса и прочие физические величины.
Скаляры могут применяться в математических операциях, таких как сложение, вычитание, умножение и деление. Они могут быть складываны и умножаться на другие скаляры, а также на векторы. Но при этом скалярное умножение вектора на скаляр позволяет только изменять его величину, сохраняя при этом направление.
Вектор
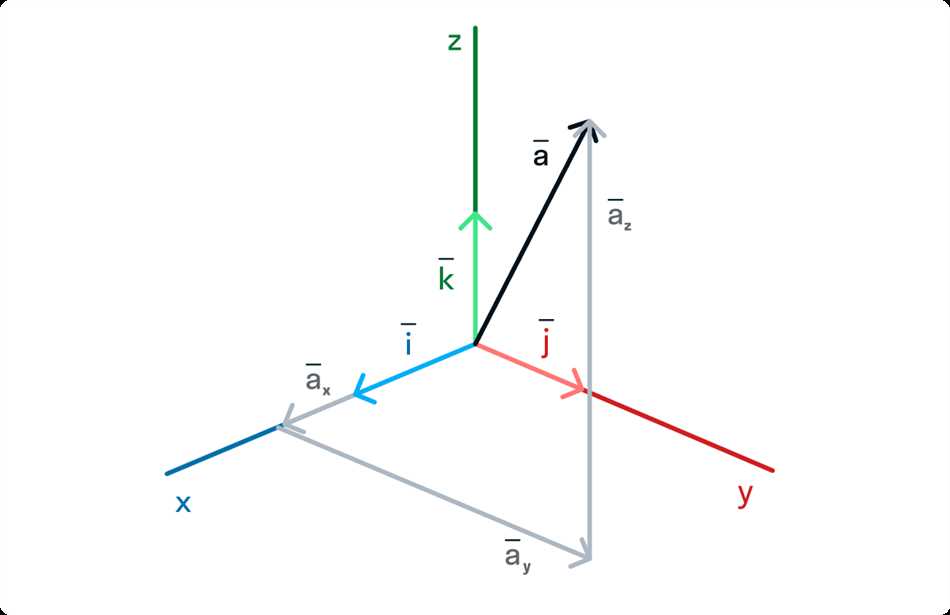
Вектор — это математический объект, который описывает величину и направление. Векторы могут быть изображены в виде стрелок, где длина стрелки представляет собой величину, а направление указывает на ориентацию. Примерами векторов могут служить силы, скорости, смещения и другие физические величины.
Векторы могут складываться и вычитаться друг из друга, а также умножаться на скаляры. Однако, у векторов также есть операция скалярного произведения, которая позволяет найти проекцию одного вектора на другой. Это позволяет определить угол между двумя векторами и выполнять сложные операции, такие как определение силы приложенной к объекту или решение задач динамики.
Заключение
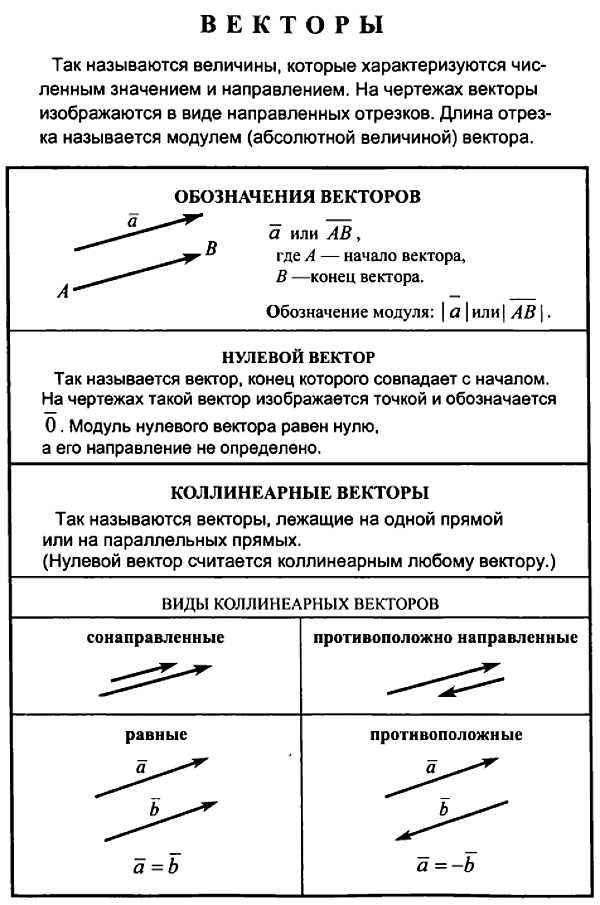
Таким образом, отличие между скаляром и вектором заключается в том, что скаляр представляет собой величину без учета направления, тогда как вектор описывает и величину и его направление. Использование скаляров или векторов зависит от конкретной математической операции или физической задачи, которую необходимо решить.