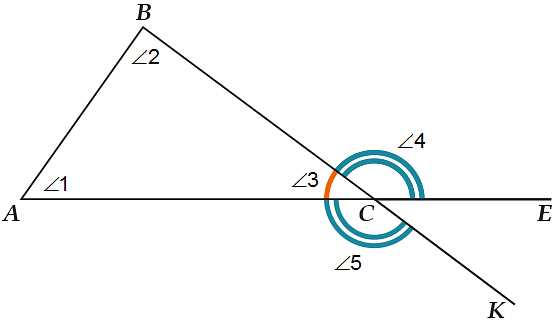
Треугольник — это геометрическая фигура, состоящая из трех прямых отрезков, образующих три вершины и три угла. Эта фигура широко применяется не только в математике, но и во многих других областях, включая физику. В физике треугольники часто используются для определения расстояний и измерения углов. Например, в геодезии треугольники используются для измерения расстояний между точками на земной поверхности. Треугольники также играют важную роль в тригонометрии, которая является важной математической основой для физики. Основные свойства треугольника включают сумму углов треугольника, которая равна 180 градусам, а также теорему Пифагора, которая гласит, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин двух острых углов. Таким образом, треугольник является важным элементом в физике и имеет множество применений в различных областях этой науки.
Определение треугольника
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Он является простейшей многоугольной фигурой и имеет огромное значение не только в математике, но и во многих других областях, включая физику.
Три стороны треугольника объединены в три вершины, а три угла образуются в этих вершинах. Каждая сторона треугольника соединяет две вершины, а угол образуется при пересечении двух сторон.
Треугольник можно классифицировать по различным характеристикам, таким как длины сторон и величины углов. Например, если все три стороны треугольника равны, то он называется равносторонним треугольником.
Также треугольник можно классифицировать по величине углов. Если все углы треугольника меньше 90 градусов, то он называется остроугольным треугольником. Если один из углов равен 90 градусов, то треугольник называется прямоугольным. А если хотя бы один угол больше 90 градусов, то его называют тупоугольным треугольником.
Важно отметить, что сумма углов треугольника всегда равна 180 градусов. Это свойство треугольника известно как теорема о сумме углов треугольника, которая была доказана великим греческим математиком Эвклидом.
Треугольники являются неотъемлемой частью многих областей науки и техники. Например, в физике треугольники используются для анализа сил и векторов, а также для построения моделей и диаграмм. Благодаря своей простоте и универсальности, треугольники являются одним из основных инструментов для понимания и изучения окружающего мира.
Так что следующий раз, когда увидишь треугольник, задумайся о его уникальных свойствах и важном значении в нашей жизни. Они повсюду вокруг нас, и понимание их структуры и свойств помогает нам развивать наши знания и навыки.
Геометрические свойства треугольника

Основные геометрические свойства треугольника включают:
- Углы треугольника: Треугольник состоит из трех углов, сумма которых всегда равна 180 градусам. Это называется свойством суммы углов треугольника.
- Стороны треугольника: Стороны треугольника могут быть разной длины, и каждая сторона может быть либо больше, либо меньше других сторон.
- Площадь треугольника: Площадь треугольника можно вычислить, зная длины его сторон или высоты и базы.
- Высоты треугольника: Треугольник имеет три высоты, которые являются перпендикулярными отрезками, опущенными из вершин к противоположным сторонам.
- Медианы треугольника: Треугольник имеет три медианы, которые являются отрезками, соединяющими вершины треугольника с серединами противоположных сторон.
- Радиусы вписанной и описанной окружностей: В треугольнике можно вписать окружность (окружность, которая касается всех трех сторон) и описать окружность (окружность, которая проходит через все три вершины).
Геометрические свойства треугольника имеют практическое применение во многих областях. Например, в физике, свойства треугольника могут использоваться для определения углов и расчета силы и направления векторов. В архитектуре и дизайне, знание геометрических свойств треугольника помогает создавать красивые и устойчивые конструкции.
Итак, геометрические свойства треугольника — это основные характеристики, которые определяют его форму и структуру. Понимание этих свойств позволяет нам анализировать и использовать треугольники в различных ситуациях и приложениях. Вы готовы к изучению геометрии треугольника и его свойств?
Треугольник и его геометрические формулы
Треугольник — это многоугольник с тремя сторонами и тремя углами. Его особенностью является то, что сумма всех его углов всегда равна 180 градусов. Это свойство треугольника известно как сумма углов треугольника и является одним из фундаментальных свойств геометрии.
Три главных типа треугольников, которые мы можем выделить, это прямоугольный, равнобедренный и равносторонний. Прямоугольный треугольник имеет один прямой угол, равнобедренный треугольник имеет две равные стороны и два равных угла, а равносторонний треугольник имеет все стороны одинаковой длины.
Формулы для вычисления площади, периметра и других параметров треугольника могут быть очень полезными. Например, формула для вычисления площади треугольника по его сторонам называется формулой Герона. Она имеет вид:
S = √(p × (p — a) × (p — b) × (p — c))
где S — площадь треугольника, p — полупериметр, a, b, c — стороны треугольника. Важно, чтобы треугольник был невырожденным, то есть стороны треугольника должны удовлетворять неравенству треугольника: сумма любых двух сторон должна быть больше третьей стороны.
Вот еще несколько полезных формул для треугольника:
- Периметр треугольника: P = a + b + c
- Высота треугольника: h = (2 × S) / a
- Медианы треугольника: медианы делят каждую сторону на две равные части, и их длины можно вычислить с использованием следующей формулы:
ma = 0.5 * √(2 * b2 + 2 * c2 — a2)
mb = 0.5 * √(2 * a2 + 2 * c2 — b2)
mc = 0.5 * √(2 * a2 + 2 * b2 — c2)
Формулы для треугольника могут иметь широкое применение в различных ситуациях. Например, в физике треугольники могут использоваться для вычисления силы трения, определения равнодействующей сил и других физических параметров. Имея точные математические формулы и умение правильно применять их, мы можем получать более достоверные и точные результаты в наших исследованиях и расчетах.
Так что не пренебрегай знанием формул для треугольника, дорогой читатель. Они могут пригодиться в самых неожиданных ситуациях, и ты сможешь проявить себя настоящим математическим гением! Погрузись в изучение треугольников и открой их удивительный и многогранный мир.
Треугольник в физике
Давайте поговорим о треугольнике в физике. И да, я знаю, что это может показаться необычной темой для обсуждения, но, поверьте мне, треугольники играют важную роль в мире физики.
Треугольник — это геометрическая фигура, состоящая из трех сторон и трех углов. Видимо, вы задаетесь вопросом: «Каким образом треугольник связан с физикой?» Отличное предположение, и я рад, что вы обратили внимание на это. Допустим, у нас есть треугольная плоская рамка, и мы оказываем на нее силы в разных направлениях. Интересно, как эти силы влияют на равновесие рамки?
Здесь на помощь приходит треугольник сил — концепция, которая помогает нам понять, как силы взаимодействуют друг с другом. Представьте себе, что каждая из сил представлена в виде вектора в плоскости рамки. Проведя линии от концов векторов, мы получим треугольник сил.
Теперь вопрос: что мы можем узнать из анализа треугольника сил? Во-первых, мы можем определить, является ли рамка в равновесии или нет. Если треугольник сил замкнут и образует сумму нулевой вектор, то рамка находится в равновесии. Давайте посмотрим на пример:
- Сила A направлена вверх с величиной 10 Н
- Сила B направлена вниз с величиной 5 Н
- Сила C направлена вправо с величиной 8 Н
Если мы нарисуем треугольник сил с этими значениями, мы увидим, что сумма векторов равна нулевому вектору. Это означает, что рамка находится в равновесии.
Вторым аспектом, о котором можно узнать из треугольника сил, является угол между силами. Угол определяет направление суммарной силы на рамку. Если угол равен 180 градусам, то суммарная сила направлена противоположно любой из векторных сил. Если угол между силами равен нулю градусам, тогда суммарная сила будет направлена вдоль одной из векторных сил.
Третьим аспектом является использование треугольника сил для нахождения суммарной силы и ее направления. Это особенно полезно, когда на рамку действуют несколько сил под углами друг к другу. Найдя сумму векторов, мы можем определить силу, с которой действуют на рамку.
Так что, как мы видим, треугольники играют важную роль в физике, помогая нам анализировать и понимать силы, взаимодействующие между объектами. Они позволяют нам определить равновесие и направление суммарной силы.
Теперь, когда вы разобрались с треугольником в физике, вы можете задавать себе вопросы о том, какие другие фигуры, применяемые в геометрии, могут быть полезными в физике. И кто знает, может быть, ваше любопытство и исследовательский дух приведут к новым открытиям и применениям в мире науки.
Треугольник в физике: определение, свойства и применение
Основные свойства треугольника в физике:
- Сумма углов треугольника: в треугольнике сумма всех углов всегда равна 180 градусам. Это свойство позволяет использовать треугольники для анализа угловых взаимодействий природных явлений.
- Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это свойство позволяет решать задачи о расстояниях и скоростях тел в двухмерном пространстве.
- Тригонометрические функции: с помощью треугольников можно определить значения тригонометрических функций (синус, косинус, тангенс). Это позволяет анализировать и описывать колебательные и периодические процессы в физике.
Применение треугольника в физике:
- Расчет геометрических параметров тел и конструкций.
- Определение расстояний и направлений в пространстве.
- Исследование и анализ движения тел.
- Анализ угловых взаимодействий и изменений направления.
- Определение соотношений между различными величинами и параметрами в физических явлениях.
Треугольник является одной из основных фигур в физике, которая позволяет упростить и облегчить анализ и решение различных задач. Умение работать с треугольниками и использовать их свойства является неотъемлемой частью физической подготовки и понимания принципов физических явлений.