Треугольный параллелепипед – это трехмерная геометрическая фигура, которая обладает особенной структурой. Он состоит из шести прямоугольных граней, из которых три являются прямоугольными треугольниками. Такой вид параллелепипеда отличается своей необычной формой, которая придает ему особый внешний вид и уникальные свойства.
Треугольный параллелепипед часто используется в конструкциях и архитектурных проектах, так как его форма обеспечивает прочность и стабильность. Кроме того, его особенности делают его непременным элементом при моделировании и визуализации объектов в трехмерной графике.
Определенное количество площади каждой грани и объем треугольного параллелепипеда позволяют использовать его для различных целей, включая строительство, дизайн и инженерные решения. Треугольный параллелепипед – это одна из многих уникальных фигур, которая имеет свои особенности в геометрической форме и широкое применение в различных областях.
Описание треугольного параллелепипеда
Треугольный параллелепипед – это трехмерная фигура, имеющая шесть граней, у которой три из них являются треугольниками, а остальные три – прямоугольниками. Уникальность этой фигуры заключается в том, что основной прямоугольник делится на два треугольника общим ребром, которые являются соседними к граням параллелепипеда.
Часто встречается мнение, что треугольные параллелепипеды не существуют, так как невозможно найти реальный предмет с такой формой. Но мы не соглашаемся с такими утверждениями! Ведь геометрия это наука о формах и фигурах, которые существуют в нашем воображении, и они могут быть очень полезными в реальной жизни!
Треугольные параллелепипеды могут быть разных размеров и пропорций, как и обычные параллелепипеды. Например, мы можем представить себе маленький треугольный параллелепипед, который стоит на столе в вашей комнате или огромный треугольный параллелепипед, который служит основой для строительства моста.
Если задуматься о применении треугольных параллелепипедов, то станет понятно, что их форма может быть полезна для создания устойчивых и прочных конструкций. Треугольники известны своей жесткостью и стабильностью, поэтому параллелепипеды с треугольными гранями также наследуют эти качества. Для этой особенности треугольных параллелепипедов можно найти множество применений в различных областях, начиная от строительства и заканчивая инженерией.
Итак, друзья, треугольные параллелепипеды — это уникальные геометрические фигуры, которые могут быть как маленькими игрушками, так и поистине грандиозными конструкциями. Помните, что даже несуществующие в реальности объекты могут прекрасно служить нам в нашей воображаемой вселенной и приносить нам не только радость от изучения, но и полезность в нашей повседневной жизни. Вдохновляйтесь геометрией и исследуйте мир треугольных параллелепипедов!
Основные характеристики треугольного параллелепипеда
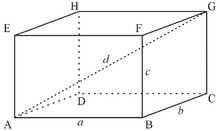
Что такое треугольный параллелепипед? Какие особенности и характеристики у него есть? Если вы интересуетесь геометрией и знакомством с различными геометрическими фигурами, то вам обязательно будет интересно узнать о треугольных параллелепипедах.
Треугольный параллелепипед представляет собой геометрическую фигуру, имеющую три треугольные грани и шесть кромок. Данная фигура отличается от обычного параллелепипеда, у которого все грани являются прямоугольными. Одна из основных особенностей треугольного параллелепипеда – наличие треугольных граней, которые могут быть равнобедренными или разносторонними.
Как же определяются основные характеристики такой геометрической фигуры? В первую очередь, стоит обратить внимание на площадь его граней. Сумма площадей трех треугольных граней даст нам площадь поверхности треугольного параллелепипеда. Размер сторон и углы этих треугольных граней могут быть различными, что позволяет создавать треугольные параллелепипеды разной формы и размеров.
Треугольный параллелепипед имеет также объем, который определяется умножением площади одной из оснований на высоту фигуры. Высота треугольного параллелепипеда – это расстояние между его основаниями, она может быть произвольной и зависит от размеров и конструкции данной фигуры.
Как высчитать объем треугольного параллелепипеда? Возьмите площадь основания (предположим, это треугольник), которая равна, например, 25 см². Перемножьте ее на высоту треугольного параллелепипеда (допустим, равна 10 см). Получим следующий результат: 25 см² * 10 см = 250 см³. Таким образом, объем параллелепипеда составляет 250 кубических сантиметров.
Основные характеристики треугольного параллелепипеда:
- Три треугольные грани;
- Шесть кромок;
- Различные размеры и углы треугольных граней;
- Площадь поверхности, определяемая суммой площадей граней;
- Объем, рассчитываемый как произведение площади основания на высоту;
- Разнообразие форм и размеров.
В итоге, хотя треугольный параллелепипед не является типичной геометрической фигурой, он всегда будет привлекать к себе внимание своими интересными характеристиками. Почему бы не попробовать нарисовать его с помощью линейки и карандаша? Маленький эксперимент поможет вам лучше представить эту фигуру в пространстве и лучше понять ее основные характеристики.
Свойства треугольного параллелепипеда
1. Уникальная форма
Особенностью треугольного параллелепипеда является его форма. В отличие от обычного параллелепипеда с прямоугольными гранями, у треугольного параллелепипеда грани образуют треугольники. Эта форма делает его особенно уникальным и привлекательным.
2. Три равные пары граней

Всякое параллелепипед имеет три пары противолежащих граней, которые параллельны друг другу. У треугольного параллелепипеда при этом есть еще одна особенность — каждая пара граней, образующих основания, является треугольной. Таким образом, у треугольного параллелепипеда три равные пары граней, что придает ему устойчивость и привлекательность.
3. Шесть граней
Треугольный параллелепипед имеет шесть граней, по одной на каждую сторону. Каждая грань представляет собой треугольник, что делает его структуру простой и понятной.
4. Устойчивость
Благодаря своей уникальной форме и параллельным граням треугольного параллелепипеда, он обладает высокой степенью устойчивости. Это позволяет ему противостоять внешним силам и сохранять свою форму.
5. Удобство конструкции

Благодаря своим свойствам треугольного параллелепипеда может быть удобен для конструирования различных предметов и сооружений. Его устойчивость и привлекательная форма делают его отличным выбором для создания столов, полок, стеллажей и многого другого.
6. Разнообразие размеров
Треугольные параллелепипеды могут быть различных размеров, от маленьких и компактных до больших и объемных. Это позволяет использовать их в различных ситуациях и вариантах, подходящих для каждой конкретной задачи.
Такие свойства треугольного параллелепипеда делают его уникальным и интересным объектом. Он обладает не только эстетической привлекательностью, но и функциональностью, что делает его полезным во многих сферах жизни.
Что такое треугольный параллелепипед
Другими словами, треугольный параллелепипед образуется, когда треугольные грани складываются вдоль их боковых ребер.
Основные характеристики треугольного параллелепипеда:
- Боковые грани: Треугольные грани, которые соединяют основания параллелепипеда.
- Боковые ребра: Ребра, на которых расположены боковые грани.
- Основания: Две параллельные треугольные грани, расположенные на противоположных концах параллелепипеда.
- Высота: Расстояние между основаниями параллелепипеда. В случае треугольного параллелепипеда, высота проходит по боковому ребру.
- Объем: Объем треугольного параллелепипеда можно вычислить по формуле: V = (основание * высота) / 2, где основание — площадь одного из треугольников-оснований, а высота — высота параллелепипеда.
Треугольные параллелепипеды могут быть использованы в различных сферах, например, в архитектуре и строительстве для создания устойчивых и прочных конструкций.