Запятая в математике: роль и особенности использования

Запятая — это пунктуационный знак, который не только широко используется в языке, но также имеет свое применение в математике. Помимо разделения чисел на тысячи, запятая может быть использована в математических выражениях для разделения целой и десятичной части числа. Она играет важную роль в создании числовой системы и облегчает понимание и запись чисел. Запятая также используется в математических формулах для разделения переменных и участков выражений. В этой статье мы рассмотрим определение запятой в математике и ее основное применение.

Определение и свойства запятой

Запятая, возможно, кажется небольшой и незаметной, но она играет громадную роль в математике. Она помогает нам разделять целую и десятичную части числа, а также вносит ясность в запись больших чисел. Запятая отделяет разряды чисел на сегменты и делает их более читабельными.

Одно из свойств запятой – ее позиция в числе. В математике мы договорились, что запятая ставится после каждых трех разрядов (тысячных). Например, число 2000 записывается с использованием запятой как 2,000. Затем, если число становится очень большим, запятая будет повторяться через каждые три разряда, чтобы облегчить чтение и понимание числа. Например, цена бриллианта может быть $1,245,678.23, где каждая запятая показывает разделение разрядов.

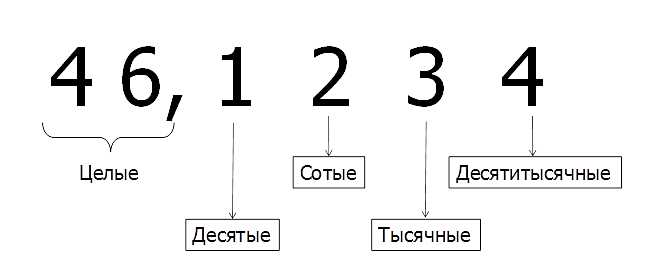
Запятая также играет важную роль при записи десятичных дробей. Десятичная запятая разделяет целую и десятичную части числа. Например, число 3.14159 означает, что у нас есть 3 целые единицы и 14159 частей одной единицы.

Итак, дорогой читатель, запятая в математике – это маленький символ, имеющий огромное значение. Он помогает разделять разряды и сделать запись чисел более понятной и удобной для чтения. Без запятой мы были бы потеряны при попытке разобраться с большими числами и десятичными дробями. Так что давайте будем благодарны запятой за ее незаменимую роль в мире математики!

Понятие запятой в математике

Давайте поговорим о запятой в математике. Когда мы слышим это слово, мы обычно ассоциируем его с пунктуацией или разделительным знаком в письменном тексте. Но в математике запятая имеет свое собственное значение и применение.

В математике запятая обычно используется как десятичный разделитель. Он отделяет целую часть числа от десятичной. Например, если у нас есть число 3,14159, запятая отделяет целую часть 3 от десятичной части 14159. Запятая помогает нам ориентироваться в числах и понять их значение более точно.

Но роль запятой в математике не ограничивается только десятичными разделителями. Он также используется для разделения элементов в множествах или последовательностях. Например, если у нас есть множество {1, 2, 3, 4}, запятая разделяет каждый элемент, чтобы показать, что они являются отдельными числами.

Запятая также играет важную роль в записи больших чисел. Он помогает нам разделять разряды числа для более удобного чтения и понимания. Например, число 1 000 000 записывается с помощью запятой между каждым разрядом, чтобы показать, что его значение равно одному миллиону.

Итак, может показаться, что запятая — это просто маленький знак препинания, но в математике она имеет глубокое значение и широкий спектр применений. Он помогает нам понять числа, записывать их правильно и ориентироваться в сложных математических концепциях. Без запятой математика была бы гораздо менее точной и понятной.

Так что давайте продолжим использовать запятую в наших математических вычислениях и будем благодарны за ее существование. Убедитесь, что вы правильно используете запятую в своих расчетах и не забывайте о ее важности. Запятая — это небольшой символ, который делает большую разницу в нашем понимании математики.

Основные свойства запятой

Первое, что нужно знать о запятой, — это то, что она используется для разделения элементов в предложении. Она помогает нам структурировать наши мысли и делает текст более читабельным. Когда мы говорим вслух, мы используем паузу, чтобы разделить различные части предложения, и запятая выполняет ту же функцию в письменной форме.

Однако запятая также может быть использована для создания эффекта неожиданности или усиления в предложении. Запятая может быть поставлена после слова или фразы, чтобы добавить дополнительную информацию или выделить важные детали. Она играет роль акцента, который привлекает внимание читателя и делает текст более интересным.

Например: «Я встретил моего друзяшку, который уехал в другую страну, чтобы учиться.» Здесь запятая после «друзяшку» добавляет информацию о том, что он уехал в другую страну. Она делает предложение более полным и позволяет нам лучше понять контекст.

Кроме того, запятая используется для разделения элементов в списках. Она помогает нам ясно указать каждый отдельный элемент, делая текст более структурированным и понятным.

Например: «На моем столе лежат книги, ручки, блокнот и компьютер.» Здесь запятые указывают на отдельные элементы в списке и позволяют нам легко их различить.

Теперь, когда вы знаете основные свойства запятой, вы можете использовать ее правильно в своих написанных текстах. Это поможет сделать ваш текст более понятным и интересным. Продолжайте практиковаться и замечайте, как запятая может изменить смысл предложения. Когда вы ее правильно используете, ваш текст станет еще лучше!

Интерпретация запятой в различных областях математики

1. Арифметика

В арифметике запятая часто используется для разделения десятичных дробей. Например, число 3,14 представляет собой приближенное значение числа Пи. Запятая также может использоваться для разделения разрядов числа при их записи, что позволяет легче читать и интерпретировать большие числа. Например, число 1,000,000 — это один миллион.

2. Геометрия

В геометрии запятая может использоваться для обозначения координат точек на плоскости или в пространстве. Например, точка A с координатами (2, 3) находится на двух единицах вправо и трех вверх от начала координат. Запятая также может использоваться для обозначения отрезка или интервала на числовой оси. Например, отрезок [1, 5] включает числа от 1 до 5 включительно.

3. Алгебра

В алгебре запятая может использоваться для обозначения промежуточных шагов при решении уравнений или выражений. Например, при решении уравнения 2x + 3 = 7, мы можем написать 2x = 7 — 3, чтобы выразить x в одном шаге. Запятая также может использоваться для обозначения коэффициентов в многочлене или матрице.

4. Теория вероятности

В теории вероятности запятая используется для обозначения десятичной разделительной запятой в вероятностях. Например, вероятность выпадения головы при подбрасывании монеты обычно обозначается как 0,5 — это означает, что вероятность головы составляет половину или 50%.

5. Статистика

В статистике запятая может использоваться для разделения значений в выборке или для указания разделителя между двумя различными переменными. Например, в выборке [1, 2, 2, 3, 4, 5] каждое значение разделено запятой. Запятая также может использоваться для обозначения десятичной точности в статистических показателях, таких как среднее значение или стандартное отклонение.

6. Комбинаторика

В комбинаторике запятая может использоваться для обозначения различных комбинаций или перестановок. Например, комбинаторное число «5 по 2» записывается как C(5, 2) или 5C2 — это означает, что мы выбираем 2 элемента из 5 возможных.

7. Математическая логика

В математической логике запятая может использоваться для обозначения логического «и». Например, выражение «A и B» обычно записывается как A, B. Запятая также может использоваться для разделения предпосылок в математических доказательствах или логических выражениях.

8. Дифференциальное исчисление

В дифференциальном исчислении запятая может использоваться для обозначения производной. Например, производная функции y = f(x) по переменной x обозначается f'(x) или dy/dx, где запятая показывает, что мы производим функцию по переменной x.

9. Интегралы

В интегралах запятая используется для обозначения границ интегрирования. Например, определенный интеграл функции f(x) от a до b обозначается как ∫[a,b] f(x) dx, где запятая разделяет нижнюю и верхнюю границы интегрирования.

10. Анализ функций

В анализе функций запятая может использоваться для разделения аргументов функции или для обозначения множества значений функции. Например, функция f(x, y) принимает два аргумента x и y. Запятая также может использоваться для обозначения принадлежности значения функции определенному множеству. Например, значение функции f(x) принадлежит множеству целых чисел, если мы пишем f(x) ∈ Z.

Заключение

Как видим, запятая играет важную роль в различных областях математики, от арифметики и геометрии до дифференциальных уравнений и математической логики. Инициатива использования запятой и ее интерпретация зависят от контекста задачи и области математики, в которой она применяется. Разностороннее использование запятой позволяет нам более точно и ясно формулировать математические понятия и решать сложные задачи. Так что следующий раз, когда вы увидите запятую в математической формуле, помните о ее важной роли в понимании и применении математики!

Применение запятой в математике

Удивительно, правда? Оказывается, когда мы говорим о больших числах, запятая помогает нам наглядно представить разряды и упростить чтение и запись чисел.

Итак, как же работает запятая в числах? Распрощаемся с простыми знаками пунктуации и рассмотрим упрощенный пример: 1234567. В одну мгновение этот набор цифр может выглядеть непонятно и запутанно. Однако, если добавить запятые между разрядами, мы получим 1,234,567. Теперь намного проще разобраться, правда? Каждая запятая позволяет нам видеть, что число состоит из тысяч, миллионов, миллиардов и так далее.

Теперь давайте посмотрим на более сложный пример. Представьте, что у вас есть число 876543210. Без запятых это число может вызвать головную боль, не так ли? Но если мы добавим запятые, то получим 876,543,210. Теперь очевидно, что это число состоит из сотен миллионов, десятков тысяч и единиц.

Итак, для чего нам нужны эти разделители? Они помогают нам легче читать, понимать и записывать числа, особенно когда они имеют много разрядов. Обратите внимание, что количество запятых определяется местными правилами, и каждая страна может иметь свои специфические требования.

Но применение запятой в математике не ограничивается только разделением разрядов чисел. Она также используется в десятичных числах, чтобы разделить целую часть от дробной. Например, в числе 3,14159 запятая отделяет целую часть (3) от дробной (0,14159). Или в числе 0,5 запятая отделяет целую часть от десятичной.

Таким образом, применение запятой в математике является неотъемлемой частью записи и понимания чисел. Она делает числа более читабельными и помогает нам работать с ними более эффективно. Так что следующий раз, когда вы увидите запятую в числе, не забудьте о ее важной роли и благодарите ее за помощь в понимании и упрощении математического мира!

Использование запятой в десятичных дробях

Использование запятой в десятичных дробях имеет важное значение, поскольку она помогает нам задать точность числа. Например, если у нас есть число 3,1415926535, но мы хотим представить его с округлением до двух знаков после запятой, мы можем записать его как 3,14. Такое использование запятой позволяет нам сократить количество знаков после запятой и упростить представление числа без потери его основного значения.

Запятая также используется для разделения разрядов в больших числах. Например, число 1 000 000 записывается как 1,000,000. Это помогает нам легче читать и понимать большие числа и их структуру.

Запятая в десятичных дробях также играет важную роль при выполнении математических операций. Она помогает нам разделить целую и дробную части числа, что позволяет нам выполнять сложение, вычитание, умножение и деление с десятичными дробями без потери точности.

Таким образом, использование запятой в десятичных дробях необходимо для точного представления чисел и выполнения математических операций. Она позволяет нам задавать точность числа и упрощать его представление, а также понимать структуру больших чисел. Без использования запятой мы бы не смогли работать с десятичными дробями так эффективно и точно.

Применение запятой при задании координат

Для наглядности применения запятой при задании координат, представим себе плоскость с осями X и Y. Координаты точки на плоскости обозначаются парой чисел, разделенных запятой. Первое число в паре — это значение по оси X, а второе число — это значение по оси Y. Например, точка (3, 5) означает, что она находится на расстоянии 3 единиц от начала оси X и 5 единиц от начала оси Y.

Использование запятой при задании координат позволяет однозначно определить положение точки на плоскости. Она является разделителем значений по осям и помогает устранить двусмысленность. Например, если бы не было запятой, то пара чисел (35) могла бы интерпретироваться как точка на оси X или на оси Y. Запятая же позволяет нам эксплицитно указывать, какое число соответствует какой оси.

Кроме того, запятая может использоваться для задания точек в трехмерном пространстве. В этом случае координаты точки указываются тройкой чисел, разделенных запятой. Например, точка (2, 4, 6) находится на расстоянии 2 единиц от начала оси X, 4 единиц от начала оси Y и 6 единиц от начала оси Z.

Таким образом, использование запятой при задании координат — это важный элемент математического языка, позволяющий точно определить положение объектов на плоскости или в пространстве.

Запятая в математике: определение и применение

Применение запятой в математике может быть различным, в зависимости от контекста и специфики задачи. Основные области, где запятая используется, включают:

1. Перечисление элементов в списке: запятая используется для разделения элементов в списке чисел, переменных или выражений. Например: a, b, c.
2. Десятичная запятая: в некоторых странах, включая Россию, запятая используется как разделитель тысячных и десятичных разрядов в записи десятичных чисел. Например: 3,14.
3. Разделение целой и десятичной части: в некоторых системах записи десятичных чисел используется запятая для разделения целой и десятичной части. Например: 3,14.
4. Индекс запятой: в математической нотации запятую также можно использовать в качестве индекса или принадлежности к множеству. Например: x ∈ (0, 1).
5. Другие специфические случаи: в некоторых математических областях, таких как комбинаторика или теория графов, запятая может использоваться для обозначения особых взаимосвязей или операций.