Когда мы изучаем алгебру в восьмом классе, одним из основных понятий, с которым мы сталкиваемся, является аргумент. Аргумент — это числовое выражение или переменная, которая подставляется вместо параметра функции или в уравнение. Он может быть представлен в виде буквы, например «х», или как выражение, использование которого помогает решить задачу.
Понимание значения аргумента в алгебре важно, так как оно позволяет нам анализировать и решать различные уравнения и задачи. Знание, как выбирать и использовать аргументы, поможет нам в поиске решений и понимании, какие значения можно подставить, чтобы получить нужные результаты.
- Аргумент в алгебре 8 класс
- Понятие аргумента
- Геометрическая интерпретация аргумента
- Полярные координаты
- Операции с аргументами
- Примеры использования аргумента
- 1. Навигация и география
- 2. Векторная графика
- 3. Физика и инженерия
- 4. Компьютерные программы и робототехника
- Значение аргумента в алгебре 8 класс
- Примеры:
Аргумент в алгебре 8 класс
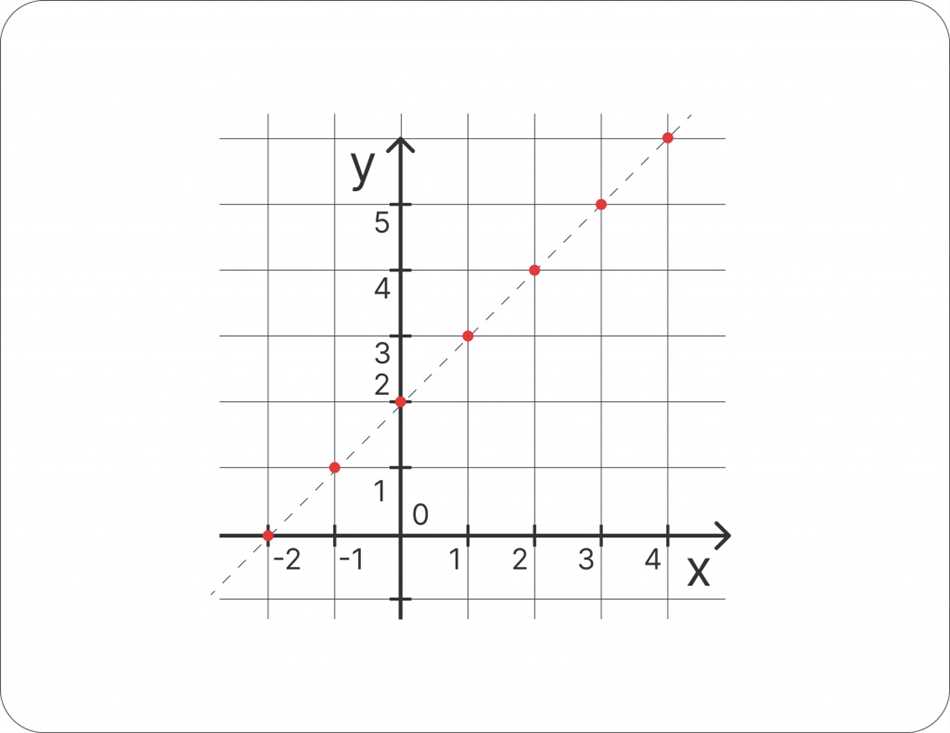
Представь себе, что на плоскости есть точка, которая является концом вектора. Если провести луч из начала координат до этой точки, то его угол с осью Ox будет являться аргументом вектора.
Аргумент задается в радианах и может быть положительным или отрицательным, в зависимости от направления поворота вектора. Если вектор поворачивается против часовой стрелки, то аргумент положительный. Если же вектор поворачивается по часовой стрелке, то аргумент будет отрицательным.
Зачем нам нужно знать аргумент в алгебре? Затем, что аргумент позволяет нам определить положение вектора на плоскости и решать различные алгебраические задачи. Например, зная аргументы двух векторов, мы можем определить их сумму или разность. Также, аргументы полезны при умножении комплексных чисел, где аргументы складываются.
Надеюсь, этот небольшой обзор помог тебе понять, что такое аргумент в алгебре. Разве не интересно, как одно понятие может так многое значить и помогать в решении задач? Всегда будь внимателен к деталям и находи применение для всего, что учишься!
Понятие аргумента
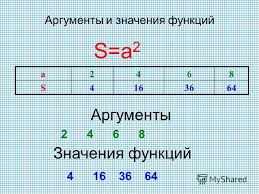
Аргумент может быть представлен в различных форматах, в зависимости от контекста задачи. Например, в математике аргумент может быть числом, переменной или выражением. В физике, биологии и других науках аргументом могут быть физические величины, временные интервалы или другие параметры.
Важно понимать, что значение аргумента может влиять на результат функции. Например, если у нас есть функция, описывающая расход топлива автомобиля в зависимости от скорости, то аргументом этой функции будет скорость автомобиля. Изменение скорости будет влиять на результат — расход топлива.
Таким образом, понимание понятия аргумента является важным для решения различных задач и проблем. Оно позволяет нам анализировать и понимать зависимости, прогнозировать результаты и принимать обоснованные решения.
Геометрическая интерпретация аргумента
Давайте представим, что мы находимся в математическом мире и перед нами находится плоская система координат, где ось X — это вещественная ось, а ось Y — это мнимая ось. Ось X ориентирована вправо, а ось Y — вверх.
Представьте, что у нас есть комплексное число z = a + bi, где a и b — это вещественные числа. При такой интерпретации, а — это координата числа z по оси X, а b — по оси Y. То есть, горизонтальное перемещение от начала координат до точки z составляет a, а вертикальное перемещение — b.
Сейчас давайте посмотрим нашу плоскость и весьма интересный комплекс z. Смотрите, он находится под углом с осью X. Этот угол, который образуется между осью X и линией, соединяющей начало координат и точку z, называется аргументом числа z.
А что будет, если число z находится выше оси X? А если ниже? Или на самой оси X? Или между осью X и осью Y? Каждая из этих позиций соответствуют определенному значению аргумента. Все эти значения можно измерить в градусах или радианах.
Геометрическая интерпретация аргумента позволяет нам понять, какие числа находятся на одной лучистой линии, отстоящей от начала координат на определенное расстояние. Она также помогает визуализировать операции со сложением и умножением комплексных чисел, что позволяет нам лучше понять их свойства.
Полярные координаты
Каждая точка в полярных координатах задается двумя значениями: радиусом (r) и аргументом (θ). Радиус (r) определяет расстояние от начала системы координат до точки, аргумент (θ) указывает угол от оси OX до радиус-вектора точки. Аргумент (θ) измеряется в градусах или радианах, в зависимости от системы измерения, используемой в задаче.
Главная особенность полярных координат заключается в том, что они позволяют легко представить круговое движение и повороты. Например, если мы хотим описать точку, движущуюся по окружности с радиусом 5 и центром в начале координат, мы можем использовать полярные координаты (r=5, θ). Начальное значение аргумента (θ) будет задавать начальное положение точки, а приращение значения аргумента будет определять каждый следующий момент времени и положение точки на окружности.
Полярные координаты также позволяют удобно описывать сложные формы, такие как эллипсы или спирали. Используя различные значения радиуса и аргумента, можно задать форму и размеры этих фигур.
Важно помнить, что полярные координаты и прямоугольные координаты (x, y) связаны между собой следующими формулами:
- x = r * cos(θ)
- y = r * sin(θ)
Главное преимущество использования полярных координат заключается в их простоте и наглядности для определенных задач. Они позволяют более интуитивно понять и описать положение и движение точек на плоскости и широко применяются в математике, физике, инженерии и других науках.
Операции с аргументами
Одной из основных операций с аргументами является сложение. При сложении аргументов мы складываем их значения и получаем новое число. Например, если мы имеем аргументы a=3 и b=4, то их сумма будет равна a + b = 3 + 4 = 7.
В алгебре также используется вычитание. Вычитание аргументов происходит путем вычитания значения одного аргумента из значения другого аргумента. Например, если a=5 и b=2, то a — b = 5 — 2 = 3.
Умножение – еще одна операция с аргументами. При умножении аргументов мы перемножаем их значения и получаем новое значение. Например, если a=2 и b=3, то a * b = 2 * 3 = 6.
Еще одна операция, которую мы можем выполнять с аргументами, – деление. При делении аргумента на другой аргумент мы получаем результат, который является частным этих аргументов. Например, если a=10 и b=2, то a / b = 10 / 2 = 5.
Также мы можем проводить операцию возведения в степень. Возведение аргумента в степень означает умножение аргумента самого на себя определенное количество раз. Например, если a=4, и мы хотим возвести его в квадрат, то a^2 = 4 * 4 = 16.
Кроме того, мы можем применять и другие операции с аргументами, такие как извлечение квадратного корня, извлечение кубического корня, нахождение остатка от деления и др. Все эти операции позволяют нам работать с аргументами и получать новые значения.
Таким образом, операции с аргументами позволяют нам выполнять различные действия с числами и выражениями в алгебре. Они помогают нам решать задачи и находить ответы на интересующие вопросы. При изучении алгебры важно освоить все эти операции и научиться применять их в разных ситуациях. А теперь давайте попробуем решить несколько задачек, чтобы закрепить полученные знания!
Примеры использования аргумента
Оказывается, аргумент имеет не только математическое значение, но и находит свое применение в различных областях.
1. Навигация и география
Давайте представим ситуацию, когда вы собираетесь путешествовать на машине в другой город. Вы можете использовать аргумент, чтобы определить направление вашего движения. Например, если вам необходимо ехать на юг, то у вас будет отрицательный аргумент, а если на север – положительный. Таким образом, аргумент поможет вам ориентироваться на дороге и выбрать правильное направление.
Также аргумент можно использовать для определения местоположения объектов на глобусе. Например, географы используют аргумент при указании координат точек на картах и навигационных системах.
2. Векторная графика
Еще одна область, где аргумент находит свое применение, это векторная графика. Векторный графический редактор позволяет задавать координаты точек на плоскости с помощью аргумента. Например, чтобы нарисовать отрезок между двумя точками, можно указать их координаты и аргументы, чтобы определить угол наклона отрезка.
Также аргумент используется в vj-программах для задания угла поворота и масштабирования объектов.
3. Физика и инженерия
Аргумент применяется и в физике. Например, при решении задач на механику или электромагнетизм, аргумент используется для определения направления движения или силы.
В инженерии аргумент также находит свое применение. Например, при проектировании мостов или зданий, аргумент используется для определения угла наклона конструкции.
4. Компьютерные программы и робототехника
В сфере информационных технологий аргумент широко применяется при разработке компьютерных программ и робототехники. Например, аргумент используется для задания угла поворота графических объектов на экране или для программирования движений робота.
Как видим, примеров использования аргумента в повседневной жизни и различных областях деятельности очень много. Он помогает нам ориентироваться, решать задачи и задавать координаты точек на плоскости. Изучение аргумента может быть полезным не только для понимания математических концепций, но и для повседневной практической жизни.
Значение аргумента в алгебре 8 класс
Аргументом числа называется угол, который это число образует с положительным направлением оси абсцисс.
Значение аргумента определяется в градусах или радианах и имеет следующие особенности:
- Аргумент числа может быть положительным, отрицательным или равным нулю.
- Если аргумент числа равен нулю, то это число находится на положительном направлении оси абсцисс (действительная положительная ось).
- Если аргумент числа положителен, то это число находится в I или II координатной четверти.
- Если аргумент числа отрицателен, то это число находится в III или IV координатной четверти.
Определения:
- Если точка M(x, y) лежит на положительном направлении оси абсцисс, то ее аргумент равен 0.
- Если точка M(x, y) лежит на положительном направлении оси ординат, а x ≠ 0, то ее аргумент равен 90° (π/2 радиан).
- Если точка M(x, y) лежит на отрицательном направлении оси абсцисс, то ее аргумент равен ±180° (π радиан).
- Если точка M(x, y) лежит на отрицательном направлении оси ординат, а x ≠ 0, то ее аргумент равен -90° (-π/2 радиан).
- Θ — обозначение аргумента числа.
Примеры:
| Точка | Аргумент |
|---|---|
| (4, 0) | 0 |
| (0, 5) | 90° (π/2 радиан) |
| (-3, 0) | 180° (π радиан) |
| (0, -2) | -90° (-π/2 радиан) |