Математика — это одна из самых важных наук, которая изучает структуры, фигуры, пространство и числа. Она играет огромную роль в нашей повседневной жизни и имеет огромное значение в различных областях, начиная от финансов и экономики, и заканчивая физикой и компьютерными науками.
Одно из основных понятий в математике — это понятие значения. Значение может относиться как к числам, так и к переменным, функциям и другим математическим объектам. Оно позволяет нам определить, чему равен или может быть равен данный объект или выражение. Например, если у нас есть выражение «2 + 3», то значение этого выражения равно 5.
В данной статье мы рассмотрим различные примеры значений в математике и их применение в решении задач и теоретических заданий.
Определение значения в математике
С помощью значения мы можем понять, что означает каждое число, переменная или выражение в задаче или уравнении. Например, если у нас есть уравнение 2x + 3 = 7, значение x будет 2, потому что 2 умноженное на 2 плюс 3 равно 7. Значение x — это то, что делает это уравнение истинным.
Значение также может быть использовано для определения результатов вычислений. Представьте себе, что вы решаете сложную математическую задачу, и вы видите, что некоторые числа и выражения вам уже знакомы. Это может быть потому, что вы уже знаете их значение и можете использовать это знание, чтобы решить задачу быстрее и более точно.
Важно отметить, что значение в математике является абсолютным и неизменным. Оно не зависит от нашего мнения или интерпретации. Например, 2 всегда будет равно 2, независимо от того, как мы это понимаем или представляем. Это делает математику объективной и надежной для научных исследований и применений.
Значение в математике имеет большое значение для понимания и применения различных математических концепций. Оно помогает нам не только решать задачи и уравнения, но и анализировать и обобщать различные математические закономерности и связи. Использование значения позволяет нам более глубоко и точно изучать мир чисел и вычислений, и открывает перед нами множество возможностей для применения математики в реальной жизни.
Примеры значения в математике

1. Значение переменной
Одним из примеров значения в математике является значение переменной. Переменная — это символ, который представляет неизвестное или изменяющееся значение. Когда мы придаем переменной определенное значение, мы можем вычислить и получить значение выражения или функции, содержащей эту переменную.
Например, рассмотрим простое выражение 2x + 3, где x — переменная. Если мы придадим переменной x значение 5, то мы можем вычислить выражение следующим образом: 2 * 5 + 3 = 13. Таким образом, значение переменной x равно 5, а значение выражения 2x + 3 равно 13.
2. Значение выражения
Значение выражения — это результат вычисления математического выражения. Выражение может содержать числа, переменные и операторы, которые определяют математические операции, которые необходимо выполнить.
Например, рассмотрим выражение 3 + 4 * 2. Чтобы вычислить это выражение, мы следуем правилам приоритета операций и выполняем умножение перед сложением. Таким образом, мы получаем следующий результат: 3 + 4 * 2 = 3 + 8 = 11. Значение выражения 3 + 4 * 2 равно 11.
3. Значение функции
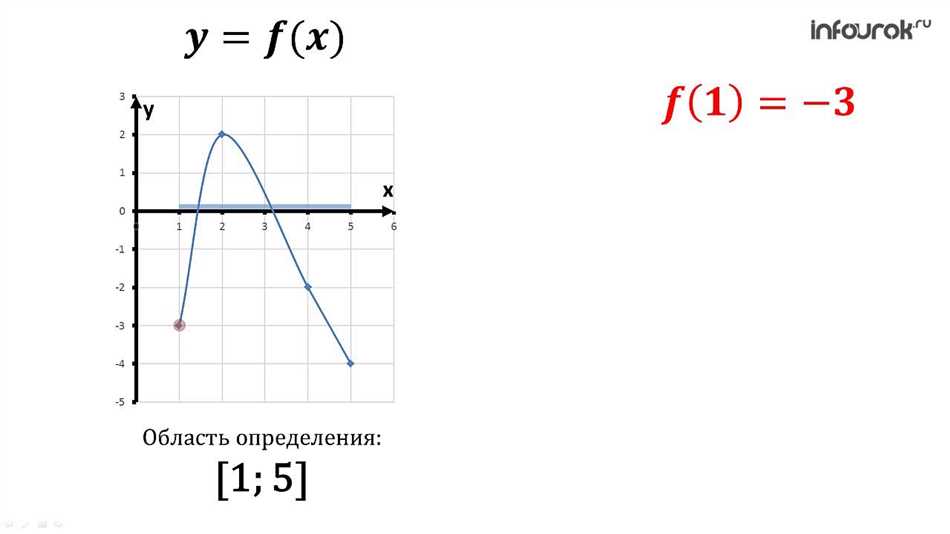
Значение функции — это результат вычисления функции, когда аргументы или переменные подставляются в функцию.
Например, рассмотрим функцию f(x) = x^2, где x — переменная. Если мы придаем переменной x значение 3, то мы можем вычислить значение функции следующим образом: f(3) = 3^2 = 9. Значение функции f(x) при x = 3 равно 9.
4. Значение уравнения
Значение уравнения — это значение переменной, которое удовлетворяет данному уравнению. Когда мы находим значение уравнения, мы находим значение переменной, которое делает уравнение истинным.
Например, рассмотрим уравнение 2x + 5 = 13. Чтобы найти значение x, мы решаем уравнение следующим образом: 2x + 5 = 13 — 5, 2x = 8, x = 8/2 = 4. Таким образом, значение уравнения 2x + 5 = 13, где x = 4, истинно.
В математике значение имеет важное значение, поскольку позволяет нам понять результаты вычислений, связи между переменными и выполнять различные операции. Значение помогает нам решать задачи, принимать решения и понимать мир вокруг нас.
Значение в контексте математических операций
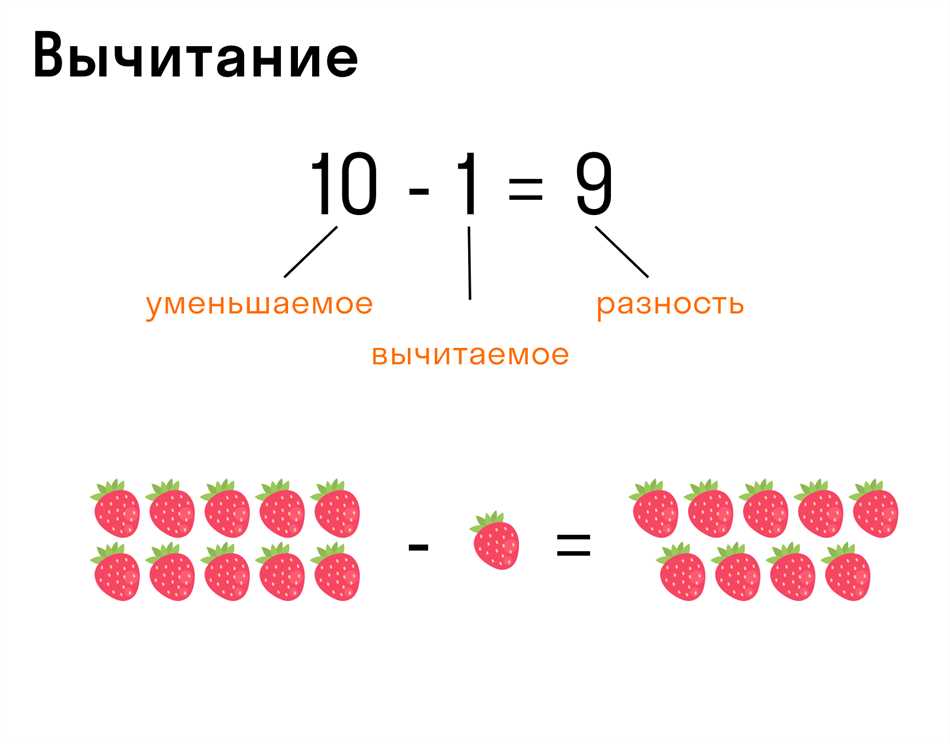
Значение в контексте математических операций — это численный результат, полученный в результате выполнения операции. Например, если мы сложим числа 5 и 3, получим значение 8. Если вычтем 3 из 5, получим значение 2. Значение может быть как положительным, так и отрицательным, в зависимости от характера операции и входных данных. Например, при умножении отрицательного числа на положительное число получим отрицательное значение, а при умножении положительного числа на положительное — положительное значение.
Значение в математических операциях может быть представлено как числом, так и физической величиной, такой как расстояние, площадь или объем. Например, при умножении длины прямоугольника на его ширину получим его площадь. Значение в этом случае будет представлено числом, которое указывает на размер площади в квадратных единицах.
Знание значения в контексте математических операций имеет огромное значение в реальной жизни. Представьте себе, что вы хотите посчитать общую стоимость товаров в своей корзине в интернет-магазине. Вам нужно будет умножить цену каждого товара на его количество и сложить все значения вместе, чтобы получить окончательную сумму. Если вы знаете значения математических операций, вы сможете точно рассчитать стоимость и быть увереными, что вы не переплатите или не упустите какие-либо важные детали.
Значение в математике: определение и примеры
Значение может быть числовым или символическим. Числовое значение получается, когда вместо переменных подставляются числа или конкретные значения. Например, в выражении 2x + 3, если подставить x = 5, получим значением 2 * 5 + 3 = 13.
Символическое значение содержит переменные или неопределенные значения, которые не были заменены на конкретные числа. Такое значение может быть полезно при проведении алгебраических операций или анализе уравнений и функций.
Примеры использования значения в математике:
- Вычисление значения функции при заданных значениях аргументов;
- Нахождение количественных решений уравнений;
- Проверка выполнения условий и неравенств;
- Определение границ и интервалов функций;
- Решение математических задач и применение математических моделей.