Когда мы говорим о физике, величины играют ключевую роль. Они являются основой для измерений и описания физических явлений. Величина — это физическая величина, которая может быть измерена и определена с помощью единицы измерения. Они используются, чтобы описать и объяснить различные явления, такие как скорость, масса, энергия и другие. Значение величины позволяет нам понять, как объекты и системы взаимодействуют, а также решить разнообразные задачи в физике. В этой статье мы рассмотрим определение и роль величины в физике, а также рассмотрим, почему они играют такую важную роль в нашем понимании мира.
Значение величины в физике
Значение величины в физике – это числовая характеристика, которая определяет, насколько большим или малым является этот параметр. Например, скорость – это физическая величина, которая показывает, на каком расстоянии объект перемещается за единицу времени.
Значение величины может быть как положительным, так и отрицательным. Например, если скорость объекта положительна, это означает, что он движется вперед. Если скорость отрицательна, то объект движется назад. Поэтому величины могут иметь разные значения в зависимости от направления движения объекта.
Значение величины играет важную роль в физике. Оно позволяет установить количественные соотношения между физическими явлениями и применить математические методы для их анализа. Без определенного значения величины, мы не смогли бы измерить или описать физические процессы.
Значение величины также позволяет сравнивать и классифицировать различные физические явления. Например, сравнивая значения мощности двух электрических приборов, мы можем определить, который из них потребляет больше энергии.
Чтобы определить значение величины, мы должны провести измерение с помощью специальных инструментов и методов. Например, для измерения скорости мы можем использовать спидометр, а для измерения массы – весы.
Важно отметить, что значение величины может быть абсолютным или относительным. Абсолютное значение описывает величину независимо от других параметров, например, абсолютная температура. Относительное значение указывает на отношение одной величины к другой, например, относительная влажность воздуха.
Хорошее понимание значения величины в физике позволяет нам лучше понять мир вокруг нас и использовать эту информацию для развития новых технологий и достижения новых научных открытий. А как часто мы задумываемся о том, сколько всего скрыто в цифрах и числах, которые описывают нашу реальность?
Определение величины
Определение величины может показаться простым, но после более детального рассмотрения оно открывает перед нами важные аспекты физического мира. Величины могут быть фундаментальными или производными, и все они играют свою роль в понимании нашей вселенной.
Фундаментальные величины, такие как масса, длина, время и электрический заряд, являются первичными и не могут быть выражены в терминах других величин. Они служат основой для определения других физических величин и использования их в уравнениях и законах.
Производные величины являются результатом комбинации фундаментальных величин и позволяют измерять и описывать различные аспекты физического мира. Примерами производных величин являются скорость, ускорение, сила, энергия и другие.
Значение величины является ключевым понятием в физике, потому что оно позволяет нам количественно оценить и описать различные явления и процессы. Например, измерение массы объекта позволяет нам оценить его количество вещества, а измерение времени — определить период или длительность какого-либо события.
Определение величины также играет важную роль в разработке и проверке физических теорий. Величины и их значения используются в уравнениях и формулах, которые описывают законы природы и позволяют предсказывать результаты экспериментов.
Функция величины в физике

В физике величина может рассматриваться как функция, которая описывает взаимосвязь между различными физическими явлениями. Функции величины используются для описания закономерностей, установления зависимостей или предсказания результатов экспериментов.
Физика изучает разнообразные феномены – от элементарных частиц до галактик во Вселенной. Чтобы понять и объяснить эти явления, физики используют функции, которые связывают величины и позволяют анализировать их взаимодействие. Например, закон Гука в механике описывает зависимость деформации упругого тела от приложенной силы и его упругих свойств. Это математическая функция, которая выражает эту взаимосвязь.
Функции величины могут быть простыми или сложными. Простые функции часто встречаются в основных физических законах, таких как законы Ньютона или закон Кулона. Они позволяют описать простые взаимодействия и приводят к простым математическим формулам. Но в некоторых случаях, особенно при изучении сложных систем, функции могут быть более сложными и требуют использования более сложных математических методов и моделей.
Таким образом, функции величины в физике играют важную роль в анализе и объяснении физических явлений. Они позволяют нам лучше понять мир вокруг нас и использовать это знание для создания новых технологий и развития науки.
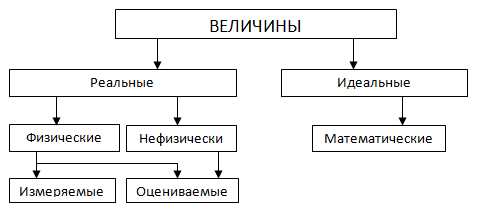
Виды величин
Поговорим о различных видах величин в физике. Когда мы изучаем физику, мы сталкиваемся с различными величинами, которые используются для измерения и описания физических явлений. Разные виды величин имеют свои особенности и свойства, которые дает нам возможность лучше понять мир вокруг нас.
Первый вид величин, с которым мы часто сталкиваемся, это фундаментальные величины. Они считаются базовыми для измерений и образуют основу для производных величин. Некоторые из таких фундаментальных величин включают в себя массу, время, длину и температуру. Фундаментальные величины нам дается понять с помощью конкретных единиц измерения, таких как кг, секунда, метр и градус Цельсия.
Следующий вид величин, о которых стоит упомянуть, это производные величины. Они образуются путем комбинирования фундаментальных величин. Производные величины позволяют нам описывать более сложные физические явления и связи между ними. Например, скорость — это производная величина, которая является отношением перемещения к затраченному времени. Производные величины могут быть измерены с помощью соответствующих единиц, таких как м/с для скорости или Н/м для силы.
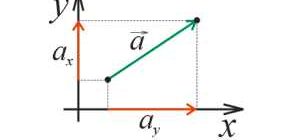
Третий вид величин, который стоит отметить, это векторные величины. Векторные величины имеют не только числовое значение, но также и направление. Например, сила и скорость — это векторные величины. Они могут быть представлены в виде стрелки, где длина стрелки представляет величину, а направление указывает на значение вектора. Векторные величины обычно используются для описания перемещения, силы и других физических величин.
Наконец, четвертый тип величин — это скалярные величины. В отличие от векторных величин, скалярные величины имеют только числовое значение и не имеют направления. Некоторые примеры скалярных величин включают в себя массу объекта, температуру и время. Скалярные величины измеряются просто с помощью соответствующих единиц, таких как кг для массы, градусы Цельсия для температуры и секунды для времени.
Итак, мы рассмотрели различные виды величин в физике. Фундаментальные величины, производные величины, векторные величины и скалярные величины предоставляют нам инструменты для изучения физических явлений и составляют основу нашего понимания мира. Использование этих различных видов величин позволяет нам более точно описать и измерить физические явления и связи между ними.
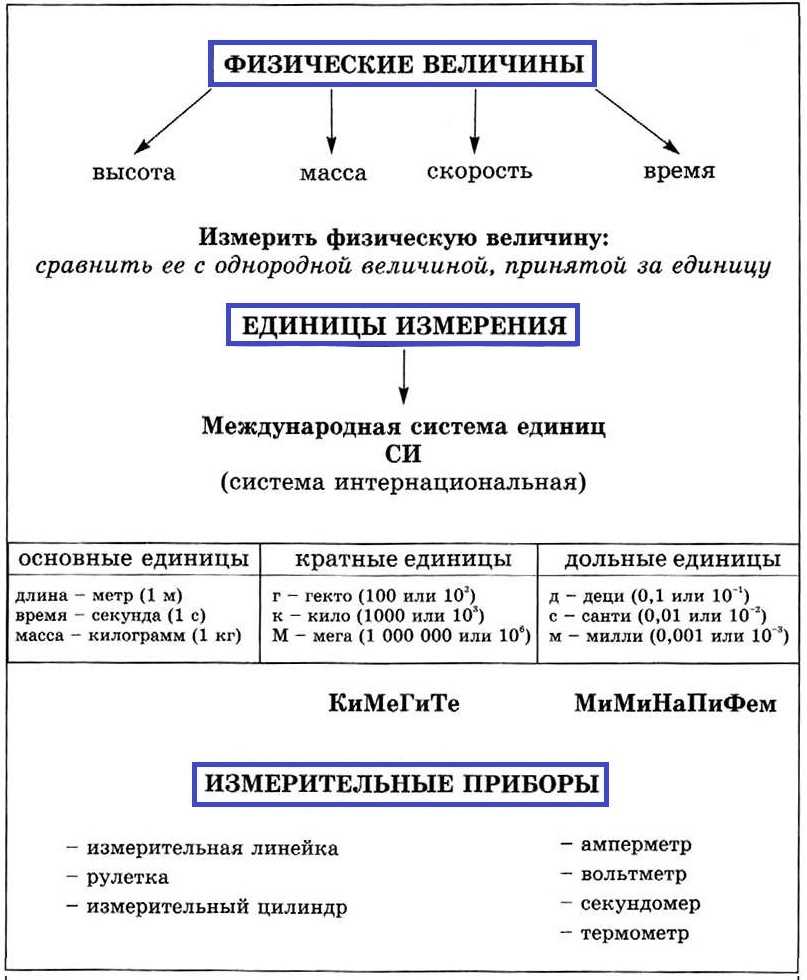
Физические величины

Физические величины делятся на две основные категории: базовые и производные. Базовые величины являются основой для измерения других величин и не могут быть выражены через другие величины. Примерами базовых величин являются длина, масса и время. Производные величины выражаются через базовые величины и представляют собой результат комбинации различных физических параметров. Например, скорость — это производная величина, которая указывает на изменение позиции объекта относительно времени.
Физические величины имеют большое значение в нашей повседневной жизни и они широко используются в различных областях, включая науку, инженерное дело и технологии. Мы осознанно или нет, используем физические величины, чтобы решать простые ежедневные задачи, например, измерять длину стола или время, проведенное в дороге.
Однако роль физических величин не ограничивается повседневными задачами. Они также играют важную роль в развитии науки и технологий. Физические величины позволяют нам создавать математическую модель реальных явлений и предсказывать результаты экспериментов. Они помогают нам понять физические законы и принципы, лежащие в основе всего сущего в нашей Вселенной.
Математические величины
Величины могут быть разделены на две категории: фундаментальные (основные) и производные. Фундаментальные величины включают в себя такие характеристики, как время, масса и длина. Эти величины не могут быть представлены в терминах других физических величин и являются основой для определения других производных величин. Например, скорость может быть определена как отношение изменения расстояния к изменению времени.
Производные величины, с другой стороны, определяются в терминах фундаментальных величин. Например, энергия может быть определена как произведение массы и квадрата скорости.
Величины в физике имеют также свои единицы измерения. Наиболее распространенные единицы измерения включают секунду (с) для времени, килограмм (кг) для массы, и метр (м) для длины. Они помогают нам измерять и сравнивать значения величин.
Зная значения величин и их единицы измерения, мы можем применять математические операции, такие как сложение, вычитание, умножение и деление, для получения новых значений и оценки физических связей между ними.
Математические величины играют важную роль в физике как в самых фундаментальных, так и в прикладных науках. Они позволяют нам представлять и понимать различные явления, проводить эксперименты и делать прогнозы. Без математических величин мы были бы ограничены в наших возможностях и понимании окружающего мира.
Роль величины в физике

Одна из ключевых ролей величин – определение и описание физических явлений. Физика стремится постичь законы и принципы природы, и величины помогают нам обратить внимание на различные аспекты физических процессов. Например, сила является основной величиной в механике и играет решающую роль в определении движения тела. Масса, температура, энергия – все это величины, которые помогают нам описать аспекты природы и понять ее законы.
Величины также играют важную роль в измерениях и экспериментах. С помощью измерения мы можем количественно оценить и сравнить различные физические величины. Например, измерение длины позволяет сравнить размеры разных объектов, а измерение времени помогает нам оценить длительность процессов.
Без величин физика была бы невозможна. Они являются основой для математического описания физических законов и принципов. Математика позволяет нам формализовать физические концепции и делает их строгими и точными. Величины являются основными объектами для математических моделей и уравнений, которые описывают поведение физических систем.
Также величины играют роль в практической области физики, такой как инженерия и технологии. Многие технологические процессы и устройства основаны на принципах физики и требуют точных измерений и расчетов физических величин. Например, величины как мощность, напряжение и электрический ток играют важную роль в электротехнике и электронике.
Величины в физике – это не только инструмент для описания, измерения и предсказания физических явлений, но и ключ к пониманию и взаимодействию с окружающим миром. Они помогают нам разобраться в том, как природа функционирует, и использовать этот знакомый язык для дальнейшего развития науки, технологий и нашей жизни в целом.
Измерение и вычисление величин
Измерение — это процесс определения значения величины в заданных единицах измерения. Оно позволяет нам получить количественную характеристику объекта или явления. Например, измерение длины маятника позволяет нам узнать его период колебаний.
Для измерения величин мы используем различные инструменты и приборы. Линейка позволяет измерить длину, весы — массу, термометр — температуру. Кроме того, величины могут измеряться с помощью более сложных приборов, таких как осциллограф или спектрометр.
Вычисление — это процесс получения новой величины на основе измеренных данных и математических операций. Простейшим примером вычисления является сложение двух чисел или умножение их на другие. В физике, вычисления могут быть более сложными и включать использование различных математических методов и формул.
Значение измеренной величины может быть выражено числовым значением и единицей измерения. Например, длина маятника может быть измерена в метрах, а его период колебаний — в секундах. Зачастую, величины можно измерять в разных единицах, и в этом случае необходимо использовать соответствующие формулы для перевода из одной системы единиц в другую.
Измерение и вычисление величин имеют огромное значение в физике. Они позволяют установить законы и принципы, описывающие физические явления, и создать математические модели для их объяснения и предсказания. Благодаря измерениям и вычислениям физики могут предсказывать поведение объектов в различных условиях и разрабатывать новые технологии и устройства.
Значение величины в физике: определение и роль
Значение величины описывает его интенсивность, количество или меру наличия в системе. Величины бывают различных типов: физические, химические, биологические и т. д. Каждая величина имеет определенные единицы измерения, которые указывают, как измерять или выражать эту величину.
Роль величин в физике тесно связана с проведением экспериментов, а также с разработкой и проверкой физических законов. Величины позволяют измерять и сравнивать объекты и явления, их свойства и параметры. Они служат основой для проведения математических расчетов, моделирования различных физических процессов и предсказания результатов экспериментов.
Величины в физике могут быть как базовыми, так и производными. Базовые величины являются фундаментальными и не могут быть выражены через другие величины. Некоторыми примерами базовых величин в физике являются масса, время, длина, заряд и температура. Производные величины получаются путем комбинации базовых величин и математических операций.
Точное и точнейшее измерение значений величин является важной составляющей экспериментальной работы в физике. Неверное определение значения величины или ее погрешность может привести к неверным результатам и неправильным интерпретациям экспериментальных данных. Поэтому физики придерживаются определенных методов и правил для проведения измерений и оценки погрешностей.
В целом, значение величины в физике играет ключевую роль в понимании и описании мира, помогает строить математические модели и разрабатывать физические законы, а также применять эти знания в практических приложениях и технологиях.