Основные понятия

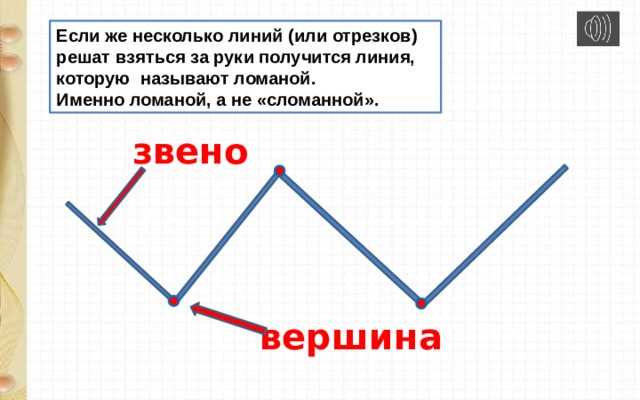
Простая ломаная — это ломаная, у которой все звенья не пересекаются между собой.
Замкнутая ломаная — это ломаная, у которой последнее звено соединяется с первым звеном, таким образом создавая замкнутую фигуру.
Выпуклая ломаная — это ломаная, у которой все внутренние углы являются острыми.
Вогнутая ломаная — это ломаная, у которой хотя бы один из внутренних углов является тупым.
Длина ломаной — это сумма длин всех ее звеньев.
Примеры:
- Простая ломаная: AB, BC, CD, DE.
- Замкнутая ломаная: AB, BC, CD, DA.
- Выпуклая ломаная: AB, BC, CD, DE.
- Вогнутая ломаная: AB, BC, CD, DE.
Важно понимать и уметь применять эти основные понятия на практике, так как они являются основой для изучения более сложных концепций и тем в геометрии.
Ломаная
Здравствуй, дорогой читатель! Позволь мне ввести тебя в захватывающий мир математики. Сегодня мы поговорим о ломаной. Что это такое? Как она выглядит? И как ее можно использовать в повседневной жизни?
Ломаная — это геометрическая фигура, состоящая из последовательности отрезков, которые соединяют точки на плоскости. Каждый отрезок называется звеном ломаной. Захватывающе, правда?
Давай представим, что ты идешь по улице, а на тротуаре нарисована странная фигура из прямых линий. Вот это и есть ломаная! Она может быть изогнутой, иметь различную форму и повернута в разных направлениях. Она может быть длинной или короткой, разделенной на разные участки или состоять из одного отрезка. Ломаная — это настоящий геометрический хаос, который можно понять и привести в порядок.
Зачем же нам нужны ломаные в повседневной жизни? Ответ очень простой — они помогают нам анализировать и представлять данные. Ломаная может быть использована для отображения различных процессов и изменений величин. Например, если ты хочешь представить изменение температуры в течение дня или доход компании за год, можно использовать ломаную. Кроме того, она может быть полезна для построения графиков и решения различных математических задач.
Теперь, когда мы познакомились с понятием ломаной, давайте рассмотрим некоторые ее особенности. Ломаная может быть замкнутой или разомкнутой. Если первая и последняя точки ломаной совпадают, то она замкнута, иначе — разомкнута. Также, ломаная может быть прямой или наклонной. Если все звенья ломаной расположены на одной прямой, она будет прямой. В противном случае, ломаная будет наклонной.
Итак, ломаная — это замечательный инструмент для представления данных и решения задач. Она позволяет нам увидеть изменения, происходящие вокруг нас, и легко анализировать информацию. Попробуй сам нарисовать ломаную и поиграть с ее формой. Кто знает, может быть, ты сможешь открыть для нас что-то новое и удивительное!
Звено: ключевое понятие в ломаной линии
Давай представим, что ломаная линия – это цепочка, состоящая из нескольких звеньев. Каждое звено имеет свою особенность и смысл, и они вместе формируют всю ломаную линию.
Например, давай посмотрим на три звена, которые образуют ломаную линию:
- Первое звено – это начальная точка ломаной линии. Она определяет, с какого места мы начинаем построение линии.
- Второе звено – это промежуточная точка между начальной и конечной точками. Оно определяет, как ломаная линия будет вести себя между двумя точками.
- Третье звено – это конечная точка, к которой ломаная линия стремится. Она завершает линию и определяет ее конечный результат.
Теперь давай применим эти знания на практике. Представь себе, что ты строишь дорожку для игровой машинки. Начальная точка (первое звено) – это твое место старта, промежуточные точки (вторые звенья) – это клетки, через которые проходит твоя машинка, и конечная точка (третье звено) – это финишная линия, которую твоя машинка должна достичь.
Таким образом, знание о звеньях позволяет нам легче понять, как устроена ломаная линия и как она влияет на наш результат. Использование звеньев помогает нам строить правильные геометрические фигуры и решать математические задачи.
Так что, пользуйся своим знанием о звеньях и строй не только дорожки для игрушек, но и успешные карьерные пути, красивые рисунки и интересные математические решения. Уверен, ты справишься!
Примеры звеньев ломаной
- Допустим, у нас есть ломаная линия, которая состоит из трех звеньев. Первое звено — это отрезок от точки А до точки В. Второе звено — от точки В до точки С. И третье звено — от точки С до точки Д.
- В другом примере у нас может быть ломаная линия с более чем тремя звеньями. Например, первое звено — от точки А до точки Б, второе звено — от точки Б до точки С, третье звено — от точки С до точки Д, четвертое звено — от точки Д до точки Е и так далее.
- Иногда звенья ломаной не имеют физического представления и используются для абстрактного представления данных. Например, в математических графиках звенья ломаной могут представлять значение функции на разных точках.
Важно помнить, что звенья ломаной могут быть как прямолинейными, так и кривыми. Они могут быть горизонтальными, вертикальными и даже диагональными.
Что вы думаете о звеньях ломаной? Можете ли вы найти еще примеры звеньев ломаной в повседневной жизни? Расскажите свои мысли!
Звено-отрезок: основные понятия и примеры
Звено-отрезок — это часть ломаной линии, которая соединяет две соседние вершины, т.е. две соседние точки на плоскости. Можно сказать, что звено-отрезок — это отрезок ломаной линии, который включает в себя две соседние точки и все точки, лежащие между ними.
Давай рассмотрим пример, чтобы лучше понять, что такое звено-отрезок. Представь себе ломаную линию, на которой расположены пять точек: A, B, C, D и E. Звено-отрезком в этом случае будет отрезок, который соединяет соседние точки. Например, звено-отрезок AB будет включать в себя точки A и B, а также все точки, которые находятся между ними.
Важно отметить, что звено-отрезки имеют разную длину. Например, звено-отрезок CD может быть короче, чем звено-отрезок AB. Здесь нет строгих ограничений, и длина каждого звена-отрезка зависит от конкретной ломаной линии.
Теперь, когда мы разобрались с понятием звено-отрезка, можешь попробовать найти их вокруг себя. Взгляни на окружающие предметы или картину и попробуй описать ломаную линию, соединяющую соседние точки. Таким образом, ты сможешь увидеть звенья-отрезки и понять, как они образуют ломаную линию.
Надеюсь, что сейчас тебе стало ясно, что такое звено-отрезок и как оно связано с ломаной линией. Запомни, что звено-отрезок это часть ломаной линии, которая соединяет две соседние точки. Продолжай изучать геометрию и искать звенья-отрезки вокруг себя. Удачи!
Звено-луч
Давайте представим себе, что мы имеем два отрезка: один отрезок начинается в одной точке и оканчивается в другой, а второй отрезок начинается во второй точке и оканчивается в третьей точке. Вот эти два отрезка и образуют звено-луч.
Важные аспекты понятия «Звено-луч»
- Звено-луч имеет только две конечные точки.
- Звено-луч может быть прямым или кривым.
- Звено-луч не имеет промежуточных точек.
- Звено-луч является составной частью ломаной линии.
Итак, звено-луч – это связующее звено между двумя отрезками на плоскости, которые идут из одной точки в другую. Звено-луч образует четкую и неразрывную связь между отрезками и является важной составляющей ломаной линии.
Звено-луч можно легко представить себе, визуализируя его на плоскости. Представьте себе стрелку, которая указывает на определенную точку – это будет звено-луч. А теперь представьте стрелки, указывающие на разные точки, и их связующие – это уже будет ломаная линия.
Звено-луч – это ключевое понятие в изучении ломаных линий. Оно помогает нам понять, как разные отрезки образуют связную и непрерывную линию. Звено-луч дает нам возможность легко визуализировать и анализировать ломаные линии, делая из них более понятные и доступные для изучения.
Звенья ломаной 5 класс: основные понятия и примеры

Важными понятиями ломаных являются:
- Вершина — точка пересечения двух звеньев.
- Начало и конец ломаной — точки, которые являются началом и концом самой ломаной.
- Отрезок ломаной — звено, которое соединяет две соседние вершины ломаной.
Примеры звеньев ломаной:
- Прямолинейное звено — отрезок прямой ломаной, который соединяет две вершины линейно.
- Криволинейное звено — отрезок кривой ломаной, который соединяет две вершины, образуя изгиб или излом.
| Тип звена | Пример |
|---|---|
| Прямолинейное звено | Отрезок AB |
| Криволинейное звено | Дуга BC |