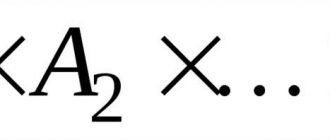
Если ты учишься в пятом классе и изучаешь математику, то ты, наверняка, уже знаком с понятием «ломаная». В математике звенья ломаной — это отрезки, которые соединяют точки. Изучение этой темы поможет тебе развить свои навыки в геометрии. Звенья ломаной могут быть прямыми или кривыми, они могут иметь разную длину и форму. Учись строить ломаную, определять ее вид и свойства. Это очень полезные навыки, которые пригодятся тебе не только в школе, но и в жизни. Давай разберемся вместе!
Понятие ломаной
Здравствуй, друг! Сегодня мы поговорим о звеньях ломаной. Ты когда-нибудь задумывался, как узнать, что представляет собой ломаная? Мы могли бы просто определить ее как линию, которая состоит из нескольких звеньев или отрезков. Но давай погрузимся глубже.
Ломаная – это геометрическая фигура, состоящая из прямых отрезков. Но самое интересное, что эти отрезки не обязательно должны быть в одной и той же прямой линии. Они могут быть разнонаправленными и образовывать углы. Таким образом, ломаная является некоторой последовательностью отрезков, которые могут сворачивать и менять направление.
Смотри, когда мы говорим о звеньях ломаной, мы имеем в виду отрезки, из которых она состоит. Звенья ломаной могут быть прямолинейными или криволинейными, они могут быть одинаковой длины или разной. Именно эти звенья и создают форму ломаной, делают ее разнообразной и уникальной.
Как ты можешь использовать понятие ломаной в повседневной жизни? Давай представим, что ты хочешь построить необычную дорожку в своем саду. Ты можешь использовать ломаную форму, чтобы создать интересный и оригинальный путь. Сгниют знаешь, ломаная также используется в архитектуре и дизайне для создания красивых и эстетических композиций.
Итак, вот ответ на твой вопрос о понятии ломаной. Она представляет собой геометрическую фигуру, состоящую из прямых отрезков, которые могут сворачивать и менять направление. Звенья ломаной могут быть разного вида и длины, что делает ее уникальной и интересной. Ты можешь использовать понятие ломаной в своей повседневной жизни для создания необычных и красивых объектов или композиций.
Определение ломаной
Возьмем, к примеру, карту. Представь, что ты хочешь пройти по ней от одного места к другому. Но перед тем, как приступить к путешествию, ты решил нанести на карту путь, который будешь следовать. Для этого ты начал проводить прямые линии от одного места к другому, каждый раз меняя направление. В итоге, ты получил некую фигуру, которую называют ломаной.
Интересно, что ломаные встречаются не только на картах. Мы можем встретить их в реальной жизни. Например, деревья, реки, горы и даже наши траектории движения могут быть описаны ломаными.
Ломаная может быть замкнутой или разомкнутой. Замкнутая ломаная начинается и заканчивается в одной и той же точке, а разомкнутая – в разных.
Теперь, когда мы знаем, что такое ломаная, давай посмотрим, как мы можем использовать ее для решения задач.
Примеры ломаных
Рассмотрим несколько примеров ломаных:
1. Простая замкнутая ломаная:
- Возьмем три отрезка разной длины.
- Соединим конец первого отрезка с началом второго отрезка.
- Соединим конец второго отрезка с началом третьего отрезка.
- И наконец, соединим конец третьего отрезка с началом первого отрезка, чтобы получить замкнутую фигуру.
 |
Замкнутая ломаная |
2. Ломаная с пересечениями:
- Возьмем четыре отрезка разной длины.
- Соединим конец первого отрезка с началом второго отрезка.
- Соединим конец второго отрезка с началом третьего отрезка.
- Соединим конец третьего отрезка с началом четвертого отрезка.
- Соединим конец четвертого отрезка с началом первого отрезка.
- В результате получим фигуру с двумя пересечениями в углах.
 |
Ломаная с пересечениями |
3. Скругленная ломаная:
- Возьмем несколько отрезков разной длины.
- Соединим конец первого отрезка с началом второго отрезка.
- Соединим конец второго отрезка с началом третьего отрезка.
- Но вместо прямого угла, создадим скругление внутри каждого угла.
- Итоговая фигура будет иметь закругленные углы.
 |
Скругленная ломаная |
Это лишь некоторые примеры ломаных. В математике существует множество других интересных и сложных ломаных, которые могут быть использованы для создания разнообразных геометрических фигур и графиков. Ломаные имеют множество применений в реальной жизни, например, в архитектуре, дизайне и технике. Так что не стесняйтесь экспериментировать и создавать свои собственные ломаные!
Свойства звеньев ломаной
Первое свойство звеньев ломаной – их сумма равна длине ломаной. Если мы сложим все звенья, получим длину всей ломаной. Представьте, что каждое звено – это кусочек нити, и если их аккуратно сложить один за другим, получится нужная длина. Это логично, ведь каждое звено просто является отрезком на линии, которая образует ломаную.
Второе свойство – длина каждого звена меньше суммы длин ломаной от него до предыдущего звена и от него до следующего звена. Например, если мы возьмём любое звено и измерим расстояние от него до предыдущего и до следующего звена по линии ломаной, то это расстояние будет больше, чем само звено. Это просто объясняется тем, что звено часть линии, и линия всегда будет длиннее отрезка, который является её частью.
Третье свойство – длина каждого звена меньше суммы длин соседних звеньев. Если мы возьмём любые два соседних звена ломаной и измерим их длины, то каждая из них будет меньше суммы длин обоих звеньев. Этот факт следует из предыдущего свойства и можно наглядно представить, нарисовав звенья вместе.
И последнее, четвёртое свойство – длина каждого звена меньше суммы длин всех звеньев после него. Например, если мы возьмём звено и измерим длину каждого последующего звена и сложим все эти длины, то получим сумму длин всех звеньев после данного звена. Данное свойство также следует из предыдущих свойств и можно представить, нарисовав все звенья ломаной.
Важно запомнить эти свойства звеньев ломаной, так как они помогут нам лучше понять и использовать геометрические фигуры и решать задачи с их участием. Изучайте материал с интересом и радуйтесь своим успехам!
Звенья ломаной
Звенья ломаной могут быть разной длины и направления. Например, первое звено может быть длиннее второго звена, а третье звено может быть направлено в противоположную сторону. Все эти различия определяют форму и структуру ломаной.
Ломаная может иметь разное количество звеньев. Она может быть составлена из трех звеньев, пяти звеньев, десяти звеньев и так далее. Количество звеньев в ломаной определяет ее длину и сложность.
Знание о звеньях ломаной важно в различных областях математики, таких как геометрия, алгебра и анализ. Оно помогает нам анализировать и работать с графиками, координатными плоскостями, уравнениями и многими другими математическими концепциями.
Например, при работе с графиками функций мы можем представить функцию в виде ломаной, составленной из отрезков. Каждое звено ломаной будет соответствовать значению функции в определенной точке. Это позволяет нам визуализировать и анализировать свойства и поведение функции на графике.
Также знание о звеньях ломаной может быть полезно при решении задач по геометрии. Мы можем использовать ломаную, чтобы представить сложные фигуры и выполнять операции по их анализу, например, находить периметр или площадь.
Таким образом, понимание звеньев ломаной играет важную роль в математике. Это помогает нам анализировать и визуализировать различные математические концепции, такие как функции и геометрические фигуры. Независимо от того, в какой области математики вы работаете, знание о звеньях ломаной может быть полезным инструментом.
Соединение звеньев: путь к логическому мышлению
Соединение звеньев — это как головоломка, которую нужно разгадать. Но самое интересное в этом процессе — развитие логического мышления. Когда мы соединяем звенья, мы сталкиваемся с вопросами о направлении, порядке и промежуточных точках. И это требует от нас аналитического подхода и способности видеть картину в целом.
Представь, что ты в качестве архитектора создаешь план здания. Ты должен быть внимателен и точен, чтобы все соединения были правильными и держались крепко. В итоге, ты создаешь прекрасную структуру, в которой все звенья слаженно сливаются в единое целое. Именно так и работает математика — каждое звено соединяется с другим и создает гармоничный образ.
Также, соединение звеньев помогает нам узнавать и понимать новые математические понятия. Когда мы экспериментируем с разными способами соединения, мы обнаруживаем закономерности и законы, которые можно применять в других ситуациях. Это как пазл, где каждое звено — это кусочек большой картинки, и когда мы правильно соединяем звенья, мы видим весь образ.
Но ведь математика — не только о формах и структурах. Она помогает развивать наше мышление, находить решения, учиться анализировать и синтезировать информацию. Соединение звеньев — это лишь один из способов, которым мы можем проявить наше творчество и способности мыслить абстрактно.
Так что не бойся экспериментировать и соединять звенья. Ведь именно в этом процессе ты развиваешь свои математические и логические навыки, становишься умнее и увереннее. А когда у тебя получится создать красивую и правильную ломаную, ты почувствуешь себя настоящим художником математики!
Построение ломаной
Как же строить ломаную? Это достаточно просто! Для начала, нам нужно иметь точки, которые будут являться вершинами ломаной. Затем, мы соединяем эти точки отрезками. Но как выбрать нужные точки и насколько эти отрезки должны быть длинными?
Ответ на эти вопросы зависит от конкретной задачи, которую мы решаем. Например, если нам нужно построить ломаную, пройдя через определенные точки на координатной плоскости, мы можем использовать информацию о значениях этих точек. Мы можем начать строить ломаную, начиная с первой точки и соединяя ее с последующими точками путем отрезков. В результате, получится ломаная, проходящая через все заданные точки.
Важно помнить, что построение ломаной может быть связано с некоторыми условиями или ограничениями. Например, в некоторых задачах мы можем строить ломаную только вертикальными и горизонтальными отрезками. В таких случаях, мы должны выбирать точки так, чтобы линии между ними были перпендикулярными или параллельными осям координат.
Иногда, мы можем строить ломаную с помощью графических методов. Например, если у нас есть точки, находящиеся на одной прямой, мы можем использовать линейку и карандаш, чтобы нарисовать отрезки, соединяющие эти точки. Таким образом, мы постепенно будем строить линию, которая будет приближаться к ломаной.
Построение ломаной — это интересный способ визуализации и работы с геометрическими фигурами. Оно позволяет представить сложные задачи и решения в простой и наглядной форме. Более того, создание ломаной может стимулировать наше творческое мышление и развивать навыки работы с пространственными отношениями.
Построение ломаной на координатной плоскости
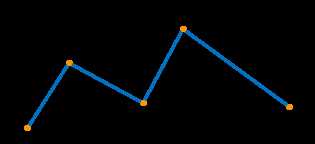
Давайте представим себе следующую ситуацию: у нас есть точки на плоскости, и мы хотим соединить их линиями для получения ломаной. Как это сделать? Прежде всего, нам нужно определить координаты каждой точки и запомнить их. Затем мы можем начать соединять точки отрезками, следуя порядку, заданному условием.
Для начала давайте рассмотрим пример. Предположим, у нас есть три точки на плоскости с координатами:
- Точка A: (2, 4)
- Точка B: (5, 6)
- Точка C: (7, 2)
Наша задача — соединить эти точки линиями для построения ломаной. Прежде всего, нарисуем оси координат и пометим точки на плоскости:
| x | y | |
|---|---|---|
| Точка A | 2 | 4 |
| Точка B | 5 | 6 |
| Точка C | 7 | 2 |
Теперь мы можем начать соединять точки отрезками. Начнем с соединения точек A и B:
Вопрос: какие будут координаты промежуточной точки между A и B?
Для ответа на этот вопрос нам нужно использовать знания о промежуточных значениях между двумя числами. В данном случае, промежуточная точка будет находиться между x-координатами точек A и B, и y-координата будет находиться между y-координатами точек A и B.
В нашем примере, промежуточная точка между A и B будет иметь координаты:
- x: (2 + 5) / 2 = 3.5
- y: (4 + 6) / 2 = 5
Таким образом, промежуточная точка между A и B будет иметь координаты (3.5, 5). Мы можем провести отрезок между A и B через эту промежуточную точку.
Затем мы можем продолжить соединять оставшиеся точки, следуя этому же принципу. Соединяем B и C:
Вопрос: какие будут координаты промежуточной точки между B и C?
Промежуточная точка будет иметь координаты, равные средним значениям x-координат и y-координат точек B и C. В нашем примере:
- x: (5 + 7) / 2 = 6
- y: (6 + 2) / 2 = 4
Таким образом, промежуточная точка между B и C будет иметь координаты (6, 4). Мы можем провести отрезок между B и C через эту промежуточную точку.
И наконец, мы можем соединить A и C:
Вопрос: какие будут координаты промежуточной точки между A и C?
Промежуточная точка будет иметь координаты, равные средним значениям x-координат и y-координат точек A и C. В нашем примере:
- x: (2 + 7) / 2 = 4.5
- y: (4 + 2) / 2 = 3
Таким образом, промежуточная точка между A и C будет иметь координаты (4.5, 3). Мы можем провести отрезок между A и C через эту промежуточную точку.
Итак, мы соединили все три точки отрезками и получили ломаную на координатной плоскости. Задача выполнена успешно!
Когда мы умеем строить ломаную на координатной плоскости, мы можем использовать этот навык для решения задач и проблем в математике. Например, мы можем определить длину ломаной, найти промежуточные значения функции или найти самую короткую дистанцию между двумя точками на плоскости.
Важно помнить, что построение ломаной на координатной плоскости требует точных вычислений и умения работать с координатами. Ответы на приведенные выше вопросы могут быть разными в разных случаях, поэтому важно понимать принципы и основы работы с ломаными.
Надеюсь, что этот пример помог вам лучше понять, как построить ломаную на координатной плоскости. Практикуйтесь в этом навыке, и вы сможете легко справиться со множеством задач и проблем в математике!
Звенья ломаной в математике 5 класс
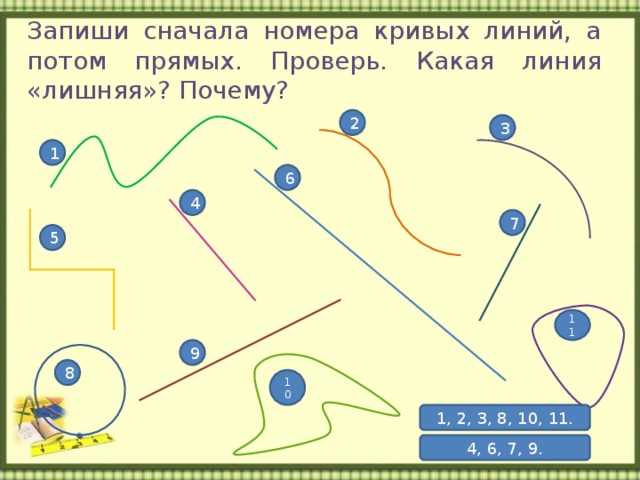
В математике звенья ломаной используются для изучения пространственных и графических представлений объектов. Ломаная можно представить как последовательность звеньев, которые соединяют вершины.
Звенья ломаной могут быть разной длины и формы. Они могут быть прямыми или изогнутыми. В зависимости от своего расположения, звенья ломаной могут принимать разные относительные положения друг к другу.
При изучении звеньев ломаной важно учитывать их последовательность. Изменение порядка звеньев может привести к изменению формы и структуры ломаной.
Для более наглядного представления звеньев ломаной можно использовать таблицу, в которой каждой вершине будет соответствовать номер. В таблице можно указать координаты каждой вершины и длину каждого звена.
Например, рассмотрим ломаную с вершинами A(1,2), B(3,4) и C(5,6). Расстояние между вершинами может быть вычислено по формуле: √((x2-x1)^2 + (y2-y1)^2).
| Вершина | Координаты | Длина звена |
|---|---|---|
| A | (1,2) | — |
| B | (3,4) | √((3-1)^2 + (4-2)^2) = √8 |
| C | (5,6) | √((5-3)^2 + (6-4)^2) = √8 |
Таким образом, звенья ломаной могут быть представлены математически и использоваться для анализа различных взаимосвязей и закономерностей в геометрии и графике.