Компланарные векторы в геометрии: основные понятия и свойства

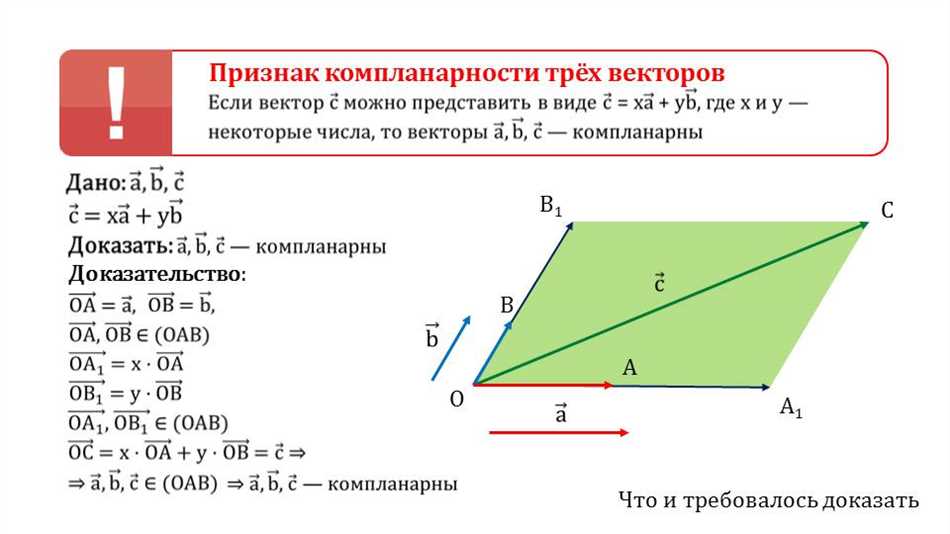
В геометрии существует понятие компланарных векторов, которые лежат в одной плоскости и имеют общую начальную точку. Рассмотрим различные свойства этих векторов, которые позволяют нам легче работать с ними и решать геометрические задачи.

Первое свойство компланарных векторов заключается в том, что они могут быть представлены как линейная комбинация других векторов, лежащих в той же плоскости. Это позволяет нам выражать один вектор через другие и находить их сумму или разность.

Еще одно важное свойство — компланарные векторы могут быть коллинеарными, то есть лежать на одной прямой. Это означает, что один вектор может быть умножен на скаляр, чтобы получить другой вектор.

Знание свойств компланарных векторов помогает нам решать различные задачи, связанные с геометрией и аналитической геометрией, а также находить решения векторных уравнений и определять геометрическую форму объектов.

Основное понятие компланарности векторов

Для того чтобы понять, являются ли векторы компланарными или нет, можно использовать геометрический подход. Если векторы представлены в виде направленных отрезков, то можно нарисовать их концы на плоскости и посмотреть, могут ли они быть соединены прямыми линиями внутри этой плоскости.

Также, можно использовать алгебраический подход. Если векторы представлены в виде координат, то можно записать их координаты в виде матрицы и посмотреть, имеют ли эти векторы ненулевые линейные комбинации, которые равны нулевому вектору. Если такие комбинации существуют, то векторы являются компланарными.

Одним из примеров компланарных векторов является векторная сумма двух или более векторов, которые лежат на одной прямой. В этом случае, все эти векторы лежат на одной плоскости, так как прямая может быть рассмотрена как ось этой плоскости.

Компланарные векторы имеют множество применений в геометрии и физике. Например, они используются для описания движения тела в трехмерном пространстве, так как позволяют определить положение и направление объекта на плоскости. Также, определение компланарности векторов позволяет упростить математические вычисления и решение задач, связанных с векторами.

Определение компланарности векторов

Когда мы говорим о компланарности векторов, мы имеем в виду их расположение в трехмерном пространстве.

Векторы называются компланарными, если они лежат в одной плоскости. Плоскость в этом случае является афинной оболочкой векторов, то есть она проходит через все эти точки, заданные векторами.

Для того чтобы понять, являются ли данные векторы компланарными или нет, можно применить следующий метод. Нужно найти векторное произведение между данными векторами. Если векторное произведение равно нулю, то векторы компланарны.

Иначе говоря, векторы a и b компланарны, если определитель матрицы, построенной на основании этих векторов, равен нулю:

a × b = 0

Здесь a × b обозначает векторное произведение векторов a и b.

То есть, когда векторное произведение двух векторов равно нулю, это означает, что либо вектора коллинеарны и лежат на одной прямой, либо они компланарны и лежат в одной плоскости. В данном случае речь идет о компланарности.

Компланарность векторов имеет важное значение в различных областях, таких как физика, геометрия и инженерное дело. Например, в механике компланарные векторы используются для решения задач, связанных с равновесием и движением твердых тел.

Векторы, которые не являются компланарными, называются некомпланарными. В этом случае они не лежат в одной плоскости, а расположены в трехмерном пространстве таким образом, что нельзя изобразить их на одной плоскости без пересечения.

Примеры компланарных и некомпланарных векторов

Компланарные векторы:

Примером компланарных векторов может служить сила тяжести и сила, приложенная к верхней точке нитью. Если представить тело, связанное с нитью, как плоскую фигуру, то направление силы тяжести, направленной вниз, и силы натяжения нити, направленной вверх, будут лежать на одной плоскости.

Еще одним примером компланарных векторов может быть сила трения и суммарная сила, действующая на объект. Если представить объект, лежащий на горизонтальной поверхности, то направление силы трения и суммарные силы, состоящие из силы тяжести и силы, приложенной к объекту, будут также лежать на одной плоскости.

Некомпланарные векторы:

Примером некомпланарных векторов может служить сила тяжести и сила, приложенная к боковой стороне объекта. Если представить объект, на котором действуют эти силы, то направления силы тяжести, направленной вниз, и силы, приложенной к боковой стороне, будут лежать в разных плоскостях.

Еще одним примером некомпланарных векторов может быть скорость движения объекта и сила, направленная вдоль оси вращения объекта. Если рассмотреть объект, вращающийся вокруг некоторой оси, то вектор скорости движения объекта и вектор силы, направленной вдоль оси вращения, будут находиться в разных плоскостях.

Таким образом, компланарные векторы являются векторами, которые лежат в одной плоскости, тогда как некомпланарные векторы находятся в разных плоскостях.

Свойства компланарных векторов

1. Объединение компланарных векторов

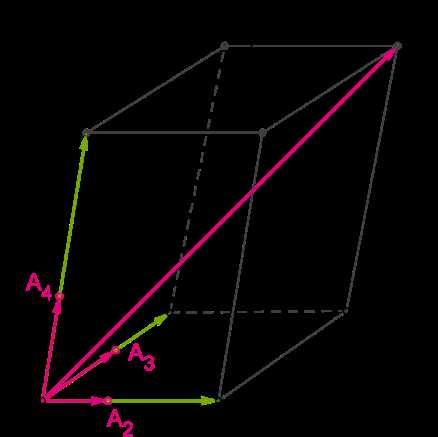
Когда компланарные векторы объединены началами, получается новый вектор с началом в том же месте и концом в той же плоскости, где находятся исходные векторы. Это свойство позволяет нам выполнять операции с компланарными векторами, такие как сложение или вычитание.

2. Пропорциональные компланарные векторы

Если два вектора компланарны и пропорциональны друг другу, то они также лежат в одной плоскости. Это означает, что можно умножить один вектор на число, чтобы получить другой вектор.

3. Линейная комбинация компланарных векторов

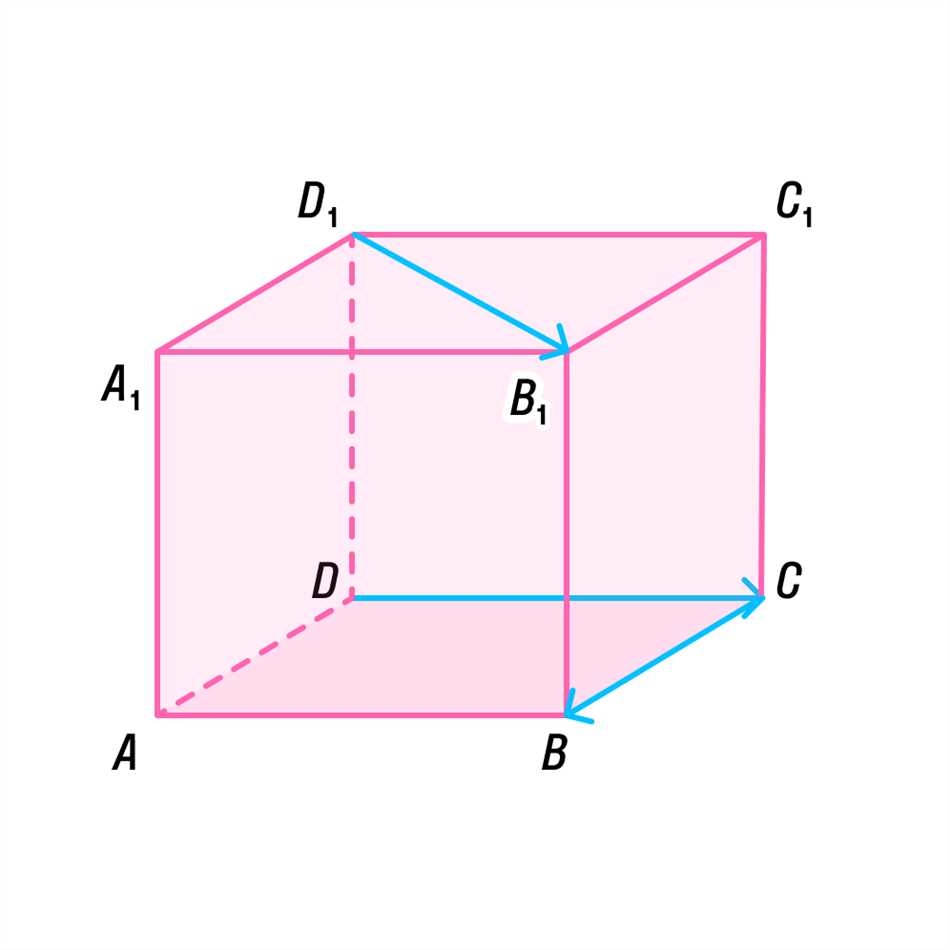
Линейная комбинация компланарных векторов — это сумма или разность векторов, умноженная на число. Если векторы компланарны, то их линейная комбинация также будет лежать в той же плоскости. Это свойство помогает нам работать с компланарными векторами при решении геометрических задач.

4. Перпендикулярный вектор

Если вектор перпендикулярен к плоскости, содержащей компланарные векторы, то он будет перпендикулярен каждому из этих векторов. Это свойство помогает нам определить, является ли вектор перпендикулярным к данной плоскости.

5. Формула смешанного произведения

Смешанное произведение компланарных векторов можно использовать для нахождения объема параллелепипеда, образованного этими векторами. Формула смешанного произведения позволяет нам выразить этот объем через модуль смешанного произведения векторов.

Свойства компланарных векторов играют важную роль в геометрии и помогают нам анализировать и использовать векторы в плоскостях. Знание этих свойств позволяет лучше понять геометрические задачи и решать их более эффективно.

Сложение компланарных векторов

Сложение компланарных векторов происходит по следующему правилу: для получения результирующего вектора необходимо сложить соответствующие компоненты данных векторов. Если у нас есть два вектора A = (a₁, a₂, a₃) и B = (b₁, b₂, b₃), то результирующий вектор C = (c₁, c₂, c₃) вычисляется следующим образом:

• Координата c₁ результирующего вектора равна сумме координат a₁ и b₁.
• Координата c₂ результирующего вектора равна сумме координат a₂ и b₂.
• Координата c₃ результирующего вектора равна сумме координат a₃ и b₃.

Таким образом, сложение компланарных векторов является простой и понятной операцией. Важно помнить, что сложение векторов коммутативно, то есть порядок слагаемых не влияет на результат. Также векторы можно складывать по частям, то есть сначала сложить два вектора, затем результат сложения добавить к третьему вектору и так далее.

Сложение компланарных векторов имеет множество практических применений в различных областях, включая физику, инженерию, компьютерную графику и многие другие. Например, в физике сложение векторов используется для определения силы, действующей на тело, а в компьютерной графике — для построения трехмерных моделей и анимаций.

Тема: Компланарные векторы в геометрии: понятие и свойства

Основное свойство компланарных векторов заключается в том, что они могут быть линейно выражены друг через друга.

Свойства компланарных векторов:

1. Компланарные векторы могут быть сложены между собой.
2. Компланарные векторы могут быть умножены на скаляры.
3. Компланарные векторы могут быть линейно выражены друг через друга.
4. Компланарные векторы могут образовывать треугольник или параллелограмм, который лежит в той же плоскости.
5. Система векторов является компланарной, если ее ранг меньше или равен 2.

Компланарные векторы широко применяются в геометрии, физике, аэродинамике, компьютерной графике и других областях. Они позволяют решать различные задачи, связанные с расчетами плоскостей, движением тел в пространстве и многими другими.