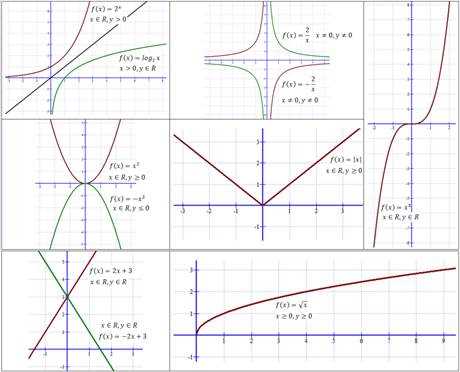
Когда мы говорим о функциях в алгебре, мы обычно имеем в виду определенное множество значений, которые функция может принимать. Это множество, называемое областью определения функции, определяет, какие входные значения могут быть использованы для функции и что они могут представлять. Область определения функции может быть ограничена различными условиями и ограничениями, которые определяют допустимые значения для функции.
Определение функции
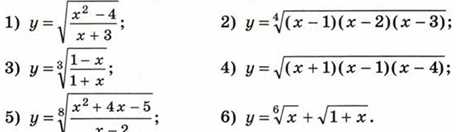
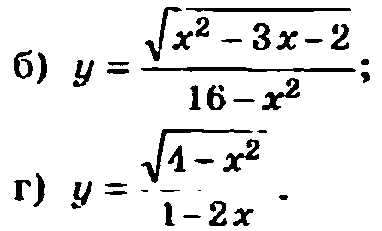
Определение функции включает в себя несколько ключевых элементов. Во-первых, у функции должно быть множество возможных входных данных, которое называется областью определения. Это множество определяет, какие значения можно подставлять в функцию. Например, функция «f(x) = x^2» имеет область определения всех действительных чисел.
Во-вторых, функция должна быть определена для каждого значения из области определения. Это означает, что для каждого возможного входного значения функция должна возвращать результат. В противном случае, если для какого-то значения функция не определена, говорят, что функция не существует.
Например, если рассмотреть функцию «g(x) = 1/x», то ее область определения включает все значения, кроме нуля, так как нельзя делить на ноль. Это означает, что функция определена для всех действительных чисел, кроме нуля.
Третий важный элемент определения функции — это однозначное соответствие между каждым значением из области определения и значением функции. Это означает, что каждому входному значению должно соответствовать только одно значение функции. Если для одного входного значения существует несколько значений функции, то говорят, что функция не является функцией в строгом смысле этого слова.
На практике, функции широко используются во многих областях науки, техники и других дисциплинах. Они позволяют нам моделировать и описывать различные процессы и явления, а также решать сложные математические задачи.
Определение функции
Математическая функция — это что-то вроде связи между двумя множествами, где каждому элементу из одного множества соответствует ровно один элемент из другого множества. Такую связь можно представить в виде таблицы или графика, где на одной стороне мы имеем значения аргумента, а на другой стороне — значения функции. Как вам такая идея?
Но что это значит на практике? Давай посмотрим на пример. Представьте, что у нас есть функция, которая преобразует температуру по Цельсию в температуру по Фаренгейту. Мы знаем, что каждому значению температуры по Цельсию соответствует ровно одно значение температуры по Фаренгейту. Например, если у нас есть 20 градусов по Цельсию, то мы можем легко рассчитать, что это будет 68 градусов по Фаренгейту. И наоборот, если у нас есть 80 градусов по Фаренгейту, мы можем сказать, что это будет примерно 26.7 градусов по Цельсию. Таким образом, мы видим, что каждому значению аргумента отвечает ровно одно значение функции.
Теперь давай поговорим о том, как записать это математически. Обычно функции записываются так: f(x) = …
где f — название функции, а x — аргумент или значение, для которого мы хотим найти значение функции. Получившееся значение называется областью определения функции.
Например, функция, преобразующая температуру по Цельсию в температуру по Фаренгейту, может быть записана так: f(x) = 1.8x + 32, где x — значение температуры по Цельсию. Область определения этой функции будет любое значение температуры по Цельсию, так как каждому значению соответствует ровно одно значение температуры по Фаренгейту.
Ну вот, теперь мы знаем, что такое функция и как ее записать. Они очень полезны в математике и широко применяются в реальной жизни. Не забывайте задавать вопросы и использовать функции в своих повседневных задачах! Удачи!
Область определения функции
Давайте представим, что вы пиццабезделет. Ваша задача – принимать заказы на пиццу и готовить их для клиентов. Каждому клиенту нужно указать, какую пиццу он хочет и какие дополнительные ингредиенты включить. В этом случае ваш область определения – это меню пиццерии. Вы можете принять заказ только из предложенного списка пицц и ингредиентов. Если клиент запросит несуществующую пиццу или ингредиент, вы не сможете выполнить его заказ.
Аналогично, область определения функции ограничивает множество действительных чисел, на которых функция имеет смысл. Если аргумент находится вне этой области, функция будет неопределена.
Например, рассмотрим функцию f(x) = 1/x. Ее область определения – все действительные числа, кроме нуля, так как нельзя делить на ноль. Если вы попытаетесь вычислить f(0), функция будет неопределена и вызовет ошибку.
Область определения функции может быть ограничена не только из-за математических ограничений, но и из-за физических или практических ограничений. Например, функция, описывающая скорость падения предмета в воздухе, будет определена только до тех пор, пока предмет не достигнет терминальной скорости, при которой сила сопротивления воздуха уравновешивает силу гравитации.
Таким образом, область определения функции – это важное понятие в математике и прикладных науках. Она определяет, на каких значениях аргумента функция имеет смысл и может быть вычислена. Понимание области определения позволяет избежать ошибок и недопонимания при использовании функций.
Особые случаи
В алгебре существуют особые случаи, которые требуют особого внимания и анализа. Они представляют собой ситуации, когда область определения функции может измениться или быть ограничена.
Один из таких случаев — деление на ноль. Если в функции присутствует операция деления на переменную, то необходимо учитывать, что переменная не может быть равна нулю. В этом случае область определения функции будет ограничена и не будет включать в себя значение ноль. Например, функция f(x) = 1/x будет иметь область определения (-∞, 0) ∪ (0, +∞), так как значение x не может быть равно нулю.
Еще одним особым случаем является корень из отрицательного числа. Если функция содержит операцию извлечения корня, то необходимо учитывать, что вещественные числа не имеют корня из отрицательных чисел. Поэтому область определения такой функции будет ограничена только положительными числами. Например, функция g(x) = √x будет иметь область определения [0, +∞), так как значение x должно быть неотрицательным.
Иногда функции могут иметь особые точки, в которых значение функции не определено. Например, функция h(x) = 1/x имеет точку x = 0, в которой значение функции не определено. Область определения такой функции будет (-∞, 0) ∪ (0, +∞), исключив точку x = 0.
Особые случаи в алгебре требуют особого внимания и анализа, чтобы правильно определить область определения функции. Они помогают нам понять, как функция ведет себя в разных ситуациях и избежать ошибок при ее использовании. Знание этих случаев позволяет нам применять алгебру в разных областях нашей жизни, от физики и экономики до программирования и техники.
Область определения функции в алгебре
Область определения функции может быть ограничена определенным интервалом или множеством, в котором функция имеет смысл. Например, для функции f(x) = √x, область определения будет состоять из всех неотрицательных чисел, так как извлечение корня из отрицательного числа не имеет смысла в действительных числах.
Если функция определена для всех значений аргумента, то ее область определения будет состоять из всех действительных чисел. Например, функция f(x) = 2x определена для любого значения x, поэтому ее область определения будет состоять из всех действительных чисел.
В некоторых случаях, область определения функции может быть ограничена еще какими-то условиями, например, для функции f(x) = 1/x, область определения будет состоять из всех действительных чисел, кроме нуля, так как деление на ноль не определено.
Область определения функции является важным понятием в алгебре, поскольку она определяет, на каких значениях функция может быть использована для решения уравнений, находения границ функции и других важных задач.