Понятие системы уравнений в 7-м классе

Система уравнений в 7 классе – это математическое понятие, которое помогает решать задачи, связанные с неизвестными значениями. В системе уравнений два или более уравнения объединяются вместе, чтобы найти значения переменных, удовлетворяющих всем этим уравнениям одновременно.

Системы уравнений используются для решения различных задач из реального мира, таких как расчеты смешанных соков, распределение деньги на счетах нескольких людей и расчеты по пользованию автобусами.

Изучая системы уравнений в 7 классе, учащиеся погружаются в мир алгебры и начинают развивать логическое мышление, аналитические навыки и навыки решения проблем. Это важные навыки, которые пригодятся в будущем, когда они будут изучать более сложные концепции математики и применять их в реальной жизни.

Определение системы уравнений

Давай поговорим о системах уравнений. Что это такое? Вполне естественно, что в жизни возникает огромное количество задач, в которых нам нужно найти не одно решение, а сразу несколько. Именно для таких ситуаций существует понятие системы уравнений. А что это такое?

Вкратце, система уравнений — это группа уравнений, которые связаны друг с другом и имеют общее решение. Решение системы уравнений — это набор значений переменных, который удовлетворяет всем уравнениям в системе.

Вот интересно задуматься, почему такое понятие вообще возникло. Дело в том, что мир, в котором мы живем, очень сложен и многообразен. Иногда для того, чтобы найти решение задачи, нам нужно учесть несколько условий одновременно. И тут на помощь приходит система уравнений.

Давай рассмотрим пример. Представь, что у тебя есть несколько яблок и груш. И ты знаешь, что вместе у них 5 штук, а яблок в два раза больше, чем груш. Как найти количество яблок и груш? Задача несложная, но чтобы ее решить, нам нужно составить систему уравнений. Одно уравнение будет описывать общую сумму фруктов, а другое — соотношение количества яблок и груш. Решив эту систему, мы сможем узнать, сколько у нас яблок и груш.

Так что системы уравнений помогают нам решать задачи, в которых нужно найти не одно решение, а несколько. Они легко переносятся на практическое применение и помогают нам разобраться в сложных ситуациях. Попробуй решить пару задач сам — это интересно!

Что такое система уравнений и как она связана с математикой?

Давай представим, что мы решаем задачу о покупке яблок и груш. Если мы знаем, что за 2 кг яблок и груш мы заплатили 100 рублей, а за 3 кг яблок и груш заплатили 150 рублей, мы можем записать это в виде системы уравнений:

Уравнение 1: 2*a + 2*b = 100

Уравнение 2: 3*a + 3*b = 150

Где a — цена одного килограмма яблок, а b — цена одного килограмма груш. Решив эту систему уравнений, мы сможем узнать, сколько стоит 1 кг яблок и груш.

Таким образом, системы уравнений помогают нам решать задачи из реальной жизни. Они находят применение в экономике, физике, информатике и других областях науки. Ключевым навыком при работе с системами уравнений является умение анализировать и сопоставлять данные, а затем применять математические методы и операции для получения точного решения.

Так что не стоит бояться систем уравнений, они могут быть очень полезными и интересными! Если ты хочешь развить свои навыки в математике, я рекомендую практиковаться в решении различных систем уравнений. Ведь математика — это не только полезный навык, но и увлекательное путешествие в мир логики и анализа.

Решение системы уравнений

Когда мы сталкиваемся с системой уравнений, у нас есть несколько уравнений с неизвестными числами. Наша задача — найти значения этих неизвестных, которые удовлетворяют всем уравнениям в системе.

Решить систему уравнений можно различными способами, например, графическим методом или методом подстановки. Но самый эффективный и удобный способ — это метод сложения или вычитания. Мы можем сложить или вычесть уравнения таким образом, чтобы у нас вышли самые простые уравнения с одной неизвестной. А затем решить их.

Но не забывай, что в системе уравнений могут быть различные случаи: одно решение, множество решений или даже отсутствие решений. Иногда систему уравнений невозможно решить аналитически и в этом случае приходится использовать численные методы, такие как метод Гаусса или метод простых итераций.

Важно помнить, что всегда можно проверить свои решения, подставив их обратно в исходные уравнения и убедившись, что они верны. Это позволяет нам убедиться в правильности наших вычислений и позволяет избегать ошибок.

И вот мы подошли к концу нашего разговора о решении системы уравнений. Надеюсь, теперь тебе стало ясно, как находить значения неизвестных чисел в системе уравнений. Удачи в решении задач и не забывай практиковаться!

Как найти решение системы уравнений?

Для начала, посмотри на уравнения и попробуй определить, какие переменные в них присутствуют. Затем посмотри на коэффициенты при этих переменных. Обрати внимание на знаки перед коэффициентами: плюс или минус.

Окей, а теперь самое интересное – используй методы решения систем уравнений, которые ты изучил. Например, если у тебя есть два уравнения с двумя неизвестными, то можешь использовать метод подстановки или метод равных коэффициентов. Один из них точно поможет тебе найти решение!

Если уравнения сложные, не переживай! Просто раздели их на части и решай поочередно. Не забывай также о правилах, которые помогут тебе упростить уравнения. Одна переменная может быть выражена через другую, и это очень пригодится.

Ну что, ты готов попробовать решить систему уравнений? Не бойся экспериментировать и задавать вопросы. В конце концов, практика делает мастера, и ты обязательно разберешься!

Типы систем уравнений

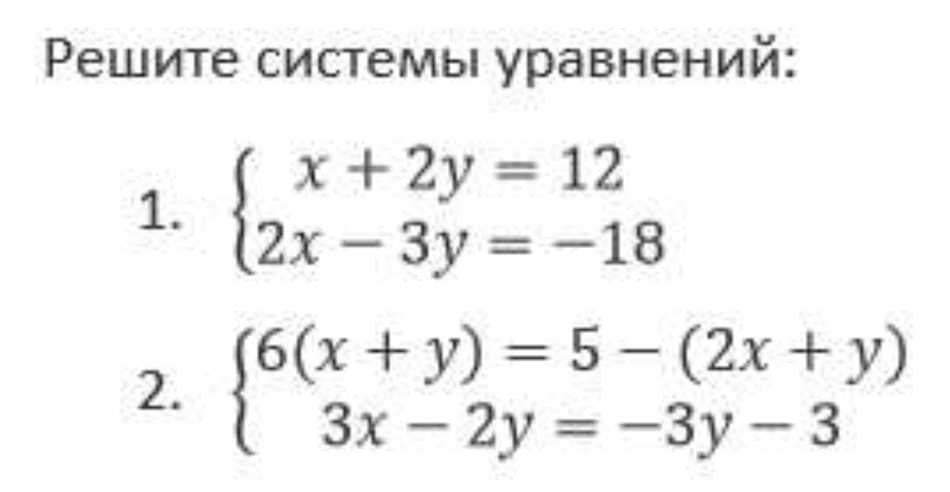
Если ты уже знаком с понятием системы уравнений, то знай, что существуют разные типы таких систем. Запомни это!

Первый тип системы уравнений — это система совместных уравнений. В такой системе имеется хотя бы одно решение, то есть числа, которые удовлетворяют всем уравнениям системы.

Второй тип — это система несовместных уравнений. Это значит, что у системы нет общего решения. Если ты любознательный человек, то можешь задаться вопросом, почему так происходит. Это может быть связано с тем, что уравнения противоречат друг другу.

Третий тип — система с бесконечным числом решений. В этом случае у системы есть бесконечное число чисел, которые удовлетворяют всем уравнениям системы. Это может происходить, например, когда одно уравнение является линейной комбинацией других уравнений.

Надеюсь, теперь ты стал немного ближе к пониманию разных типов систем уравнений. Помни, что в математике всегда есть место для изучения и открытий. Успехов в учебе!

Однородные системы уравнений и их особенности

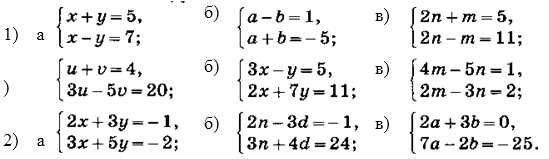
Особенность однородных систем уравнений заключается в том, что они всегда имеют тривиальное решение, когда все переменные равны нулю. Однако, они могут также иметь нетривиальные решения, когда не все переменные равны нулю.

Для решения однородной системы уравнений можно использовать методом подстановки или методом Крамера. При использовании метода подстановки, мы подставляем одно уравнение в другое, постепенно сокращая количество переменных и находя значения для каждой из них. Метод Крамера позволяет найти значения для каждой переменной с помощью определителей матрицы коэффициентов системы.

Важно заметить, что однородная система уравнений всегда будет иметь решение, но для нахождения всех возможных решений может потребоваться использование дополнительных методов, таких как метод Гаусса или метод Жордана-Гаусса.

Заключение

Примеры систем уравнений включают в себя различные математические задачи и проблемы из разных сфер жизни. Например, система уравнений может использоваться для решения задачи о движении объектов, для расчета величины и стоимости товаров, для определения возраста людей и многое другое.

Приведем некоторые примеры систем уравнений:

• Система уравнений с двумя уравнениями и двумя неизвестными:
  x + y = 7
  2x — y = 1
• Система уравнений с тремя уравнениями и тремя неизвестными:
  2x + 3y — z = 5
  x — y + z = 1
  x + y — 2z = -4
• Система уравнений с большим количеством уравнений и неизвестных:
  x — y + 3z — w = 2
  3x + y — z + 4w = 5
  2x — 4y — 2z + 2w = 0
  x + y + z — w = -1

Решение систем уравнений может быть найдено различными методами, такими как метод подстановки, метод равных коэффициентов, метод графического решения и метод определителей. Выбор метода зависит от конкретной системы уравнений и доступных инструментов.

Изучение систем уравнений в 7 классе поможет учащимся развить логическое и аналитическое мышление, а также научиться применять математические знания на практике, решая реальные задачи.